基于灾害事件的大学生集群行为防控体系的构建

吴 鹏，龙黎明

（1.四川建筑职业技术学院计算机工程系，四川德阳 618000；2.四川大学法学院，四川成都 610041）

中国是一个自然灾害频发的国家，非典型性肺炎暴发以及暴雪、洪水、干旱等灾害性事件对社会稳定的影响涉及到社会的诸多领域，特别是2008年的“5·12汶川特大地震”这样的大灾害对社会的影响更是巨大而深远。

比照突发事件，灾害事件具有不能绝对预知性、损害性、扩散性和可变性的特点［1-4］；又由于高校是一个人口密度和流动性大、青年聚集、活动频繁、极受社会关注的公共场所，这使高校大学生群体成为社会稳定工作的一个重要关注面。亲历了汶川特大地震，笔者真切地感受到灾害事件给高校政工系统带来的巨大压力，如何防控灾害事件中大学生的集群行为，既是一个值得从理论上进行探讨的问题，也具有现实的客观必要性。

1 灾害事件中大学生集群行为分析

1.1 大学生集群行为略述

集群行为是Collective Behavior的汉译词，该词也有被译为“聚合行为”或“集体行为”。集群行为是指一种在激烈的互动中自发产生、无指导、无明确目标、不受正常社会规范制约的多人的狂热行为［5］。大学生集群行为，指的是大学生这一特定社会群体所产生的集群行为。

1.2 灾害事件中大学生集群行为的特征

由于大学生群体和高校环境的特殊性，大学生集群行为较社会性集群行为具有显著不同的特征［6-7］，由于灾害这一诱发因素，大学生集群行为的特点集中体现为以下3方面。

1）偶发性

由于灾害的发生并无特别固定的规律，大学生群体中因此发生的集群行为具有明显的偶发特征。这也是给高校政工系统的相关调控工作带来巨大压力的首要因素。

2）行为的情绪化

大学生集群行为的最大特点是行为的情绪化，这在灾害事件中依然突出。由于情绪感染，大学生个体的情绪相互刺激、相互强化，降低了对客观情势的判断力，客观地导致了大学生群体情绪不稳定、不易引导。

3）行为性质转化可能性低

大学生群体的受教育程度整体上高于普通社会群体。集群行为发生后，只要大学生管理系统能继续行使职能，及时有效地进行调控，大学生们不会产生利用灾害事件造成的短时社会秩序紊乱制造事端的心态，更不可能使集群行为转化为集群犯罪。

1.3 灾害事件中大学生集群行为的具体表现形式

1）慌乱

灾害的发生，势必在一定程度、一定范围内打乱了日常生活的正常秩序。学生在灾害发生后随即出现慌乱，开始对任何可能有危险的刺激信息、物品予以高度的关注，积极地寻求暗示以逃避恐惧。

2）压抑与暴发不理智行为

在灾害发生后，出于对学生群体的保护，大学往往在条件允许的情况下把学生限制在大学校园之中。由于灾害的震撼性结果，在相对狭小、封闭的空间中，学生群体极易酝酿产生压抑的情绪，只要有一个触动因素就可能引起集群性暴发不理智行为。

3）从众

大学生在突如其来的灾害面前，置身于集群之中能给他们安全感，绝大多数学生在行动上力求与众人保持一致。譬如，在地震后相当长的一段时间内，躲避子虚乌有的“地震”的行为是最常见的集群行为。

4）无视纪律

灾后，生命的价值被无限放大，大学生群体中会出现无视纪律的小集群。比如学生无视学校的管理规定擅自离校并较长时间滞留在家。

2 灾害事件中大学生集群事件防控指标体系

据前述分析，可构建灾害事件中大学生集群事件防控指标体系（见表1）。

表1 防控指标体系Tab.1 Prevention and control system

根据对上述体系指标的分析，将指标分为3个层次以评价灾害事件中大学生集群事件发生的可能性。表1体现出了防控指标体系中的一级指标处在体系的最上层，一级指标间相互协调，共同应对集群事件。各一级下分出了多个二级指标，各二级指标之间分工明确也相互协调，各自又存在独立的明确的观测点。各观测点的选取依据则是根据学工部门的实际工作经验建立的。根据表1数据，作出以下组织结构图（见图1）。

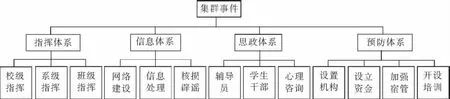
图1 组织结构图Fig.1 Organization chart

3 防控指标体系评价方法的选择

传统层次分析法（AHP）就是将人的主观判断为主的定性分析进行量化，并以数字显示各种替代方案或者各因素差异的一种系统分析方法。传统层次分析法在应用中存在如下弊端：

1）在条件复杂时不易检验判断矩阵的一致性；

2）一致性不满足时的判断矩阵的调整工作量大且难度高；

3）一致性检验的评判标准（C.R.＜0.10）缺乏科学依据。

模糊层次分析法（FAHP）［8］是针对传统层次分析法的上述不足构造出的一种改进型层次分析法，添加了模糊数学新理念，该方法在一致性检验中简单易用。为此，本文采用与传统层次分析法相结合的方式分析指标体系的各项指标。

通过对立磨机结构原理分析，结合3kW立磨机的石英砂参数确定系统最优参数，并在此条件下开展金矿选型实验，得到如下结论：

4 利用FAHP建立数学模型

4．1 模糊一致判断矩阵的建立

1）根据上述参考指标，为研究问题方便特将本系统的组织结构图表示见图2，所示是一个二级评价指标体系。

图2 组织结构图（简化后）Fig.2 Organization chart after simplified

依据如表2所示的判断尺度表，建立模糊一致判断矩阵。

表2 模糊一致判断矩阵的判断尺度表Tab.2 Judgment criterion of the fuzzy consistent judgement matrix

2）采用参考文献［9］计算各层次要素对于其上一级准则的相对重要度（权重向量），公式为

3）依据以上方法，分别建立各层的模糊一致判断矩阵，并计算权重向量，结果如下。

以A为准则，对B1，B2，B3，B4经过比较后建立的模糊一致判断矩阵如表3所示。

同理建立以Bi为准则，针对Bij（i，j＝1，2，3，4）的模糊一致判断矩阵，见表4、表5、表6和表7。

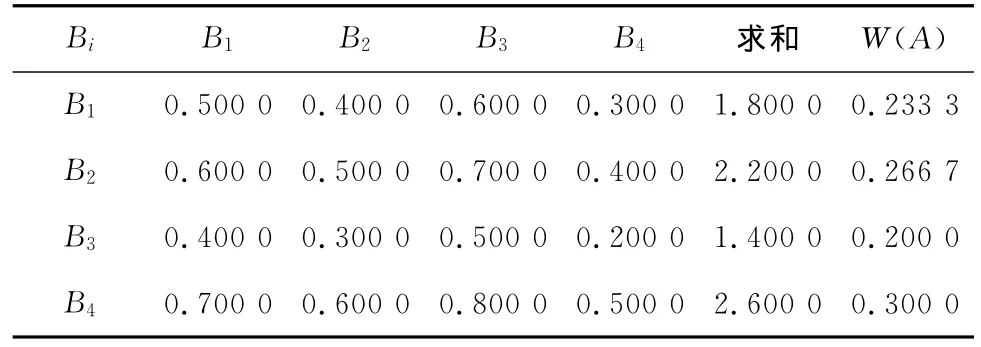
表3 A的模糊一致判断矩阵Tab.3 Fuzzy consistent judgement matrix of A

表4 B1的模糊一致判断矩阵Tab.4 Fuzzy consistent judgement matrix of B1

表5 B2的模糊一致判断矩阵Tab.5 Fuzzy consistent judgement matrix of B2

表6 B3的模糊一致判断矩阵Tab.6 Fuzzy consistent judgement matrix of B3

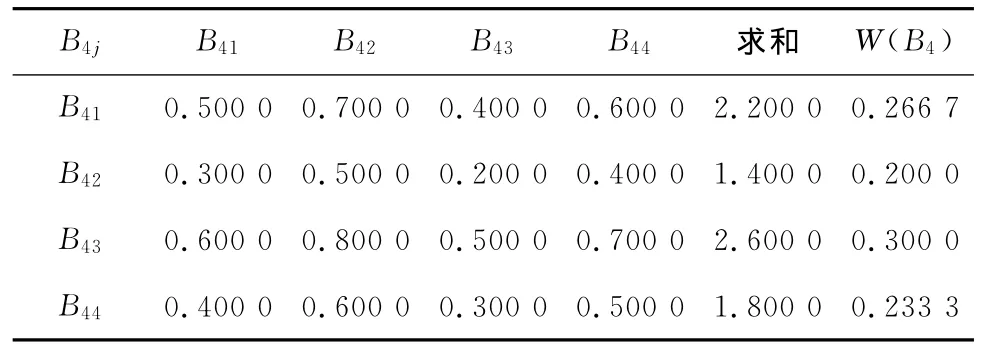
表7 B4的模糊一致判断矩阵Tab.7 Fuzzy consistent judgement matrix of B4

4.2 一致性检验

文献［8］给出了模糊判断矩阵是否具有一致性的简单方法：模糊判断矩阵中任意两行间相差一个参数。据此容易判断，表3～表7表示的判断矩阵都是通过一致性验证的。

于是表8所表示的5个相对重要度分别表示着各层因素对其上一层比较准则的权重。例如，W（B1）行的0.383 3，0.333 3，0.283 3，0.0000这4个数据分别表示着B11（校（院）级领导指挥能力）、B12（系（部）级领导指挥能力）、B13（辅导员组织能力）在突发自然灾害情况下对B1（指挥体系）发挥作用所起的影响。

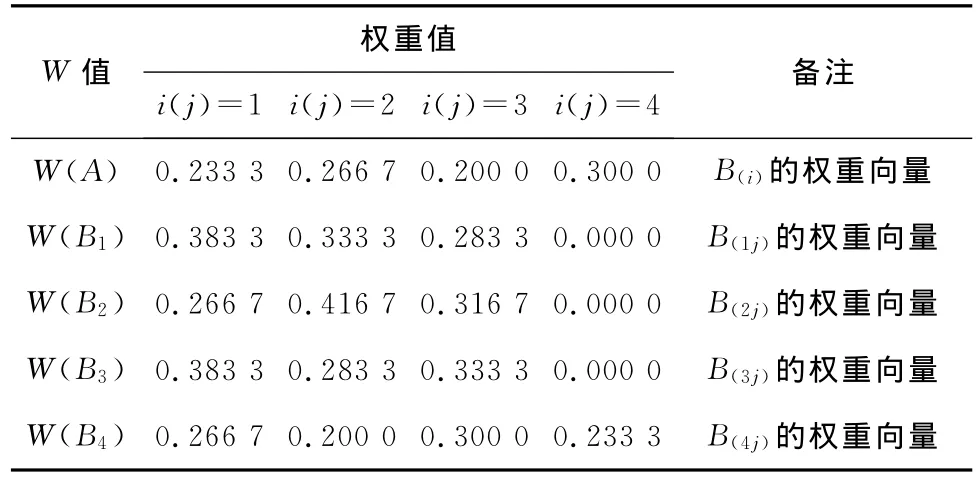
表8 权重向量Tab.8 Weight vector

另外，W（B2），W（B3），W（B4）3个一级指标下都只有3个二级指标，为分析问题方便，其第4个分量计零（0.0000）处理 。

4.3 综合重要度（综合权重）的计算

综合权重计算结果见表9。

表9 综合重要度（权重）Tab.9 Comprehensive importance

5 结果分析

综合重要度（综合权重）利用传统层次分析法所得，参看文献［10］。笔者将表9最后一列单独提出并对数据进行处理，得到整个评价体系中13个二级指标的综合排序情况，见表10。

表10 综合排序Tab.10 Comprehensive sort of index

根据此排序（综合权重）发现，在自然灾害发生或者可预见发生的时候，信息渠道所占的比例（所起作用）是最高的，在计算机普及的当今，校园中的信息交流至关重要，在预防和控制突发事件的过程中起着关键作用。占据第2位的是加强宿舍管理，因为宿舍是大学生日常生活中时间占据最多的地方，宿管员与大学生、宿管员与辅导员之间的沟通渠道也是很重要的。篇幅所限，其他权重的因素笔者就不再赘述了，读者可据此模型自行分析。

6 结 语

客观地说，四川省各高校政工系统的出色工作保证了在发生“5·12汶川特大地震”后校内没有发生不良大学生集群行为，维持了校园的稳定。以此为契机积极地进行思考和探索，通过构建该大学生集群行为防控体系，更有效地对灾害事件进行预防，将不良后果的发生率降至最低。

／References：

［1］方舟子.地震预测的梦想与现实［N］.中国青年报，2008-05-28（5）.FANG Zhouzi.Dreams and Reality of Earthquake Prediction［N］.China Youth Daily，2008-05-28（5）.

［2］叶 瑜，方修琦，葛全胜，等.从动乱与水旱灾害的关系看清代山东气候变化的区域社会响应与适应［J］.地理科学，2004，24（6）：680-686.YE Yu，FANG Xiuqi，GE Quansheng，et al.Response and adaptation to climate change indicated by the relationship between revolt and drought-flood in Shandong province during middle and late Qing dynasty［J］.Scientia Geographica Sinica，2004，24（6）：680-686.

［3］张 馨.浅析高层在建工程施工现场存在的消防安全问题及对策［J］.河北工业科技，2011，28（6）：408-410.ZHANG Xin.Analysis of high building construction site fire safety problems and countermeasures［J］.Hebei Journal of Industrial Science and Technology，2011，28（6）：408-410.

［4］刘 峥.建设单位对工程项目安全效应影响的定量分析［J］.河北科技大学学报，2011，32（3）：297-302.LIU Zheng.Construction unit＇s impact on safety effect of construction project：A quantitative study［J］.Journal of Hebei University of Science and Technology，2011，32（3）：297-302.

［5］沙莲香.社会心理学［M］.北京：中国人民出版社，2006.SHA Lianxiang.Social Psychology［M］.Beijing：Chinese People＇s Publishing House，2006.

［6］李少荣.大学生集群行为的应对与德育反思［J］.高教探索，2006（2）：84-86.LI Shaorong.Response and moral reflection cluster behavior of college students［J］.Higher Education Exploration，2006（2）：84-86.

［7］计卫舸，宋景华，周长杰.高校公共突发事件智能预警系统的设计［J］.河北科技大学学报，2012，33（2）：154-156.JI Weige，SONG Jinghua，ZHOU Changjie.Design of intelligent warning system for colleges and universities public emergencies［J］.Journal of Hebei University of Science and Technology，2012，33（2）：154-156.

［8］张吉军.模糊层次分析法（FAHP）［J］.模糊系统与数学，2000，14（2）：80-88.ZHANG Jijun.Fuzzy analytical hierarchy process［J］.Fuzzy Systems and Mathematics，2000，14（2）：80-88.

［9］姬东朝，宋笔锋，喻天翔.模糊层次分析法及其在设计方案优选中的应用［J］.系统工程与电子技术，2006，28（11）：1 692-1 694.JI Dongchao，SONG Bifeng，YU Tianxiang.FAHP and its application in the selection of design scheme［J］.Systems Engineering and Electronics，2006，28（11）：1 692-1 694.

［10］陶谦坎，汪应洛.运筹学与系统分析［M］.北京：机械工业出版社，2000.TAO Qiankan，WANG Yingluo.Operations Research and Systems Analysis［M］.Beijing：Machinery Industry Press，2000.