模n剩余类环的零因子图的补图的类数

苏华东，黄青鹤，张桂宁

(1.广西师范学院数学科学学院，广西南宁530023;2.纽芬兰纪念大学数学与统计系，加拿大 纽芬兰 A1C5S7;3.江苏科技大学数理学院，江苏镇江212003)

文中考虑的图都是简单图(没有重边和自环).图H称为图G的子图，记作H⊆G，如果V(H)⊆V(G)，E(H)⊆E(G).图G的补图，记为，满足V(¯G)=V(G)且任意2个不同的顶点在¯G是相连的，当且仅当它们在G中不相连.设集合I⊆V(G)，在I中任意2个不同顶点都没有边相连，则称I是图G的1个独立集.设v∈V(G)，G中与顶点v相连的边的数目，称为v(在G中)的度，记作deg(v).设V'⊆V(G)，导出子图G-V'，它是从G中去掉V'中的顶点及与这些顶点相连的边所得到的子图.如果V'={v∈V|deg(v)=0或1}，图G的子图G-V'称为图G的简化，记作.如果图G有2个顶点集V1，V2，使得V(G)=V1∪V2，V1∩V2=，且V1中任何1个顶点与V2中任何1个顶点是相连的，则称这个图G为完全二部图，记作Km，n，其中m=|V1|，n=|V2|.如果1个图G任何2个不同的顶点是相连的，则称这个图G为完全图，记作Kn，其中n=|V(G)|.

在球面上添加一些手柄得到了新的表面，其类数是所添加的手柄的个数.记连有i个手柄的球面为Si，其中i为非负整数.那么，Si就是类数为i的可定向曲面.图G的类数即为最小的整数m使得图G能够嵌入Sm上(也就是类数为m的可定向曲面)，记作γ(G).能够嵌入到类数为0，1，2的表面上的图分别称为可平面图、环面图和双环面图(具有2个手柄的面称为双环面).直观地说，类数代表了从球面上连出来的手柄个数.未涉及的图论定义及其它的内容可参考文献［1］.

设R是一个交换环，a∈R，若存在0≠b∈R，使得ab=0，则称a是环R的一个零因子.交换环R的所有零因子组成的集合记作Z(R)，记Z(R)*=Z(R)-{0}.设a∈R，＜a＞表示由a生成的主理想.环论中未涉及的定义请参考文献［2］.

交换环R的零因子图是一个简单图，记作Γ(R)，其顶点集为Z(R)*，2个不同的顶点a，b有边相连当且仅当ab=0.详细的定义以及Γ(R)的一些基本性质请参考文献［3］.环的零因子图已经引起了众多学者的关注［4-5］.确定一个图的类数是一个NP问题，但是由于零因子图的特殊性，可以确定一些类数较小的情形，首先在 S.Akbari等［6-7］对Γ(R)的平面性(即类数为0)进行了讨论.文献［8-10］分别确定了类数为1的零因子图，文献［11］对局部环考虑了类数为2的零因子图.当类数比较大的时候，研究起来比较困难.所以转向特殊的环类，Tang Gaohua等［12］考虑了模n高斯整数环的零因子图，确定了类数小于6的情形.模n剩余类环Zn={0，1，2，…，n-1}是个基本的有限环，A.Phillips等［13-14］研究了它的零因子图性质，包括Γ(Zn)和它的补图的中心，补图的平面性、独立集以及顶点的最小度、连通性，Γ(Zn)的核、Γ(Zn)和它的补图的顶点的着色问题等.笔者主要研究模n剩余类环Ζn的零因子图的补图的类数，通过对n的标准分解进行讨论，利用图论中已知的类数公式，采用嵌入技巧，完全确定模n剩余类环Ζn的零因子图的补图的类数不超过5的情形.

1 引理

引理 1［1］，其中{x}是指不小于x的最小非负整数.

引理 2［1］其中{x}是指不小于x的最小非负整数.

下面2个引理是显然成立的.

引理3 设图H是图G的任一子图，则有γ(H)≤γ(G).

引理4对任意简单图G，有γ(G˜)=γ(G).

引理5［1］设图G是连通图，且|V(G)|=v，|E(G)|=e，则有

引理6［1］设图G，G使得V(G)∩V(G)=

1212∅且E(G1)∩E(G2)=，记G=G1∪G2，其中V(G)=V(G1)∪V(G2)，E(G)=E(G1)∪E(G2)，则有 γ(G)=γ(G1)+γ(G2).

2 主要结果

定理1 设n=pe，其中p是素数，e≥2是正整数，则当且仅当n=p2，8，16，27.

证明 如果e=2，易知Γ(Ζp2)是1个完全图Kp-1，即是1个独立集，故下设e≥3，令

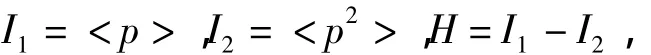
有

则对于任意a，b∈H有ab≠0，故H中任意2个不同的顶点都是有边相连的，因此如果p≥5，则

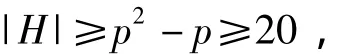
所以只需考虑p=3和p=2这2种情形.

设p=3，令

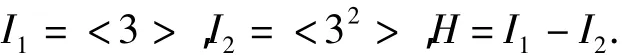
如果e≥4，则有

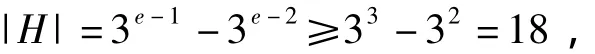
则对于任意a，b∈H有ab≠0，故H中任意2个不同的顶点都是有边相连的，从而存在1个子图是完全图K18，由引理1可得

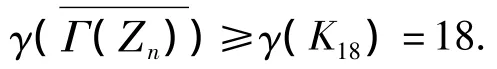
当e=3时，即n=27.令Γ(Ζ27)=G，有

其中9和18这两个点的度是0，故

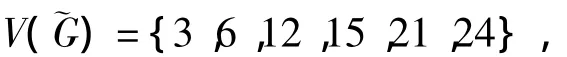
而且V)中任意2个不同的顶点是有边相连的，即˜G≅K6，由引理4和引理1，

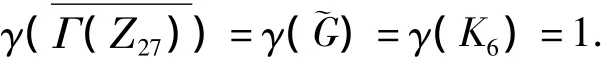
设p=2，令

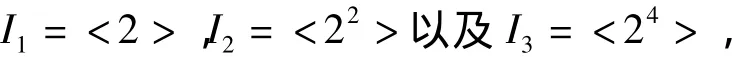
取

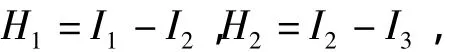
如果e≥5，则

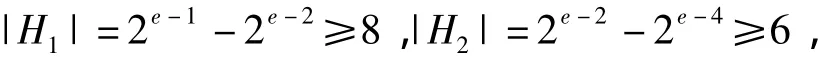
并且对于任意a∈H1，b∈H2，有ab≠0，所以H1中任意1个点与H2中任意1个点都是有边相连的，故存在一个子图是完全二部图K6，8，由引理2可得

当e=4时，设取H={2，4，6，10，14}，显然H中任意2个不同的顶点都是有边相连的，故存在1个子图是完全图K5，由引理1可得

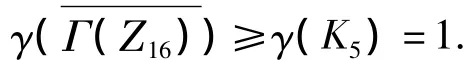
˜G在曲面S1上的嵌入如图1所示，所以

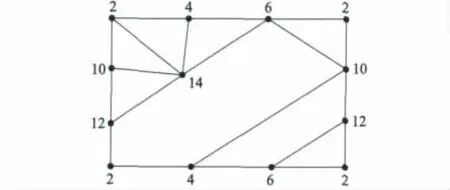
图1˜G在曲面S1上的嵌入

当e=3时，有，显然证毕.

定理2 设n=，其中:pi(i=1，2)为素数，且p1＜p2;ei(i=1，2)为正整数.则，当且仅当n=6，10，12，14，15，18，20，21，22，33，35，55，77.

证明 如果e1≥3，令

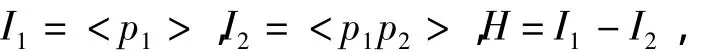
有

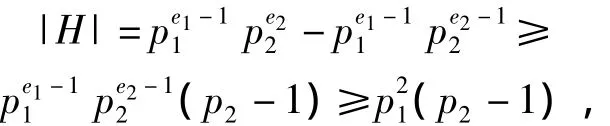
且对于任意a，b∈H有ab≠0，故H中任意2个不同的顶点都是有边相连的，因此，当n≠24时，有

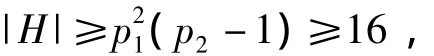
当n=24时，令，简单检验后得图G是一个连通图，且有|V(G)|=15，|E(G)|=79.

由引理5得

如果e2≥3，令

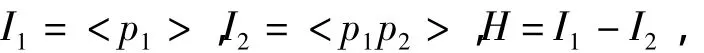
有

且对于任意a，b∈H有ab≠0，故H中任意2个不同的顶点都是有边相连的，因此Γ(Ζn)存在1个子图是完全图K18，由引理1可得

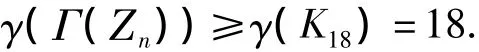
下面只需要考虑e1≤2，e2≤2的情形.

情形 1e1=e2=2，令

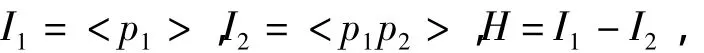
有

且对于任意a，b∈H有ab≠0，故H中任意2个不同的顶点是有边相连的，因此

存在1个子图是完全图K12，由引理1可得

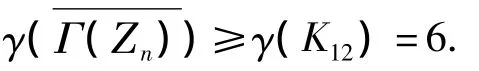
情形2e1=e2=1，即n=p1p2，此时 Γ(Zn)是完全二部图，即是2个完全图的不相交并，即

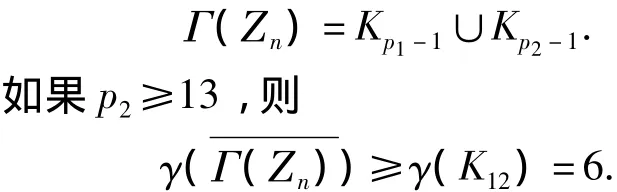
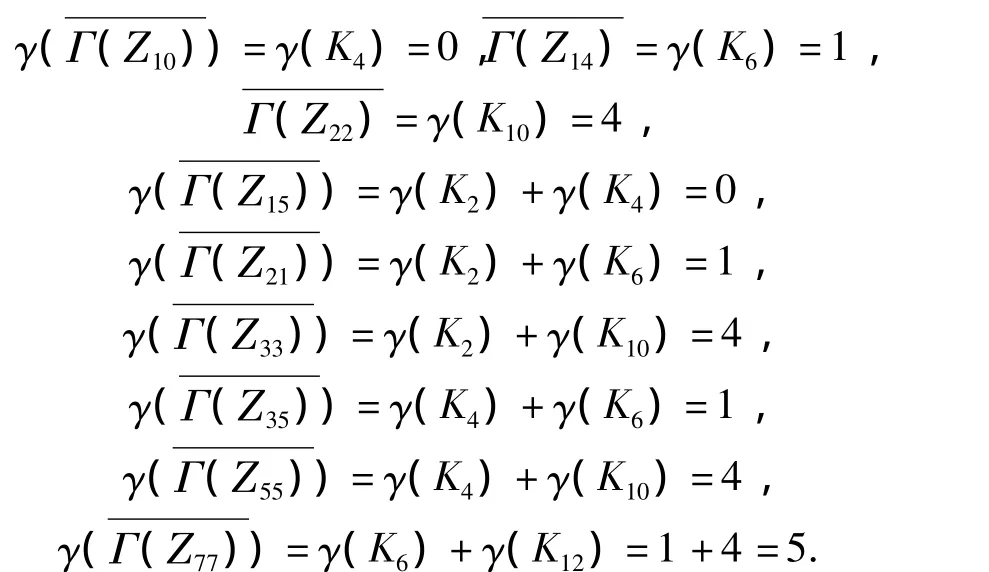
情形3e1=1且e2=2，令

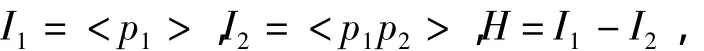
如果p2≥5，则有

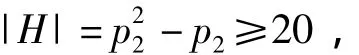
且对于任意a，b∈H有ab≠0，故H中任意2个不同的顶点是有边相连的，因此

存在1个子图是完全图K20，由引理1可得

当p1=2，p2=3即n=18时，令

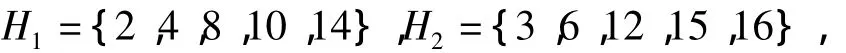
则对于任意a∈H1，b∈H2有ab≠0，故a与b是有边相连的，因此存在1个子图是完全二部图K5，5，由引理 2 可得

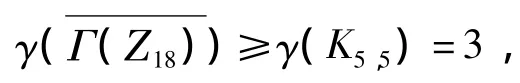
情形4e1=2且e2=1，令

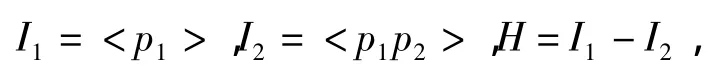
如果p2≥7则有

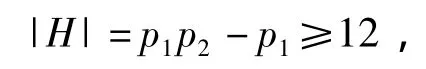
且对于任意a，b∈H有ab≠0，故H中任意2个不同的顶点是有边相连的，因此存在1个子图是完全图K12，由引理1得

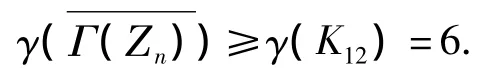
当p1=2，p2=3 时)在平面上嵌入如图3所示，故

图3 在平面上嵌入

当p1=2，p2=5时，令H=Γ(Ζ20)-10，则图H是一个连通图，且有

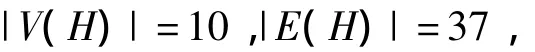
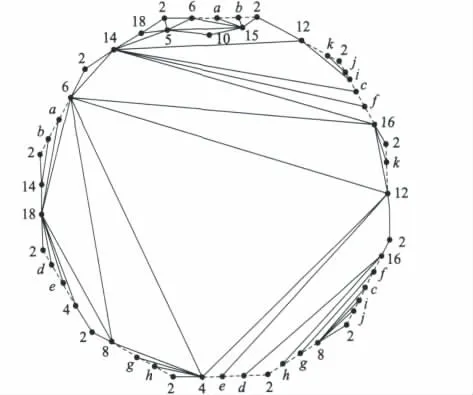
图4 在曲面S3上的嵌入

当p1=3，p2=5，取H= ＜3 ＞ - ＜15 ＞ ={3，6，9，12，18，21，24，27，33，36，39，42}，

显然H中任意2个不同的顶点是有边相连的，因此存在1个子图是完全图K12，由引理1得

证毕.

证明 当n=30 时，取H={2，3，4，6，8，9，12，14，16，18，21，22，24，26，27，28}，则|H|=16，经计算可知，H中任意2个不同的顶点是有边相连的，故存在1个子图是完全图K16，由引理1 得

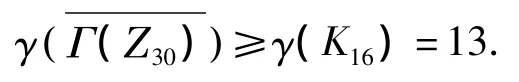
当n≠30时，构造2个理想I1=＜p1＞和I2=＜p1p3＞，取V=I1-I2，有

经验证对于任意a，b∈H有ab≠0，故H中任意2个不同的顶点是有边相连的，因此，Γ(Ζn)存在1个子图是完全图K18，由引理1得证毕.

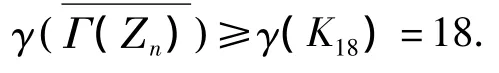
由前面的3个定理以及它们的证明过程，有如下的推论.

7)不存在n，使得

References)

［1］ White A T.Graphs，Groups and Surfaces［M］.USA:North-Holland Mathematics Studies，1984.

［2］ 唐高华.近世代数［M］.北京:清华大学出版社，2008.

［3］ Anderson D F，Livingston PS.The zero-divisor graph of a commutative ring［J］.Journal of Algebra，1999，217:434-447.

［4］ Visweswaran S.Some results on the complement of the zero-divisor graph of a commutative ring［J］.Journal of Algebra and Its Applications，2011，10(3):573-595.

［5］ LaGrange J D.Complemented zero-divisor graphs and Boolean rings［J］.Journal of Algebra，2007，315:600-611.

［6］ Akbari S，MaimaniH R，Yassemi S.When a zero-divisor graph is planar or a completerr-partite graph［J］.Journal of Algebra，2003，270:169-180.

［7］ Belshoff R，Chapman J.Planar zero-divisor graphs［J］.Journal of Algebra，2007，316:417-480.

［8］ Wang H J.Zero-divisor graphs of genus one［J］.Journal of Algebra，2006，304:666-678.

［9］ Wichham C.Classification of rings with genus one zerodivisor graphs［J］.Communications in Algebra，2008，36:325-345.

［10］ Chiang-Hsiem H J，Smith N O，Wang H J.Commutative rings with toroidal zero-divisor graphs［J］.Houston Journal of Mathematics，2010，36(1):1-31.

［11］ Bloomfield N，Wichham C.Local rings with genus two zero-divisor graphs［J］.Communications in Algebra，2010，38:2965-2980.

［12］ Tang Gaohua，Li Xiangni，Zhao Wei，et al.The genus of the zero-divisor graph ofZn［i］［J］.Guangxi Sciences，2010，17(1):8-10.

［13］ Phillips A，Rogers J，Tolliver K，et al.Uncharted territory of zero divisor graphs and their complements［D］.USA:Miami University，2004.

［14］ Cordova N I，Gholston C，Hauser H A.The structure of zero-divisor graphs［D］.USA:Miami University，2005.