数控机床单轴受力误差测量系统*
陈宝月 刘焕牢 李小力 刘 璨 谭光宇
(①广东海洋大学,广东湛江524088;②华中科技大学,湖北 武汉430074)
影响数控机床加工精度的误差因素,一般包括:机床零部件制造和装配时的几何误差(Geometric error),热变形引起的误差(Thermal Induced Error),加工过程中切削力引起的误差简称切削力误差(Cutting Force Induced Error),其他误差(如跟踪误差(Trajectory Following Error)等)[1]。经过这些年的努力,对几何误差、热误差的补偿研究已经取得了较好的成效,同时随着高性能驱动轴技术以及现代控制算法的使用,跟踪误差得以大幅度减小,然而对于切削力误差的预防和补偿却严重滞后[2-3]。各国学者在早期误差补偿技术的研究中,大部分并没有考虑切削力误差,但是,随着切削力的增大和高效切削以及一些难加工材料应用的日益广泛,切削力误差问题变得越来越突出。
Eyüp Sabri Topal等人采用测力传感器获取切削力信号,然后利用理论计算得出误差数值,对切削力误差进行测量[4]。X.Li运用神经网络建立了切削力误差模型,预测切削力分量(径向、轴向、切向)和系统变形导致的工件尺寸偏差之间的关系[5]。W.Polini[6]建立了切削力模型以预测其变形引起的工件误差。Sin-Young Lee[7]研究了数控铣床各种切削条件下的铣削力,根据刀具变形、切削力和机床误差之间的关系建立了切削力误差模型。Chana R.等人采用测力传感器间接检测切削力,使用BP神经网络建立了几何误差和力误差的综合误差模型[8]。S.Ratchev[9]、T.C.Bera[10]等通过建立铣削力模型,来预测刀具和工件变形引起的工件表面误差。
基里维斯等利用压力传感器法、电流识别法以及经验公式计算法得到力的大小,通过位移传感器获得误差数值样本[11]。吴昊等对精密车削中心切削加工过程中的热变形和切削力进行了分析,建立了热误差和切削力误差的综合模型[12]。也有通过主轴伺服电动机电流信号间接测量切削力,建立了切削力误差的神经网络数学模型[13-15]。张宏韬对双转台五轴数控机床进行了误差动态实时补偿研究,指出了五轴数控机床的几何误差、热误差和切削力误差的来源,并进行了误差的测量[16]。万敏等采用铣削力模型预测铣削误差[17]。孙暄等[18]提出一种螺旋立铣刀加工中动态切削力的建模方法,通过微元法建立的切削力数学模型和斜角等厚度切削有限元模型两者相结合,对误差的来源进行了分析。
根据以上的文献表明,在切削力和机床误差关系方面,目前主要是采用力传感器来测量切削力,通过力模型或者加工工件误差反求获取机床误差数值,都是间接地获得了切削力误差,而没有直接得到切削力和误差数值的直接对应。由于切削过程复杂,现有测量仪器不能直接用于测量切削力误差,所以目前的误差测量技术很难使用,需要采取合适的试验方法获得切削力和机床误差的对应关系。
本文针对切削力误差研究中存在的问题,模拟切削过程中工艺系统受力状态,提出数控机床单轴受力误差测量系统,直接获取机床误差(直接测量法)。
1 数控机床单轴受力误差测量系统
数控机床单轴受力误差测量系统,通过施力装置给机床施力,模拟切削过程中工艺系统受力状态,来直接测量机床误差。首先要获得施加力的大小即切削力轴向分力的大小,然后设计施加平均力(恒力)的装置,使数控机床处于或近似处于切削状态,以使步距规可以直接用于测量误差,开展“恒力”情况下的测量试验,使用步距规和杠杆式传感器的组合测量单轴受力误差,达到单轴受力和误差的直接对应。
1.1 单轴受力大小的获得
采用测力仪测量切削力,选取合适的切削参数,测量数控机床不同加工条件下的切削力大小。本文采用应变片式测力仪,是利用切削力作用在测力仪的弹性元件上,使紧贴在弹性元件上的电阻应变片随其发生变形,从而其电阻值改变,经过转换后,得出切削力各单轴分力的大小。
1.2 单轴受力误差测量系统
设计施力装置,给工作台施加恒力,模拟切削过程中工艺系统受力状态。
施力装置由定滑轮、螺纹调节机构和支架组成。钢丝绳一端连接工作台,另一端连接铁块,通过施力装置使机床受力;调整施力装置的位置,使施力方向与所测量的坐标轴共面;通过螺纹调节机构调节施力装置的高度,使施力方向与此坐标轴水平。使用步距规和杠杆式传感器的组合测量单轴受力误差(如图1)。

1.3 机床单轴受力误差的测量
采用花岗岩步距规与杠杆式传感器的组合来测量单轴受力误差。将花岗岩步距规水平地放置在机床工作台上,使用百分表进行校准(如图2),使花岗岩步距规与Y轴夹角近似等于0,在调整过程中,保证误差在10 μm 以内。

给机床X轴方向施加力,进行误差的测量,设备的连接如图1。为了减小钢丝绳与定滑轮之间在运动过程中产生的滑动摩擦,将定滑轮与钢丝绳(运动行程范围)上涂抹润滑油。调整施力装置的位置,使所施加的力与X轴水平,调整施力装置的高度,以保证力是水平的。所施力的大小由铁块的质量来决定。杠杆式传感器通过磁性座连接到主轴上,并通过RS232接口连接计算机以进行数据采集。
2 误差测量结果
在汉川机床XH714D加工中心上,运用上述机床单轴受力误差测量系统,根据所测得的切削力X轴分力的大小范围,选取0 N和140 N分别进行施力来测量误差,位置误差测量结果如表1,重复定位精度R和定位精度A结果如表2。
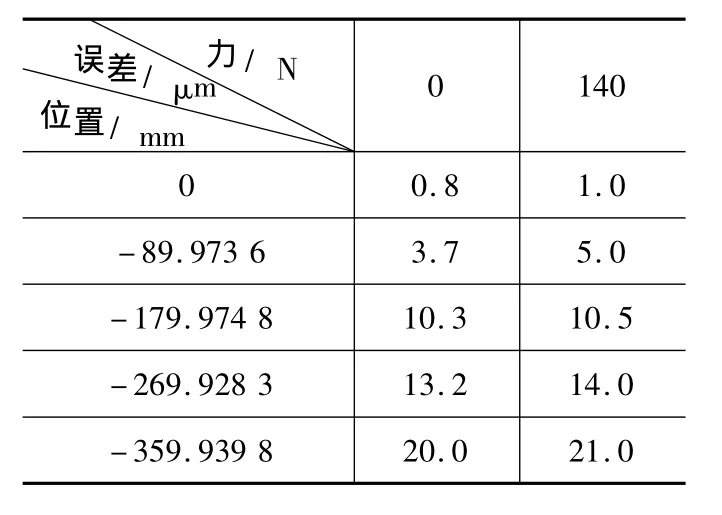
表1 位置误差测量结果
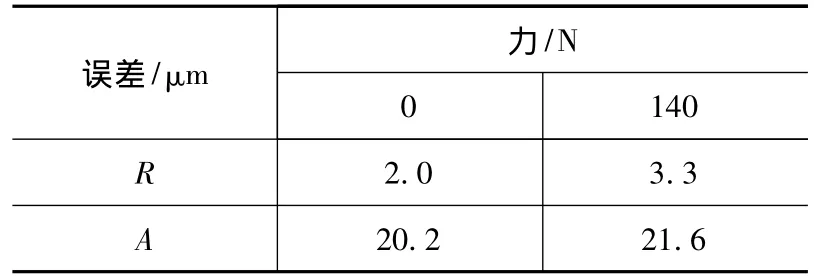
表2 重复定位精度R和定位精度A结果
3 结语
实验结果表明,数控机床单轴受力误差测量系统可以直接获得力大小与误差数值的对应;由表1、2看出,机床受力的情况下,误差数值增大,说明数控机床零部件在一定弹性变化范围内,机床单轴受力使机床的误差增大。
本文提出数控机床单轴受力误差测量系统,并测量了机床单轴受力引起的误差,实现了机床单轴受力大小和误差数值的直接对应。为数控机床单轴受力误差提供了理论基础和测量方法,为数控机床的动态特性及接触刚度提供试验数据和理论基础。
[1]Ramesh R,Mannan M A,Poo A N.Error compensation in machine tools-a review:part I:geometric,cutting-force induced and fixture- dependent errors[J].International Journal of Machine Tools& Manufacture,2000,40(9):1235 -1256.
[2]Ramesh R,Mannan M A,Poo A N.Error compensation in machine tools - a review:Part II:thermal errors[J].International Journal of Machine Tools& Manufacture,2000,40(9):1257-1284.
[3]Schwenke H,Knapp W,Haitjema H,et al.Geometric error measurement and compensation of machines- An update[J].CIRP Annals -Manufacturing Technology,2008,57(2):660 -675.
[4]Eyüp Sabri Topal,Can C.A cutting force induced error elimination method for turning operations[J].Materials Processing Technology,2005,170(1/2):192 -203.
[5]Li X.Real-time prediction of workpiece errors for a CNC turning centre,Part 4.Cutting- Force- Induced Errors[J].International Journal of Advanced Manufacturing Technology,2001,17(9):665 -669.
[6]Polini W,Prisco U.The estimation of the diameter error in bar turning:a comparison among three cutting force models[J].Int J Adv Manuf Technol,2003,22(7/8):465 -474.
[7]Sin-Young Lee,Jang Moo Lee.Specific cutting force coefficients modeling of end milling by neural network[J].KSME International Journal,2000,14(6):622-632.
[8]Chana R,Manukid P.Geometric and force errors compensation in a 3-axis CNC milling machine[J].International Journal of Machine Tools and Manufacture,2004,44(12/13):1283 -1291.
[9]Ratchev S,Liu S,Huang W,et al.An advanced FEA based force induced error compensation strategy in milling[J].International Journal of Machine Tools& Manufacture,2006,46(5):542-551.
[10]Bera T C,Desai K A,Rao P V M.Error compensation in flexible end milling of tubular geometries[J].Journal of Materials Processing Technology,2011,211(1):24 -34.
[11]基里维斯,杨建国,吴昊.切削力误差混合补偿系统[J].南京航空航天大学学报,2005,37(增刊):118 -120.
[12]吴昊,杨建国,张宏韬.精密车削中心热误差和切削力误差综合建模[J].四川大学学报:工程科学版,2008,40(2):165 -169.
[13]陈志俊.数控机床切削力误差建模与实时补偿研究[D].上海:上海交通大学,2008.
[14]吴昊,基里维斯,赵海涛,等.基于电流测量的数控机床切削力误差建模与实时补偿[J].机械制造,2005(8):13-15.
[15]周文彬.基于FANUC 0i MC的数控机床补偿研究[J].制造技术与机床,2010(3):115-117.
[16]张宏韬.双转台五轴数控机床误差的动态实时补偿研究[D].上海:上海交通大学,2011.
[17]万敏,张卫红.铣削过程中误差预测与补偿技术研究进展[J].航空学报,2008,29(5):1340 -1349.
[18]孙暄,安庆龙,张东进,等.立铣加工动态切削力预测新方法及应用[J].机械设计与研究,2008,24(3):84 -88.

