基于模糊隶属函数的参数稳健估计

王永弟，丁海勇，罗海滨

（1.南京信息工程大学 遥感学院，江苏 南京 210044）

线性模型最小二乘估计是线性最优无偏估计，这一结论是在假设观测值服从正态分布的前提下得到的，但在实际中，由于观测量中往往不可避免地存在粗差，因此，正态分布的假设前提不再成立，即观测值遭受粗差污染时，最小二乘估计不具有抵抗粗差干扰的能力，单个观测值的偏差也可能导致最小二乘估计面目全非[1]。为了解决这个问题，数理统计学家们提出了具有抵抗粗差能力的稳健估计。稳健估计是假设观测值服从污染分布的前提下，通过牺牲最优性来达到抵抗粗差的目的。在实际的参数估计过程中，人们一般不是选用最小二乘估计，就是选用稳健估计，由于不知道观测值究竟服从什么分布，所以不论选用哪种估计，都要担很大的风险[2]。利用模糊逻辑关系构建抗差估计解，能取得满意的结果。为此中国学者建立了观测误差与残差的模糊逻辑关系以及观测误差属于粗差的隶属函数，提出了顾及模糊逻辑关系的抗差估计算法[3，4]。另一方面，现实中的模型往往并不是线性模型，而是非线性模型，用线性模型的理论来处理非线性模型，只是一种简单的、近似的方法，不可避免地会引起模型误差[5]。

本文利用模糊隶属函数，通过隶属度加权来削弱个别异常数据对参数估计结果的影响，从而在不影响最优性的前提下达到提高参数估计稳健性的目的。在进行数据处理前，无需考虑观测值究竟服从什么样的分布，也无需考虑模型本身是否为线性模型，只需要利用模糊隶属函数进行定权，然后再按照定权结果进行加权最小二乘运算，即可得到满意的结果。

1 模糊隶属函数简介

模糊集合定义如下：论域U上的模糊子集A是指对于任何x∈U都有一个数 与之对应，即

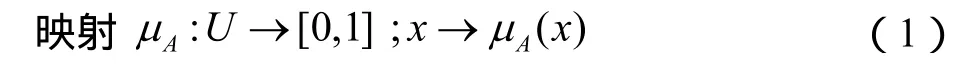
映射μA称为A的隶属函数，μA(x)表示元素x属于A的程度，称为x对A的隶属度。

模糊子集由其隶属函数所确定。隶属函数是普通集合中特征函数的推广[6]，是模糊数学中最为基本的概念，模糊集合完全由其隶属函数决定。应用模糊数学解决实际问题时，隶属函数的确定非常重要。合理地确定隶属函数将更能反映模糊概念的本质，包含更多的信息[7]。确定隶属函数的方法主要有模糊统计法、三分法、增量法等[8]。常用的隶属函数有B样条隶属函数、高斯隶属函数等，Matlab 软件模糊逻辑工具箱内置的隶属函数有11种（主要由分段线性函数、高斯分布函数、S形曲线、二次和三次多项式曲线等基函数构成），本文选取高斯隶属函数、三角形隶属函数和钟形隶属函数进行了实验。

2 模型简介

2.1 模型的建立

设不同精度独立观测值为L=(L1L2…Ln)T[9]，相应的权矩阵为P=diag(p1p2…pn)，其误差方程为：

其纯量形式为：

式中，f既可以是线性函数，也可以是非线性函数。

相应的权为pi，根据隶属度可作为权重的原理，权值pi可以由模糊隶属函数按式（4）确定：

式中，μ(vi)即为模糊隶属函数。于是，将pi也表示成误差vi的函数，则求解误差方程的准则可转化为求加权最小二乘：

将式（3）代入式（5）进行求解，本文选择迭代算法中收敛快、运算量较小的高斯-牛顿法或改进的高斯-牛顿法进行迭代运算，2种迭代都可以得到满意的结果。

2.2 模糊隶属函数的选择

对于式（4）、式（5）中μ(vi)的确定，本文选取了3个隶属函数：高斯曲线隶属函数、三角形隶属函数和钟形隶属函数（如图1～图3所示）。

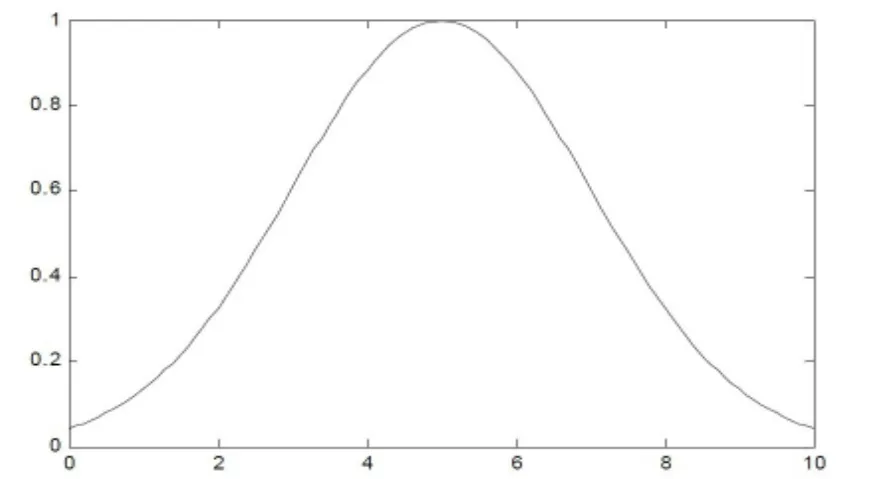
图1 高斯隶属函数

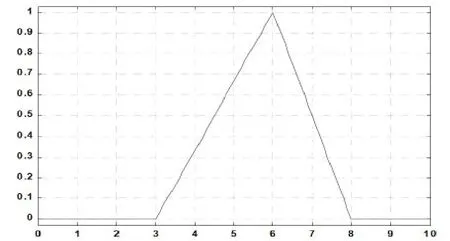
图2 三角形隶属函数

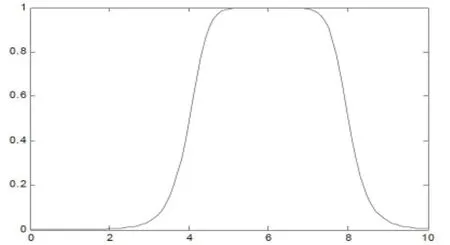
图3 钟形隶属函数

1）高斯隶属函数，其表达式为：

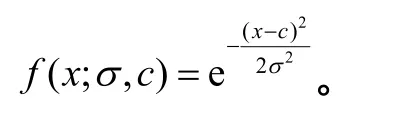
2）三角形隶属函数，其表达式为：

3）钟形隶属函数，其表达式为：

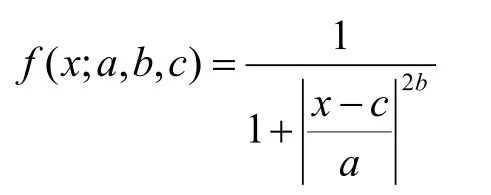
其中，定义域由向量x确定，曲线形状由参数σ、a、b、c确定。

隶属函数曲线形状较尖，则敏感性和快速性好，但稳定性较弱；形状平缓，敏感性和快速性差，但可以改善系统的稳定性。曲线型隶属函数与概率分布函数接近，有较好的准确性，直线型的隶属函数准确性较差，但计算简单快速[10]。在以上3种模糊隶属函数中，三角形隶属函数既有较高的敏感性和快速性，也具有计算简单、快速的特点，是一种比较实用的隶属函数。

在进行数据处理时，事先并不清楚观测值是否服从正态分布，这样，在判断数据是“正态分布”或“非正态分布”过程中带有一定的模糊性。因此，可以利用实测数据隶属度的计算公式进行区分，建立以该隶属度为权重的参数稳健估计模型。该模型通过隶属度加权来削弱个别粗差污染数据对参数估计结果的影响，从而达到提高参数估计稳健性的目的。

由于基于模糊隶属函数的参数稳健估计兼有最小二乘估计和稳健估计的优点，所以，当观测值服从正态分布时，该模型和最小二乘估计一样，是未知参数的最优无偏估计。当观测值含有粗差，不服从正态分布时，该模型具有很好的抵抗粗差的能力。

3 实例应用

针对线性与非线性模型2种情况，通过下面2个实例分别进行计算和比较，并讨论基于模糊隶属函数的参数稳健估计的抗差性能。

3.1 线性模型

实例1：某回归问题的自变量取值xi和观测值yi的数据如表1，求回归方程（本例取自文献[11]中的例 1）。

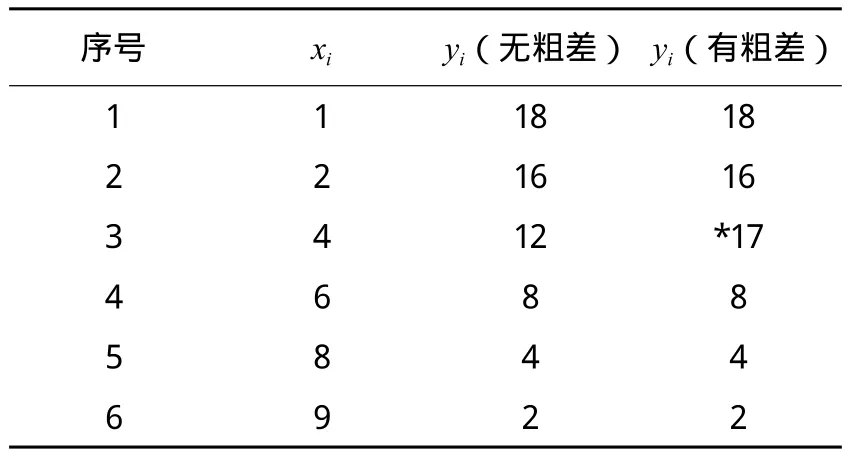
表1 观测数据

由表2可知，当观测值中不含粗差时，利用3种模糊隶属函数进行定权都可以取得与普通最小二乘法基本相同的结果；而当观测值中加入粗差（x3=4，y3=17）时，普通的等权最小二乘计算结果明显变差（Δ=1.317 618），而其余方法结果（Δ=0.193 926、0.000 026、0.000 040）均明显好于普通最小二乘法。

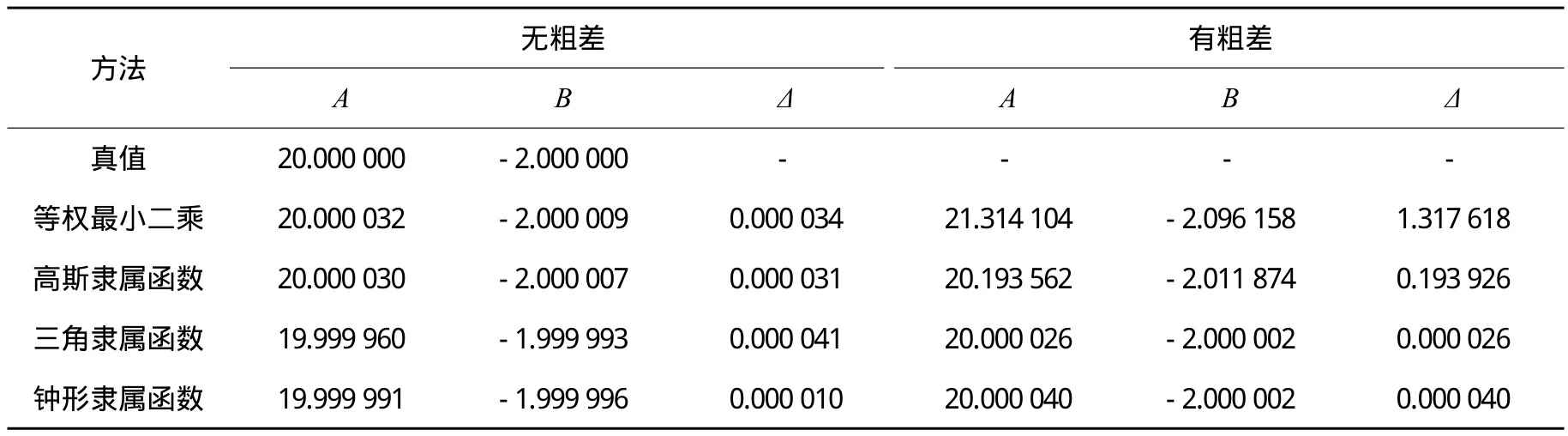
表2 计算结果

3.2 非线性模型

实例2：本例取自文献[9]第32页中的例2-1-1。已知非线性模型为Li=x1eix2，其中参数x1和x2的真值为X=(5.420136187-0.25436189)T，Li的5个真值（用参数的真值X算得）和相应的5个同精度独立观测值列于表3。

表3 原始数据

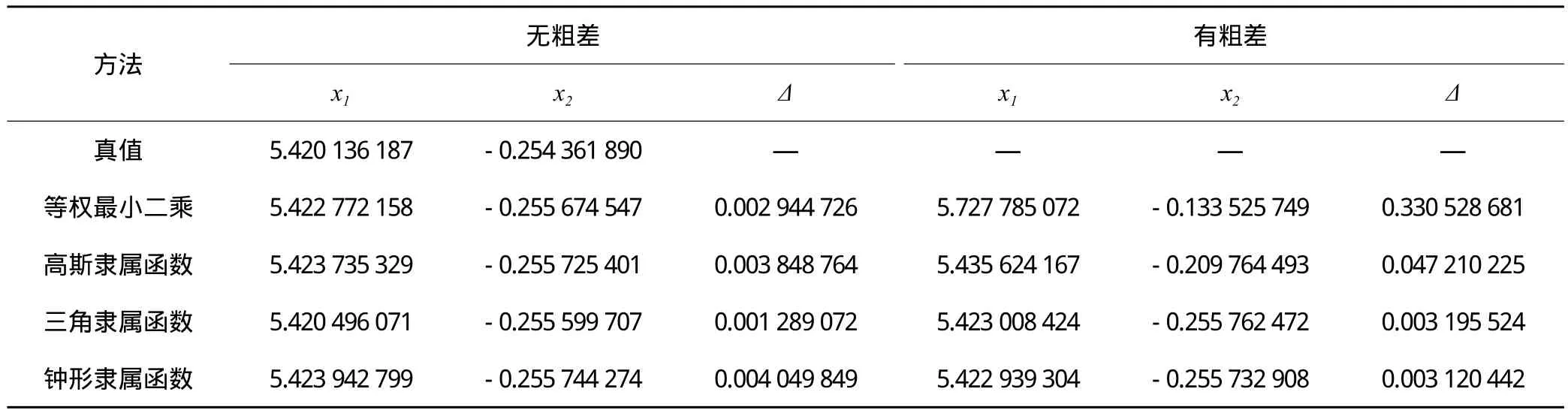
表4 计算结果

由表4可知，当观测值中不含粗差时，利用3种模糊隶属函数进行定权都可以取得与普通最小二乘法基本相同的结果；而当观测值中加入粗差（L3=8.52）时，普通的等权最小二乘计算结果明显变差（Δ=0.330 528 681），而其余方法结果（Δ=0.047 210 225、0.003 195 524、0.003 120 442）均明显好于普通最小二乘法。

4 结 语

当观测值不服从正态分布时，最小二乘法具有明显的负面影响，稳健估计能达到抵抗粗差的目的，却是以牺牲最优性为代价。另外，非线性模型参数估计进行线性近似处理时，模型误差会导致对粗差的错误鉴别和定位。针对上述问题，本文使用模糊隶属函数对观测值进行了动态定权。该模型通过隶属度加权来削弱个别异常数据对参数估计结果的影响。在进行数据处理前，无需考虑观测值究竟服从什么样的分布，也无需考虑模型本身是否为线性模型。本文以实例进行计算分析，结果表明：①基于模糊隶属函数的参数稳健估计是一种抗差性能良好的稳健估计，当观测值服从正态分布时，能够达到最小二乘的最优无偏效果；当观测值含有粗差而不服从正态分布时，不仅能很好地抵抗粗差，而且能得到最优效果；②基于模糊隶属函数的参数稳健估计不但适用于线性模型，而且适用于非线性模型。

[1]杨元喜.抗差估计理论及其应用[M].北京：八一出版社，1993

[2]王新洲.基于信息扩散原理的估计理论、方法及其抗差性[J].武汉测绘科技大学学报，1993（3）：240-244

[3]王新洲.顾及模糊逻辑关系的稳健估计[J].武汉测绘科技大学学报，1996，21（4）：338-343

[4]杨元喜，张丽萍.中国大地测量数据处理60年重要进展（第二部分）：大地测量参数估计理论与方法的主要进展[J].地理空间信息，2010（1）：1-6

[5]周江文.经典误差理论与抗差估计[J].测绘学报，1989（2）：115-120

[6]王新洲，史文中，王树良.模糊空间信息处理[M].武汉：武汉大学出版社，2003

[7]刘小艳，刘欣宇，王梅.隶属函数的确定及应用[J].电脑知识与技术，2010（31）：8 831-8 832

[8]张国良，曾静，柯熙政，等.模糊控制及其MATLAB应用[M].西安：西安交通大学出版社，2002

[9]王新洲.非线性模型参数估计理论与应用[M].武汉：武汉大学出版社，2002

[10]余琼芳，陈迎松.模糊数学中隶属函数的构造策略[J].漯河职业技术学院学报：综合版，2003（1）：12-14

[11]黄洪钟，关立文，吴海帆，等.模糊加权线性回归模型及其在S-N曲线回归分析中的应用研究[J].机械设计，2000（10）：11-12，29