多约束条件下多类保障设备配置优化模型

文 佳

(中国西南电子技术研究所,成都610036)

1 引 言

保障设备是装备使用与维修保障过程中不可或缺的保障资源,其部署数量的多少直接影响保障效能的发挥进而影响到装备的战斗力水平。在研制阶段,由于保障系统尚未部署,保障方案尚未物化,此时调整保障设备的配置数量相对使用阶段更加容易。在工程实践中,研制阶段保障设备的配套数量主要根据工程经验或参照相似装备保障设备的配套比来确定[1],往往与实际所需数量存在较大的差别,存在配置过多或过少的情况。保障设备过量配置会增加保障系统的规模,使得保障系统转场困难,同时会增加保障设备的采购费用及其使用与维护费用,使保障系统的经济性差[2];保障设备配置过少则会导致装备的使用和维修保障需求不能得到及时有效的满足,降低装备的战备完好性和任务持续性水平[3]。因此,有必要在研制阶段对保障设备的配置数量进行优化,使之在满足装备使用与维修保障需求的条件下,兼顾保障系统的部署性和经济性要求,提高保障系统的配置效率[4-5]。

目前,国内外对于保障设备数量优化方法的研究不少,现有的优化模型一般将保障站点内的保障设备服务过程视为随机服务过程,选择保障设备的等待时间或利用率作为服务系统的评价指标,有的模型还会考虑保障设备费用、体积或重量的限制,然后运用排队论理论来建立评价指标与保障设备配置数量之间的函数关系,最后采用边际效应法求解优化结果[6-10]。这类模型的缺点在于将保障站点内各种保障设备分开考虑,单独对每种保障设备进行优化,无法达到保障站点内各类保障设备配置整体最优的效果。此外,虽然已有对保障设备满足率指标的研究[11-12],但并未有文献将其考虑到保障设备配置优化模型中。

基于以上现状,本文引入保障站点平均保障设备满足率作为优化目标,以平均保障设备利用率的均值和方差、保障设备总费用和保障设备规模作为联合约束条件,综合考虑保障系统的可用性、经济性和部署性要求建立保障设备配置数量联合优化模型。且针对该模型约束条件不唯一、优化目标函数为复杂非线性函数的特点,采用AGA算法对其进行求解[13]。

2 建模分析

2.1 维修保障过程分析

二级维修体制下航空装备维修保障流程如图1所示,装备故障后在装备外场站点通过更换外场可更换单元(Line Replaceable Unit,LRU)或外场可更换模块(Line Replaceable Module,LRM)进行修复,更换下来的故障LRU/LRM送到基地级站点进行修复。在外场或基地级站点内,当故障产品(装备、LRU或LRM)到达时,根据故障模式的不同选择相应的维修保障活动及其对应的保障设备,若所需的保障设备空闲,则开始维修活动,否则进入等待队列。假设故障产品在站点内等待队列接受维修保障服务按照先到先服务(FCFS)原则进行,各级保障站点内的保障设备可以看作一个服务系统,站点内保障设备的服务过程是典型的随机服务过程,可采用排队论进行研究。

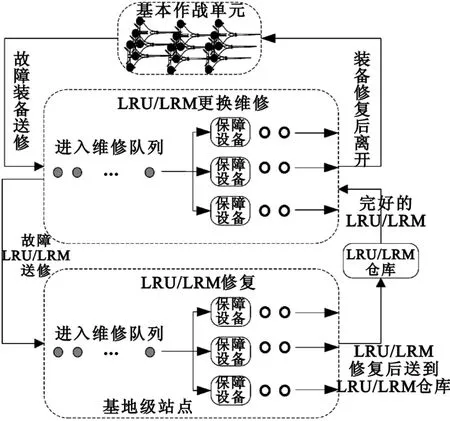
图1 二级维修体制下装备维修保障流程Fig.1 Two-level maintenance support process

2.2 优化目标与约束条件分析

要建立保障设备配置优化模型,需选择合适的指标参数来反映保障设备满足维修保障需求好坏的程度。由前面的维修保障过程分析可知,保障设备的服务过程可视为典型的随机服务过程,因此,可以选择保障设备满足率和利用率作为评价指标。

保障设备满足率是指保障活动到达保障站点时不用等待保障设备,能够马上开始的概率,反映了保障设备的配置数量对于保障活动及时开始的影响。保障设备利用率是指在规定的条件下和规定的时间内保障设备被利用的概率,反映了保障系统的运行效率。结合保障设备满足率与利用率能反映保障设备配置数量对于保障系统的资源配置效率的影响。在进行保障站点内的所有保障设备配属数量的联合优化时,一般选择保障设备满足率作为优化目标,同时将保障设备利用率作为约束条件。

同时,在能获取站点内保障设备体积、重量以及费用等数据的前提下,还可以将保障设备规模和总费用作为联合约束条件,与保障设备利用率一起使用,以满足保障系统的部署性要求和经济性要求。

3 优化模型建立

由建模分析可以建立以站点内平均保障设备满足率为目标,以保障设备规模、保障设备总费用、保障设备利用率的均值和方差作为联合约束的保障设备配置优化模型,其数学表达式如下:

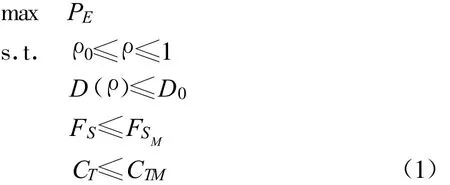
式中,PE表示站点内平均保障设备满足率函数;ρ与ρ0分别表示保障设备利用率均值的函数与最小值;D(ρ)与D0分别表示保障设备利用率方差的函数和最大值;FS与FSM分别表示保障设备规模的函数与最大值,FS由站点内保障设备的总重量与总体积以及选择的运输工具决定;CT与CTM分别表示保障设备总费用的函数与最大值。

在工程实践中,用户可以根据自己的需求和当前现有的数据情况对约束条件进行适当的放松。例如,在进行基地级站点保障设备配置优化时,可放开保障设备规模约束;当费用数据不足时,可放开保障设备费用约束。

3.1 保障设备满足率计算

3.1.1 站点级平均保障设备满足率计算

平均保障设备满足率是指保障站点内所有保障活动的保障设备满足率的均值,可由保障站点内所有保障活动的保障设备满足率按其频率加权计算得到,表达式如下:

式中,D表示保障站点内所有保障活动的频率矩阵,D=(f1,f2,…,fi,…,fn);fi表示第i项保障活动的发生频率;n表示外场站点内保障活动集合中元素的数量;PE表示保障站点内保障活动的保障设备满足率矩阵,PE=(PE1,PE2,…,PEi,…,PEn)T;PEi表示第i项保障活动的保障设备满足率;E是1×n阶矩阵,E=(1,1,1,…,1);“＊”是卷积乘号。

3.1.2 保障活动的保障设备满足率计算

由于执行一项保障活动过程中可能需要使用到一种或多种保障设备,同时,一种保障设备也可能被一项或多项保障活动使用,因此,保障活动与保障设备的关系包括4种:1∶1、1∶N 、N∶1和 N∶M。当保障活动与保障设备之间关系为1∶1或1∶N时,一个保障设备只可能被一项保障活动使用,不需要考虑不同项保障活动共同占用同一保障设备对保障设备满足率的影响;当保障活动与保障设备之间关系为N∶1或N∶M时,需要考虑不同项保障活动共同占用对于保障设备满足率的影响。

根据保障活动与保障设备之间的关系,按照是否考虑不同项保障活动共同占用同一保障设备对保障活动保障设备满足率的影响,给出下面3类保障活动的保障设备满足率计算方法。

(1)保障活动与保障设备之间关系为1∶1和1∶N

当保障活动与保障设备之间关系为1∶1和1∶N时,保障设备的服务过程可以看作一个多服务台排队系统或单服务台系统,记作

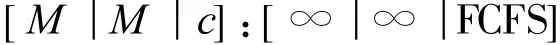
其中,c表示服务台数量,计算公式为

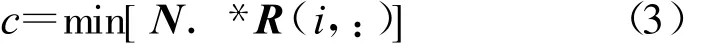
式中,N=(N1,N2,…,Nj,…,Nm)表示站点内保障设备配置数量矩阵;Nj为保障设备Ej的配置数量;m为站点内配置的保障设备种数;R表示保障活动与保障设备关系矩阵,R=[rij]n×m;若保障设备j被保障活动i使用,则 rij=1,否则,rij=0;R(i,:)表示 R中第i行所有元素;“.＊”是点乘符号,表示两个矩阵中对应位置的元素两两相乘。

保障活动的保障设备满足率的计算公式为

式中,μi为保障活动i的服务速率。

(2)保障活动与保障设备之间关系为N∶1

当保障活动与保障设备之间关系为N∶1时,由保障活动与保障设备关系矩阵R可以找到保障活动i需要的保障设备Ej。对于保障设备Ej,其保障活动的到达频率(λ)和服务速率(μ)的计算过程如下:

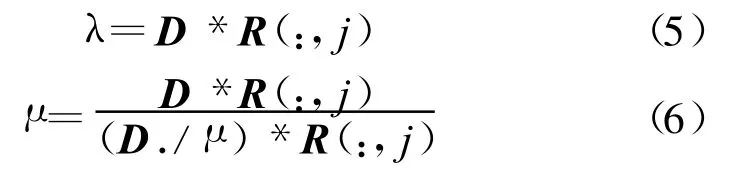
式中,R(:,j)为保障活动与保障设备关系矩阵R中第j列所有元素;μ为站点内保障活动的服务速率矩阵 ,μ=[ μ1,μ2,μ3,…,μn];“ ./”是点除符号,表示两个矩阵中对应位置的元素两两相除。

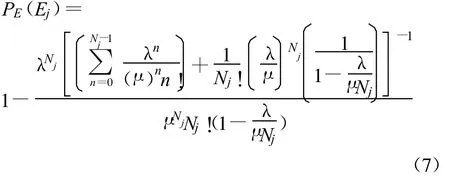
保障设备Ej的服务过程是典型的排队系统服务过程,可视为一个多服务台排队系统或单服务台系统,其对应保障设备满足率的计算公式为

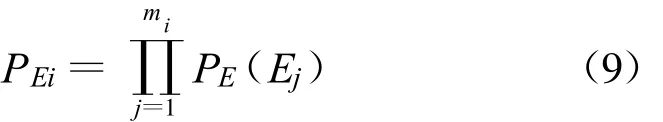
3.2 保障设备利用率均值与方差计算

保障设备利用率的均值反映了保障站点内所有保障设备的平均使用情况,可由站点内各类保障设备利用率按其占有比例加权计算得到,表达式如下:

保障活动i的保障设备满足率等于保障设备Ej的满足率,故有

式中,PE(Ej)为保障设备 Ej的满足率,其计算见公式(7)。

(3)保障活动与保障设备之间关系为N∶M

当保障活动与保障设备之间关系为N∶M时,由保障活动与保障设备关系矩阵可以找到保障活动i使用到的保障设备组,记为E=(E1,E2,…,Ej,…,Emi),其中,mi表示保障活动i所需的保障设备组中保障设备种数;Ej为保障设备组中第j个保障设备。

对保障活动i的服务过程进行分析可知,当保障活动i到达保障站点时,若其所需的保障设备组中每类保障设备都有处于空闲可用状态的设备,则保障活动i进入服务状态,否则进入排队队列进行等待。只有当保障设备组中每类保障设备都有处于空闲可用状态的设备时,保障活动 i才开始执行。因此,保障活动i相当于在mi个不同类型的服务台进行排队,保障活动i的保障设备满足率为在mi个队列中不需要等待的概率,故保障活动i的保障设备满足率等于保障设备组中每个保障设备满足率的乘积:

式中,ρ为站点内保障设备利用率矩阵,ρ=[ρ1,ρ2,…,ρj,…,ρm];ρj表示保障设备Ej的利用率,其计算公式为

保障设备利用率的方差用来度量每个设备保障设备利用率和其均值之间的偏离程度,其计算公式为

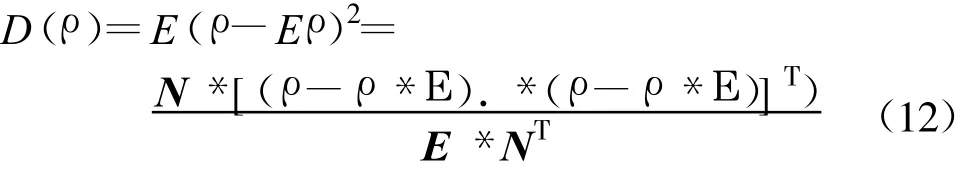
保障设备利用率的方差越大,表明站点内保障设备的使用程度越不均衡,在进行保障设备配置时,应尽量减小保障设备利用率的方差,使各类保障设备都得到合理充分的使用。

4 模型求解

由保障设备满足率与利用率模型可知,本文建立的优化模型中决策变量之间是复杂的非线性关系,无法采用传统的优化算法进行求解。考虑到自适应遗传算法在解决复杂非线性目标函数优化上的优势及其优异的全局搜索能力和局部搜索能力,本文选择自适应遗传算法作为优化模型的求解算法。

AGA算法求解的具体过程见文献[14],本文不再赘述。值得注意的是,在算法的程序设计时,需注意一些隐含约束,以减少程序的搜索空间,提高求解速度和效率。例如,由单个保障设备利用率约束(0<ρj<1)以及保障设备规模和总费用约束可以得到保障设备Ej配置数量的取值范围:

式中,MS与VS分别表示标准集装箱的最大载重和最大容积,Mj与Vj分别表示保障设备Ej的包装重量与包装体积,CEj为保障设备Ej的单价,‖‖表示取整符号。

5 案例分析

某通信导航识别子系统包括2个LRU和4个LRM,其外场的维修保障活动及所需保障设备数据如表1所示。

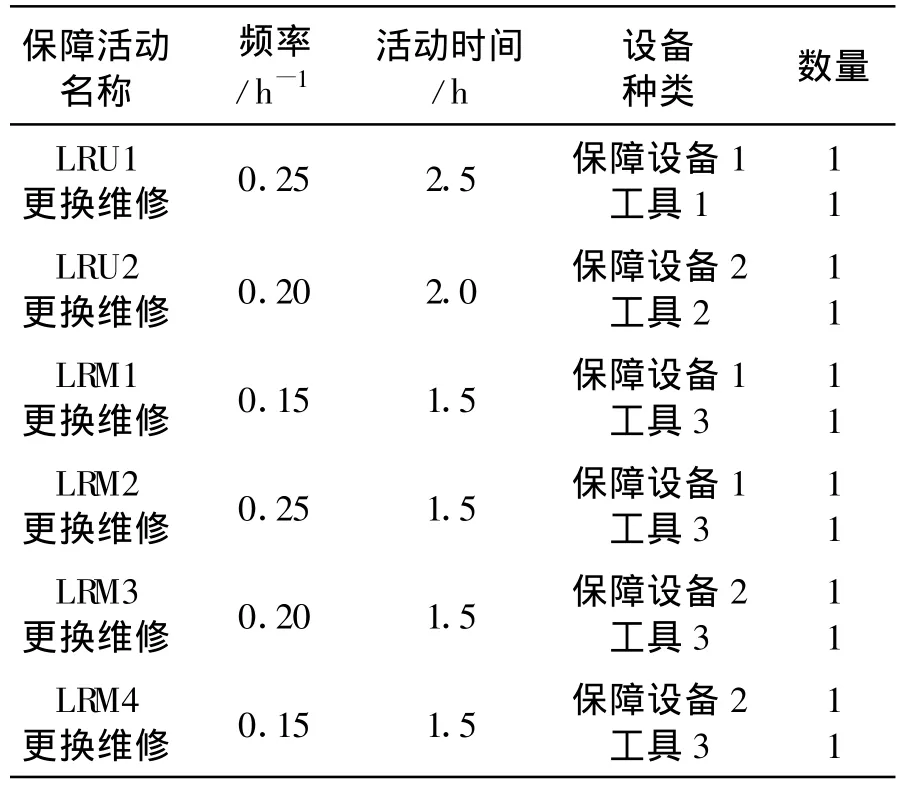
表1 保障活动的保障设备需求数据表Table 1 Support activity′s need for support equipment

由文献[15]中保障资源数量预测方法可得到保障设备数量配置方案为(4,3,2,2,4),可算得在此方案下,外场平均保障满足率为0.6944,保障设备利用率的均值为0.2263,方差为0.0262。

取保障设备利用率均值与方差的约束值为 ρ0=0.2263,D0=0.01,建立以保障设备利用率的均值和方差为约束条件,以平均保障设备满足率为目标的优化模型。采用AGA算法求解得到优化的保障设备配置方案为(5,4,3,2,4),该方案对应的外场平均保障设备满足率为0.9528,保障设备利用率均值为0.2388,方差为0.0007。优化过程曲线如图2所示。

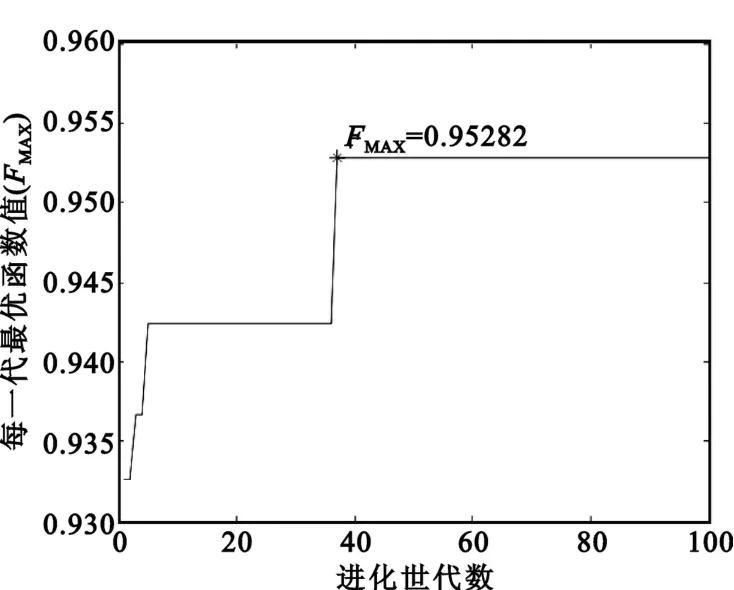
图2 AGA优化过程曲线Fig.1 AGA optimizing process curve

与原方案进行对比分析可知,优化后的方案显著提高了外场保障设备满足率,降低了保障设备利用率的方差,使各保障设备得到了更加合理充分的利用,提高了保障设备的配置效率。

6 结 论

本文建立的保障设备配置优化模型在保障设备满足率的计算过程中考虑了保障活动与保障设备之间4种不同的关系(1∶1、1∶N 、N∶1和 N∶M),更加符合工程实际情况;模型在优化目标与约束条件设定时考虑了保障系统的及时性、部署性和经济性要求,能够对保障站点内多类保障设备的配置数量进行联合优化,在整体上提高了保障设备的配置效率,为研制部门解决保障设备配置数量不合理的问题提供科学有效的方法。

[1]吴正勇.飞机设计手册(第21分册):产品综合保障[M].北京:航空工业出版社,2000.WU Zheng-yong.Aircraft design manual(21th fascicule):product integrated support[M].Beijing:Aviation Industry Press,2000.(in Chinese)

[2]郭红芬,刘福胜.利用排队模型优化保障设备数量[J].装甲兵工程学院学报,2005,19(1):29-31.GUO Hong-fen,LIU Fu-sheng.Use queue theory mode tooptimize the quantity of the support equipment[J].Journal of Academy of Armored Force Engineering,2005,19(1):23-31.(in Chinese)

[3]曲丽丽.装备研制阶段保障系统评价方法研究[D].北京:北京航空航天大学,2009.QU Li-li.Research of Support System Evaluation in the Materiel Development Phase[D].Beijing:Beihang University,2009.(in Chinese)

[4]刘瑞,康锐,张侦英.装备研制阶段保障设备配置效率预测模型[J].系统工程与电子技术,2011,33(5):1040-1044.LIU Rui,KANG Rui,ZHANG Zhen-ying.Prediction model for allocation efficiency of support equipment in products developing phase[J].Systems Engineering and Electronics,2011,33(5):1040-1044.(in Chinese)

[5]张侦英.装备研制阶段保障资源配置效率分析方法研究[D].北京:北京航空航天大学,2010.ZHANG Zhen-ying.The analysismethod on the allocation efficiency of logistics resources in equipment designing process[D].Beijing:Beihang University,2010.(in Chinese)

[6]王乃超,康锐,王宇.基于产品维修策略的保障设备需求量计算模型研究[J].系统工程与电子技术,2009,31(5):1266-1269.WANG Nai-chao,KANG Rui,WANG Yu.Research on support equipment number determination model basing on item repair policy[J].Systems Engineering and Electronics,2009,31(5):1266-1269.(in Chinese)

[7]Alfredsson P.Optimization of multi-echelon repairable item inventory systems with simultaneous location of repair facilities[J].European Journal of Operational Research,1997,99(3):584-595.

[8]郭彩芬,王宁生.基于排队理论优选工作站设备数量[J].工业技术经济,2004,23(3):101-102.GUO Cai-fen,WANG Ning-sheng.Optimize the quantity of the support equipment ofworkstationbased on the queue theory[J].Industrial Technology Economics,2004,23(3):101-102.(in Chinese)

[9]Green L,Kolesar P.The Point wise Stationary Approximation for Queueswith Non-stationary Arrivals[J].Management Science,1991,37(1):84-97.

[10]Rolfe A J.A Note on Marginal Allocation in Multiple-Server Service Systems[J].Management Science,1971,17(9):656-658.

[11]GJB451A-2005,可靠性维修性保障性术语集[S].GJB451A-2005,Reliability,Maintenance&Support Terms[S].(in Chinese)

[12]张侦英,康锐.典型情况下保障设备满足计算模型[J].计算机集成制造系统,2010,16(10):2206-2210.ZHANG Zhen-ying,KANG Rui.Support equipment fill rate calculation model under a typical case[J].Computer Integrated Manufacturing Systems,2010,16(10):2206-2210.(in Chinese)

[13]SrinivasM,Patnailk L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Transactions on Systems,Man and Cybernetics,1994,24(4):656-667.

[14]文佳.装备研制阶段保障设备配置优化方法研究[D].北京:北京航空航天大学,2011.WEN Jia.Optimization Method for Support Equipments in theMateriel′s Development Phase[D].Beijing:Beihang U-niversity,2011.(in Chinese)

[15]郭霖瀚,康锐,文佳.以保障活动为中心的装备保障资源数量预测[J].航空学报,2009,30(5):919-924.GUO Lin-han,KANG Rui,WEN Jia.Quantitative forecast of support activity centered equipment support resources[J].Acta Aeronautica Et Astronautica Sinica,2009,30(5):919-924.(in Chinese)