商空间理论在道路交通事故中的应用①

刘国璧， 孙 群， 袁宏俊

(1.安徽电子信息职业技术学院，安徽 蚌埠 233030;2.安徽大学数学与计算科学学院，安徽 合肥 230039;3.安徽财经大学，安徽 蚌埠 233030)

0 引言

“交通事故 (Traffic Accident)”是指车辆在道路上因过错或者意外造成人身伤亡或者财产损失的事件.道路交通事故预测是指通过对过去已发生的交通事故的数据状态进行分析研究，对将来可能发生的交通事故做出推断和预测，理清道路交通事故发生的规律和发展趋势，对提高道路交通安全管理水平有一定的促进作用[1].对于道路交通事故的预测，有很多学者已经进行了研究[2～5]，采用的预测方法主要有:灰色理论法、回归法、LS－SVM法、马尔可夫法、多层递阶法、神经网络法以及组合法[6～7]等，但由于交通事故的复杂性和随机性，许多预测效果不理想，难以得到满意的结果.

小波神经网络是小波理论和神经网络的结合，它在很多领域得到了广泛的应用，目前在道路交通事故的预测研究中，还没有利用小波神经网络与商空间结合进行的研究.本文提出基于商空间的小波神经网络模型，利用商空间理论找出大小合适的粒度，用小波神经网络对对道路交通事故的结果进行预测，并对预测效果进行评价，结果表明文中提出的方法，预测的精度较高，预测的效果较好.

1 基于商空间小波神经网络的道路交通事故研究

1.1 商空间理论

商空间理论是由张钹院士和张铃教授提出的[8]，它将粒度世界与商集概念结合起来，在研究实际问题时，从不同的角度或范围来分析它，用不同的粒度对所研究的问题进行描述，在不同的粒度空间上对问题进行研究.商空间理论在很多文献中均有叙述，在此不再雷述.

用三元组(X，f，T)描述道路交通事故问题时，从酒驾、车速、猛拐、气温、天气情况和违反交通标志线共6个属性来考察道路交通事故情况，即f=(f1，f2，f3，f4，f5，f6).可以利用一些时间属性函数(例如10天的时间属性)对论域进行划分，得到新的粒度空间([X]，[f]，[T]).

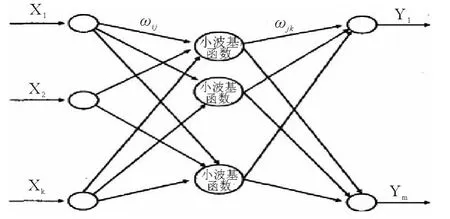
图1 小波神经网络的拓扑结构

1.2 小波神经网络

小波神经网络(Wavelet Neural Networks，WNN)是一种以BP神经网络拓扑结构为基础的新兴的数学建模方法，以小波基函数作为隐含层节点的传递函数，信号前向传播的同时误差反向传播，其拓扑结构如图1所示.

其中，输入层为 X1，X2，…，Xk，输出层为 Y1，Y2，…，Ym，神经网络的权值为 ωij，ωjk.

隐层计算公式为:

(1)式中，h(j)是小波基函数，hj的平移因子是bj.

Morlet母小波基函数为:

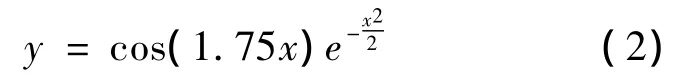
输出层计算公式为:

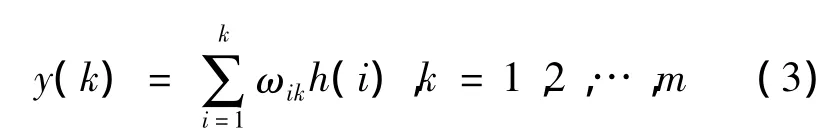
利用梯度修正法对WNN的权值和小波基函数进行修正[9]，预测误差公式为:

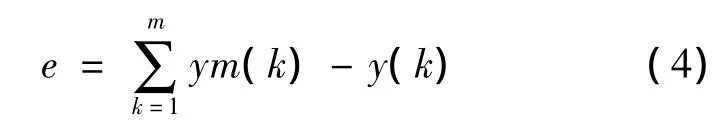
根据误差e对WNN的权值和小波基系数进行修正.

1.3 模型描述

利用商空间的属性函数划分法对粒度进行选取，并将之作为WNN的输入样本，通过多次试验，找出“最优”粒度，然后在该粒度空间中分析解决问题.所采用的方法模型如图2所示[10].

图2 商空间小波神经网络的道路交通事故预测模型

2 道路交通事故预测实验

2.1 模型数据介绍

文中数据源于某市交警队事故处理大队，计算过程利用Matlab软件进行仿真模拟.数据选取了2009年9月1日至2012年9月1日共3年的交通事故影响因子和交通事故次数进行分析，影响因子为:酒驾、车速、猛拐、气温、天气情况和违反交通标志线，这6个影响因子和交通事故次数共7个属性值构成一个样本.文中采用的WNN分为输入层、隐层和输出层，输入层有6个节点，为6个交通事故属性值，输出层有1个节点，为预测的交通事故次数值.采用属性函数划分法对原始数据取均值，得到下面6种大小不同的粒度划分[11]:

粒度1:由原始数据构成.2009年9月1日至2010年8月31日样本365个，2010年9月1日至2011年8月31日样本365个.

粒度2:用3天时间属性划分原始数据，2009年9月1日至2010年8月31日样本120个，2010年9月1日至2011年8月31日样本120个.

粒度3:用5天时间属性划分原始数据，2009年9月1日至2010年8月31日样本72个，2010年9月1日至2011年8月31日样本72个.

粒度4:用8天时间属性划分原始数据，2009年9月1日至2010年8月31日样本44个，2010年9月1日至2011年8月31日样本44个.

粒度5:用12天时间属性划分原始数据，2009年9月1日至2010年8月31日样本29个，2010年9月1日至2011年8月31日样本29个.

粒度6:用15天时间属性划分原始数据，2009年9月1日至2010年8月31日样本23个，2010年9月1日至2011年8月31日样本23个.

2.2 实验结果

实验1用2009年9月1日至2010年8月31日的120个数据作为学习样本，2010年9月1日至2011年8月31日的120个数据作为测试样本，仿真结果如表1所示.

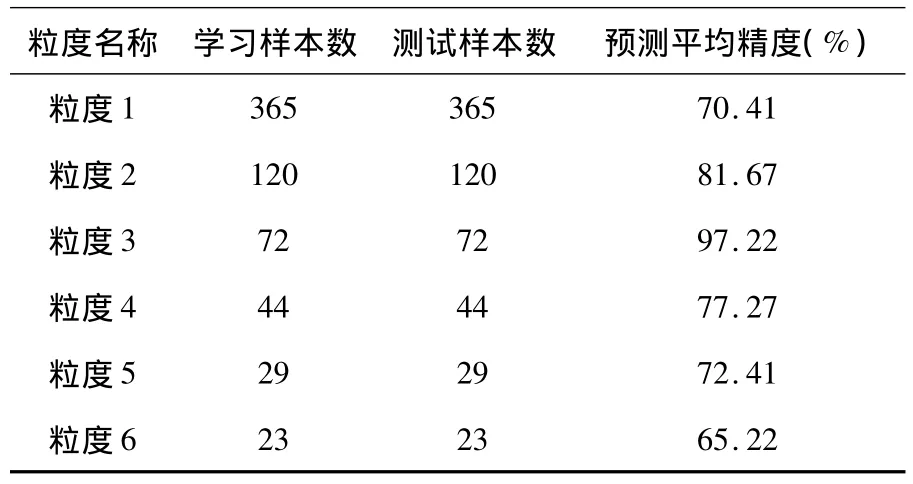
表1 实验1仿真结果表

实验22009年9月1日开始的60个样本作为学习样本，2011年9月1日开始的60个样本作为测试样本.

实验32010年9月1日至2011年8月31日一年的数据作为学习样本，2011年9月1日至2012年8月31日的数据作为测试样本.

实验42009年9月1日至2011年8月31日两年的数据作为学习样本，2011年9月1日至2012年8月31日的数据作为测试样本.

实验2～4的结果如表2和图3－5所示.

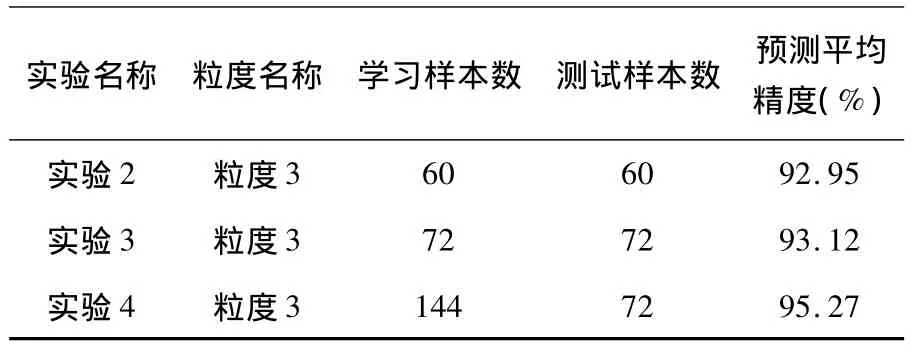
表2 粒度3实验结果表

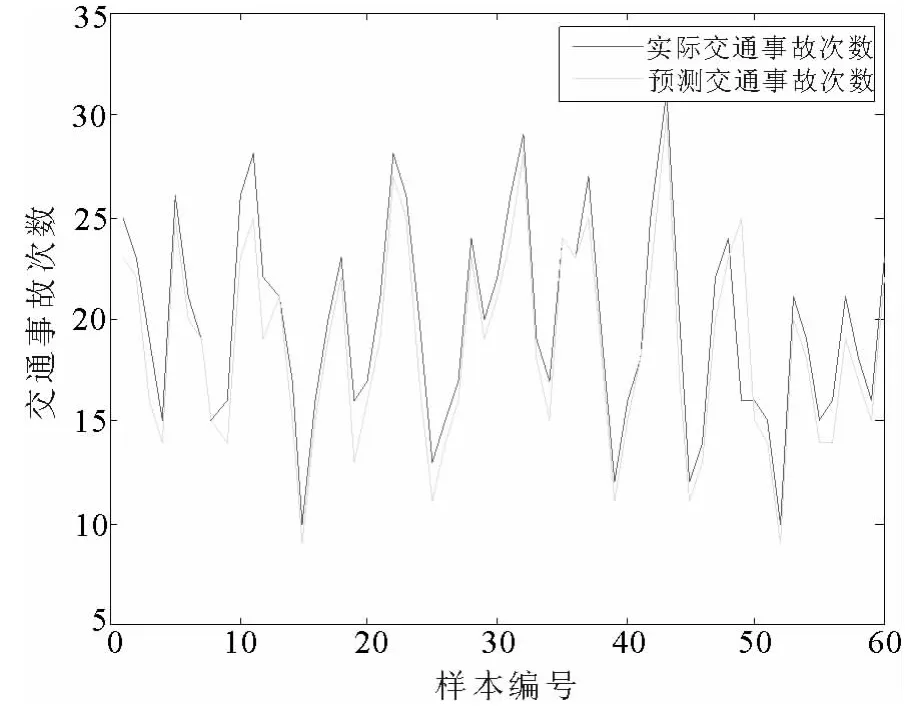
图3 粒度3实验2预测结果图

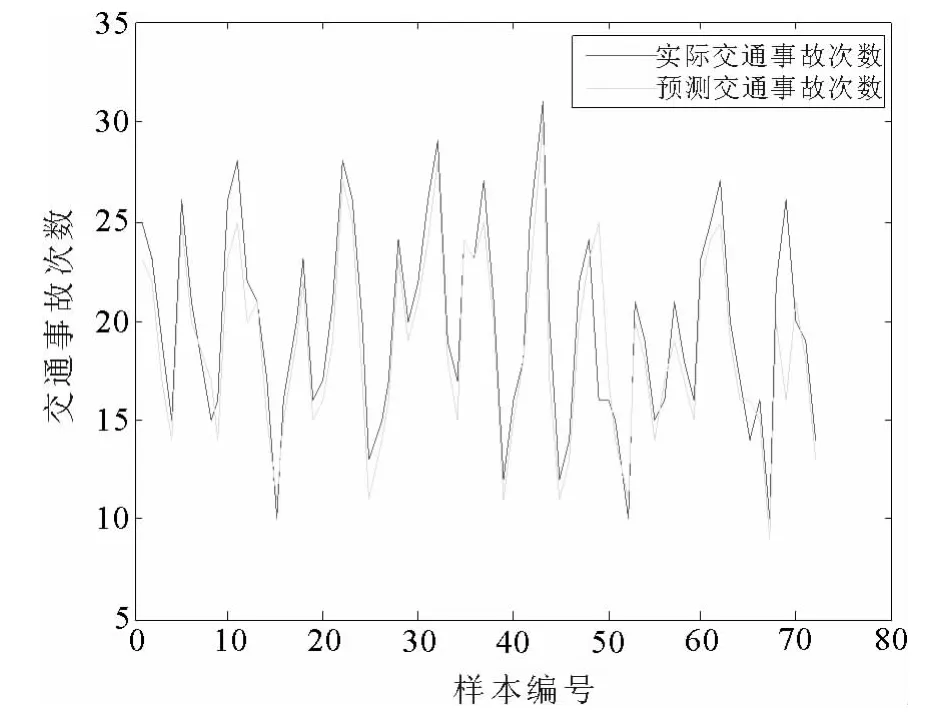
图4 粒度3实验3预测结果图

2.3 结果分析

实验1用2009年9月1日至2010年8月31日的120个数据作为学习样本，2010年9月1日至2011年8月31日的120个数据作为测试样本，选取了6种不同大小的粒度，表1是实验1预测的精确度对比，由表1可知，预测的准确度与粒度大小的选取有一定关系，6种粒度中，仿真精度最高的是粒度3，预测精度为97.22%，所以选取粒度3作为问题求解的最优粒度.

为了检验粒度3下的预测效果，进而进行了实验2～4，实验2～4均是在最优粒度3下进行的.其中，实验2是对2011年的60个交通事故样本数据进行预测的，学习样本数据是2009年的60个数据.实验3～4是对2011年9月1日至2012年8月31日的交通事故数据进行预测的，它们采用的学习样本不同.

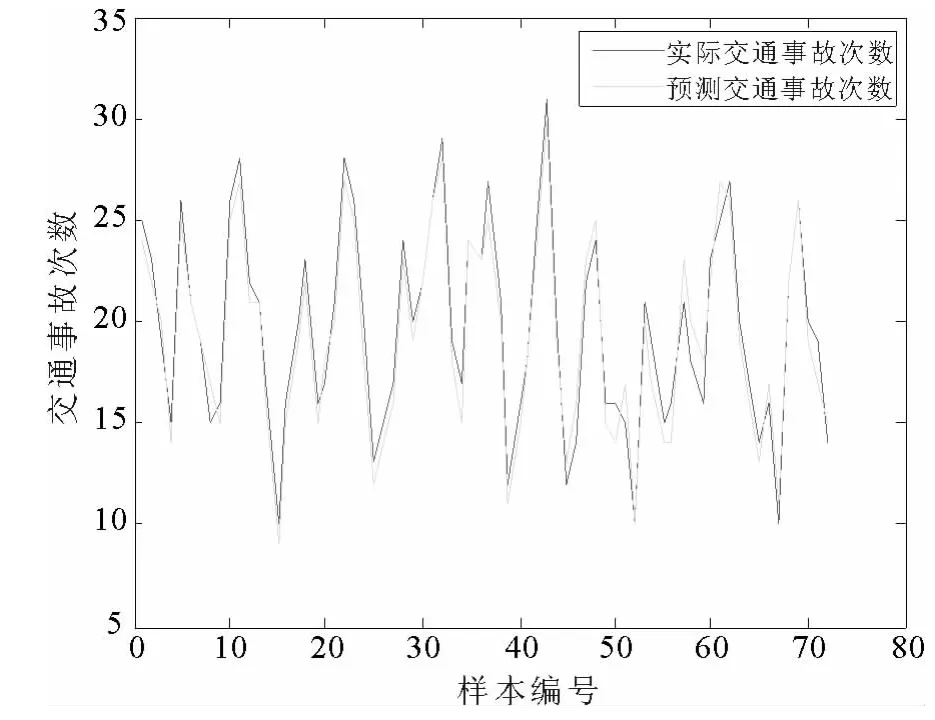
图5 粒度3实验4预测结果图

表2是实验2～4的仿真结果精度对比表，图3～5是仿真实验预测结果图.从表2和图3～5可知，在最优粒度3下进行的实验2～4的预测精度分别是 92.95%，93.12%，95.27%，仿真的精度明显得到了提高.实验结果表明，在最优粒度3下，对2011年9月1日至2012年8月31日的交通事故数据进行预测能取得更好预测效果.

因此，选择大小合适的粒度，对问题求解具有一定的作用，本文通过不断尝试，选出最优粒度，更好地解决了问题，仿真精度更高、效果更好.

3 结束语

本文提出了商空间理论和小波神经网络的道路交通事故预测方法，利用商空间理论，将所研究问题的论域粒度化，把原研究问题转化到新的问题求解空间中，找出本问题的最合适的粒度，将之作为WNN的输入，提高了预测的精度，取得了较好的结果，达到了建模的目的.

[1]孟杰.道路交通事故灰色预测模型的建构与应用研究[J].华东交通大学学报，2006，23(5):55 －57.

[2]乔向明.中国道路交通事故变化趋势预测[J].长安大学学报:自然科学版，2004，24(6):64－66.

[3]周维新.交通事故灰色预测模型的研究[J].西安公路交通大学学报，2000，20(2):73－75.

[4]李相勇.道路交通事故灰色马尔可夫预测模型[J].公路交通科技，2003，20(4):98－101.

[5]王福建.道路交通事故灰色Verhulst预测模型[J].交通运输工程学报，2006，6(1):122－126.

[6]衰伟，等.道路交通事故死亡人数预测模型[J].交通运输工程学报，2007，7(4):112－116.

[7]钟波，汪青松.基于组合预测理论的交通事预测研究[J].交通科技与经济，2006，5:107－108.

[8]张玲，张钹.商空间理论与粒度计算[J].计算机科学，2003，30(5):26—29.

[9]MATLAB中文论坛.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社，2010.

[10]汪小寒.基于动态粒度小波神经网络的空气质量预测[J].计算机工程与应用，2013，6:221－224.

[11]张月琴.商空间理论在道路交通事故分析中的应用[J].电脑开发与应用，2011，3:22－25.