浮置板轨道对地铁车辆振动影响的实测分析

李再帏 练松良 刘晓舟

（1.上海工程技术大学城市轨道交通学院，201620，上海；2.同济大学道路与交通工程教育部重点实验室，201804，上海／／第一作者，讲师）

近年来，城市轨道交通在我国得到迅速发展，给人们的生活带来了极大的便利，但随之而来的噪声与振动问题也引起社会的广泛关注。浮置板轨道作为现有各类减振型轨道结构中减振性能最优的轨道结构［1］，在城市轨道交通中得到广泛使用。目前，国内外学者对浮置板轨道结构的研究多集中在其减振性能上［2－4］，但对敷设浮置板轨道后列车运行的平稳性和舒适性研究较少；而现有的列车运行平稳性测试则集中于整体道床上［5－8］。因此，本文采用现场测试的方法，对浮置板轨道结构的线路进行测试，并与普通整体道床轨道结构进行比较，分析和研究浮置板轨道对地铁车辆振动的影响。

1 车辆振动试验及数据处理

1.1 线路状况

某地铁线路敷设的浮置板地段下穿一三甲医院，线路线型为直线；线路上运行的车辆为6节编组的A型地铁列车；线路的上、下行方向均铺设浮置板轨道，长度各为120m，分别包括4块30m长的浮置板。整个浮置板轨道结构已经使用6年，钢轨状态、车辆运行及保护对象均未发生异常。

由于该地段的轨道高度仅为570mm，因轨下空间所限，所以采用承轨槽式浮置板的设计。通过在两侧及中部加设凸台，提高板的刚度、强度及参振质量。由于板的厚度较薄，所以该段浮置板轨道的隔振效果仅相当于目前轻量级的浮置板轨道，其理论频率为8.6Hz，理论计算减振效果为17.6dB。

1.2 测点布置与试验工况

按照规范［10］中关于车体加速度测点布置的规定，车辆测点布置位置应当位于车辆转向架心盘上方的车厢地板上。对于A型车而言，测点布置如图1所示。

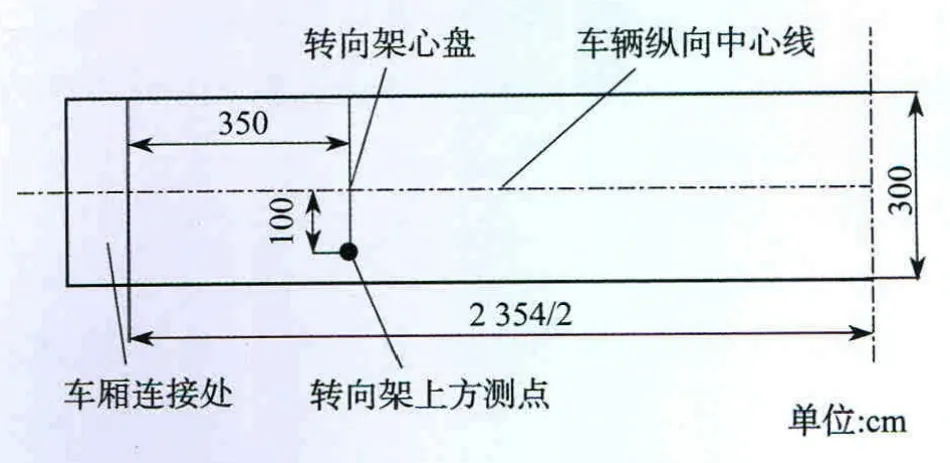
图1 轨道车辆内部振动加速度测点布置图

测试设备由图2中的891型传感器和891型六线放大器等组成，并利用自制的实时监测设备进行信号采集，采样频率设为500Hz。测试工况为满载状态的地铁列车通过线路20次。

图2 测试仪器实景图

1.3 数据处理

1.3.1 振动加速度

车辆的加速度值分析采用幅值和有效值两种方法。其中，幅值的选取主要在竖向或横向时域信号中读取绝对值的最大值，再对其取半峰值即可，并与《铁路线路维修规则》［11］进行比较；而有效值则利用式（1）进行计算，用以评价车辆振动能量的大小，并兼顾了振动时间历程的全过程。

式中：

xrms——在T时间段内的车辆振动加速度有效值；

x（t）——在时刻t的车辆振动加速度有效值。

1.3.2 平稳性指标

车辆的平稳性是评定乘客对振动环境舒适感觉的主要依据。我国地铁车辆平稳性的标准主要采用Sperling公式来计算平稳性指标。Sperling平稳性指标W 可按式（2）计算。

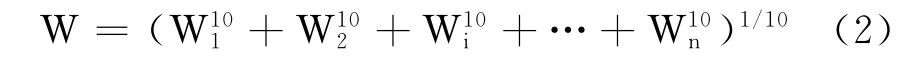
式中：

Wi——每一种频率成分所对应的平稳性指标值。

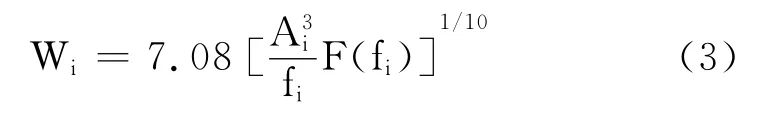
式中：

Ai——振动波形进行频谱分析后频率fi所对应的加速度幅值，单位以重力加速度g计；

F（fi）——频率fi所对应的频率修正系数。

客车的Sperling平稳性指标的评定等级分为三级，如表1所示。

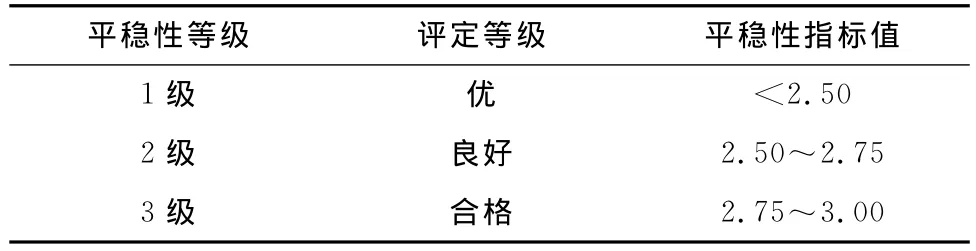
表1 客车的Sperling平稳性指标的评定等级

1.3.3 功率谱分析

车辆加速度功率谱可反映列车在不同轨道结构上运行时车辆振动的剧烈程度，同时还可分析其主要的振动频率。

对于一个车辆振动加速度函数X（t），在时间范围［－m，m］取其一段函数 Xm（t），则过程Xm（t）的样本函数xm（t）满足有限能量条件。通过傅里叶变换可得单边功率谱密度Gx（f）［7］：

式中：

f——样本频率；

Sx（f）——双边功率谱。

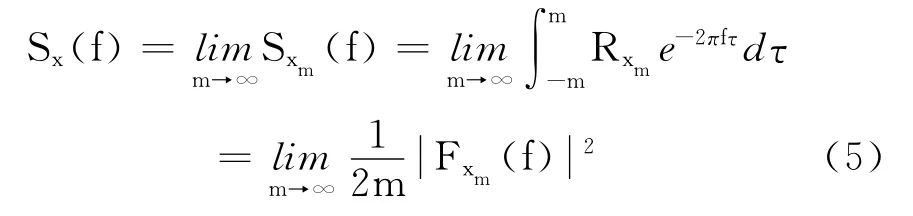
式中：

Fxm（f）——样本函数xm（t）的傅里叶变换；

Sxm（f）——样本长度为2m的估计功率谱；

Rxm——样本长度为2m的相关函数。

2 试验结果与分析

2.1 幅值及有效值分析

对测取的20组车辆振动加速度数据进行分析。每组数据的加速度幅值和有效值按上述方法进行计算，分别得到其平均值和最大值。计算结果如图3所示。

从图3中可知：

1）车辆在浮置板轨道上竖向、横向振动加速度幅值平均值比在普通整体道床轨道大。对于车体竖向振动加速度幅值的最大值而言，浮置板轨道比普通整体道床轨道大；对于车体横向振动加速度幅值的最大值而言，浮置板轨道比普通整体道床轨道略小。

2）车体竖向、横向加速度有效值的平均值和最大值，浮置板轨道均比普通整体道床轨道大。

3）车体竖向、横向加速度幅值均小于《铁路线路修理规则》I级标准（横向限值0.06 g，竖向限值0.1 g）。

2.2 平稳性指标分析

利用式（2）和式（3）分别计算20组工况的Sperling平稳性指标，即计算各个平稳性指标的均值和最大值。计算结果如图4所示。

图4 Sperling平稳性指标对比

从图4可知：

1）车辆在通过浮置板轨道时Sperling平稳性指标值均比通过普通整体道床轨道时的大，竖横向的平均值分别大0.12和0.04，竖横向的最大值分别大0.13和0.15。

2）车辆经过两种轨道结构时的竖横向平稳性指标均低于优秀级的限值2.5。

2.3 车辆振动功率谱分析

利用式（4）和式（5）对列车振动加速度进行功率谱计算可知，各组工况的频率结构差别很小，因此这里选取了某一组测试的功率谱密度计算结果进行分析，如图5所示。

由图（5）可知，对浮置板轨道而言，车辆通过时竖向振动加速度主频为1.35Hz；横向振动加速度的主频为1.63Hz，且在5.75Hz和24.85Hz处也有较大的峰值。对普通整体道床轨道而言，车辆通过时竖向振动加速度主频为1.50Hz；横向振动加速度的主频为1.52Hz，且在6.13Hz和24.63Hz处也有较大的峰值。

对比两者的功率谱密度图可知，列车在通过浮置板轨道结构时，车辆的竖向振动频率变化较小，但能量谱幅值较普通整体道床轨道大，说明浮置板对车辆的竖向振动影响较大。而车辆的横向振动无论是在幅值和频率上，浮置板轨道地段与普通整体道床轨道地段差别较小，说明浮置板对车辆的横向振动影响较小。

3 结语

通过对地铁车辆通过浮置板轨道时产生的车辆振动加速度进行测试，并与普通整体道床轨道进行比较分析，可以得到如下结论：

1）车辆通过浮置板轨道时产生的车辆竖向振动加速度的幅值和有效值较通过普通整体道床轨道时的大，横向振动加速度有效值较普通整体道床轨道时的大；但车辆经过两种轨道结构时测试值均小于《铁路线路修理规则》中的I级标准。

2）车辆在通过浮置板轨道时Sperling平稳性指标值均比通过普通整体道床轨道时的大。车辆经过两种轨道结构时车辆竖、横向平稳性指标均低于优秀级的限值2.5。

3）浮置板轨道结构对车辆的竖、横向振动频率影响较小。

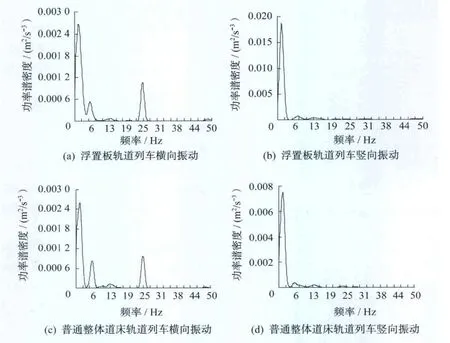
图5 功率谱密度计算结果对比图

4）本文只给出了直线段浮置板轨道对地铁车辆振动的影响，而曲线段浮置板轨道对车辆振动的影响有待作进一步研究。

［1］练松良.轨道工程［M］.北京：人民交通出版社，2009.

［2］王澜，宣言，万家，等.浮置板轨道结构隔振效果仿真研究［J］.中国铁道科学，2005，26（6）：48.

［3］吴川，刘学文，黄醒春.短型浮置板轨道系统隔振性能研究［J］.振动与冲击，2008，27（8）：74.

［4］李增光，吴天行.浮置板轨道二维建模及隔振性能分析［J］.铁道学报，2011，33（8）：93.

［5］朱金龙.高架轨道交通车辆运行舒适度测试与分析［J］.城市轨道交通研究，2003（2）：46.

［6］朱剑月，朱良光，周劲松，等.地铁车辆运行舒适度与平稳性评价［J］.城市轨道交通研究，2007（6）：28.

［7］刘李莹，周文祥，徐娜.铁路车辆运行平稳性指标的测试精度分析［J］.电力机车与城轨车辆，2008，31（1）：38.

［8］黄守域，曹广忠，张华超，等.地铁车辆客室振动测试研究［J］.城市轨道交通研究，2011（4）：99.

［9］GB 5599—85铁道车辆动力学性能评定和试验鉴定规范［S］.

［10］铁运［2006］146号部令.铁路线路修理规则［S］.北京：中国铁道出版社，2006.

［11］耿传智，宫寅.浮置板轨道系统动力响应分析［J］.城市轨道交通研究，2012（3）：14.