MIMO中继系统中预编码的级联算法

郭必忠，居美艳

（河海大学 江苏 南京 211100）

近年来，MIMO系统由于其可以有效的提高频谱效率和网络的覆盖[1-2]的特点，而受到广泛的关注。两跳中继系统是一种简单的中继网络，中继可以采用的传输协议分为:放大重传（AF），译码重传（DF），选择中继（SR），和增量中继（IR）等协议。放大重传协议（AF）是一种最简单的协作模式，是指中继在信号的接收和转发的过程中，不对信号进行调制解调，而是直接把接收到的信号进行模拟放大后转发给目的节点[3-4]，现今关于中继技术研究大多以AF中继为主。

在文献[5-6]中给出了一种在源节点和中继节点以及目的节点的迭代联合算法的设计，但是具有很高的算法复杂度，为了简化算法的复杂的，在文献[7]中给出了一种在中继节点的预编码和均衡技术联合的优化算法。本文提出了级联算法，把中继的两跳过程分解开，相当于把MIMO中继系统分解成两个独立的无中继系统，然后分别单独进行预编码的设计。

1 系统模型

文中研究的系统是一个单用户单中继的MIMO通信系统，系统框架如图1所示。在系统中，只考虑两跳中继网络，而不考虑源节点到目的节点的直接链路。中继在通信过程中采用是时分半双工工作方式，即分为两个时隙：第一时隙，信号从源节点发送到中继节点；第二时隙，信号从中继节点发送到目的节点。中继节点在通信过程中不能同时接收和发送信号。

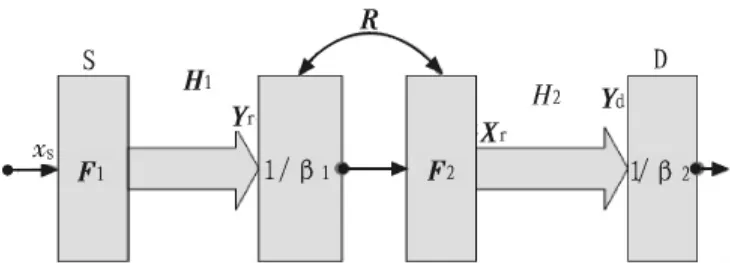
图1 系统模型Fig.1 System model

假设系统发送端天线数为N，中继节点天线数为Q，用户端天线数为M，第一跳从源节点（S）到中继节点（R）之前的信道矩阵为H1，信道噪声为n1，第二跳从中继节点（R）到目的节点（D）之间的信道矩阵为 H2，信道噪声为 n2，输入信号为xs。F1和F2分别为源节点和中继节点的预编码矩阵。将中继节点分成两部分，其中β1表示第一跳中源节点预编码过程的放缩因子。

源节点发射信号经过信道H1到达中继节点，中继节点接收到的信号表示为：

中继节点在接受到信号yr后，乘上后，完成了对H1的预编码过程，得到，再对进行预编码处理后发送到目的节点D，

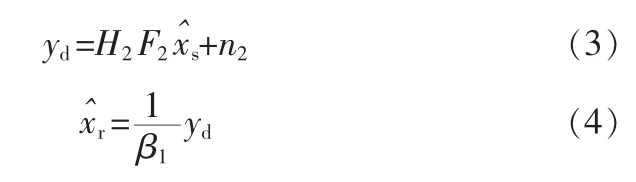
其中β2表示第二跳中的放缩因子，F2表示对第二跳信道矩阵的预编码矩阵H2，为目的节点最终获得的信号。

在构建预编码矩阵F1和F2采用MMSE准则，即在要求与 xs的均方误差最小，与的均方误差最小。

2 两跳级联算法

对于第一跳中，由MMSE准则可以得到下列方程组：

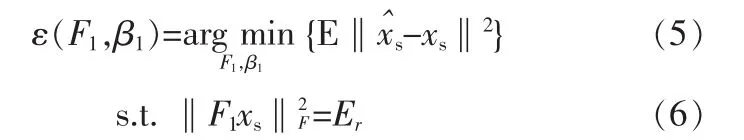
其中，Er表示发送端功率。

由MMSE算法准则[8]可以得到最优的预编码矩阵为

对于第二跳中预编码矩阵F2和放缩因子β2的设计和第一跳相同，于是可以得到

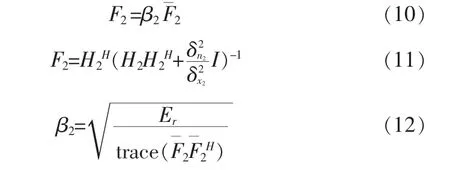
将MIMO中继通信系统分解成两个无中继的点到点系统，并且分别对两跳系统进行预编码处理。信号首先在源节点进行F1处理，到达中继节点进行F2处理，在接收端只要乘以。避免了传统的对源节点和中继节点以及目的节点的联合优化所需要的大量迭代处理。并且为了提高本文算法的性能，在中继节点还可以对信号进行判决，再把判决后的信号在第二跳进行预编码处理。

3 仿真分析

仿真假设天线数N=Q=M=4，SNR1和SNR2分别表示源节点到中继节点以及中继节点到目的节点信噪比，单位（dB），信号采用QPSK调制，仿真数据量为20 000次，图2中比较了在中继节点对进行判决以及不判决的比较。由仿真结果可以看出判决后（dec）的误码率要比未判决（nodec）的低，这是因为在中继节点对判决后，消除了与 xs的部分误差，将那些产生误差但是并未出现误码的信号进行了校正，降低了在第二跳传输中出现误码的概率。

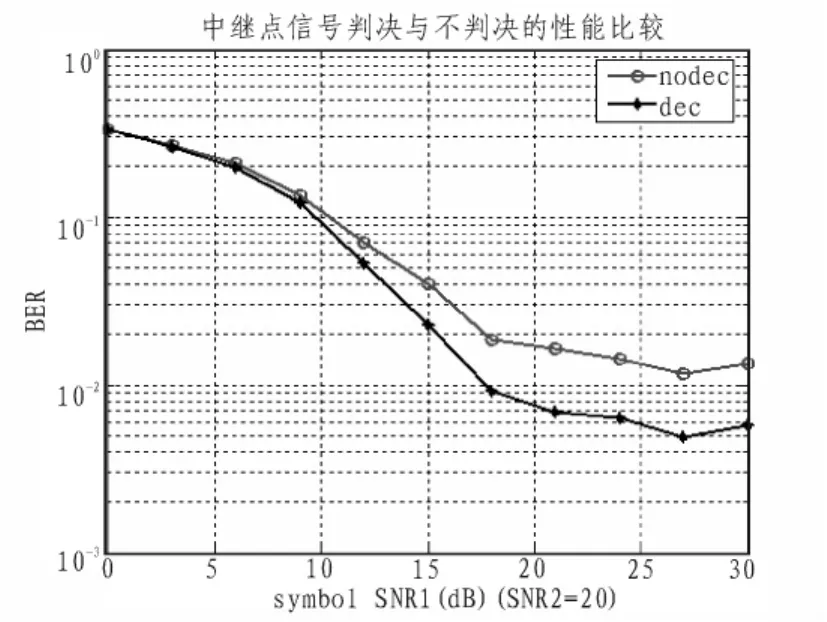
图2 中继点判决比较Fig.2 Signal decision comparison in relay

图3和图4中通过对误码率的仿真，比较了本文方法（tpmmse）和文献[7]中的算法（jmmse），分别是在固定 SNR1=20 dB和SNR2=20 dB的情况下。

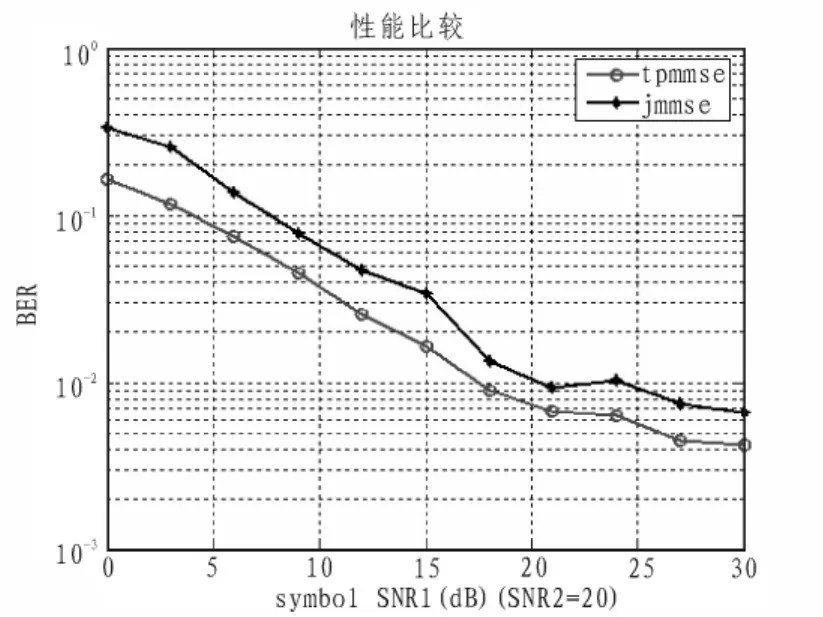
图3 SNR1=20时误码率比较Fig.3 Error rate comparison when SNR1=20

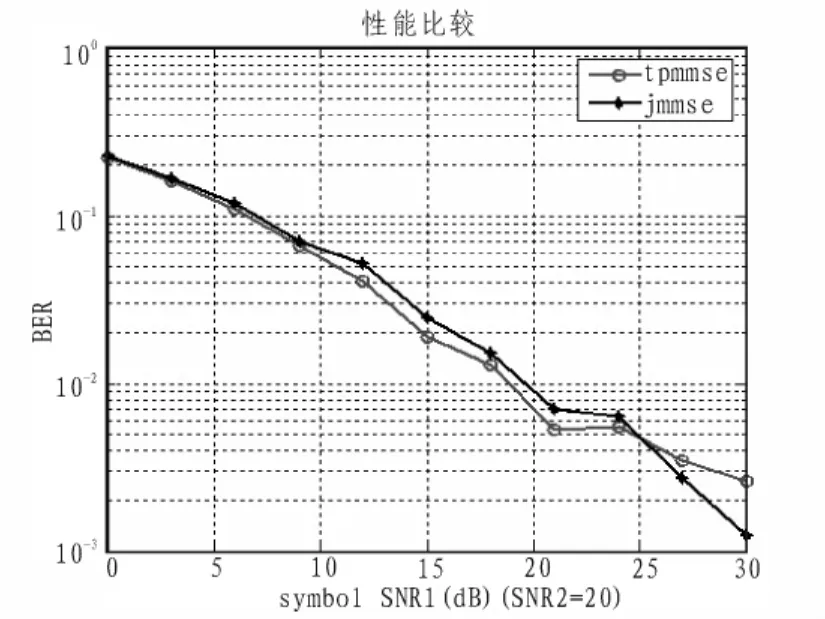
图4 SNR2=20时误码率比较Fig.4 Error rate comparison when SNR2=20

从上述仿真结果比较可以看出，级联算法相比单在中继节点的联合优化算法[7]具有比较好的性能，在图3和图4的共同点SNR1=20，SNR2=20可以看出两个仿真的结果相互印证。在低信噪比的情况下，用文中方法，将要处理的信道干扰分解成俩部分，降低了需要处理的复杂度。在图4可以看出，当两边信噪比都比较高时，信道状态处在比较好的情况时，由于本文方法是分部处理，会有误码率的叠加，性能相较[7]的联合优化反而体现不出提升。

4 结束语

文中给出的在源节点和中继节点的级联预编码可以避免传统的迭代算法的高复杂度，并且通过对误码率的仿真，显示出本文给出的方法在一定程度上优于文献[3]中给出的只在中继节点进行联合优化的算法。在把中继系统分解成两个独立的无中继系统，简化了中继节点设计的复杂度，也便于实现。

[1]Pabst R，Walke B H，Schultz D C，et al.Relay-based deployment concepts for wireless and mobile broadband radio[J].IEEE Commun.Mag.，vol.2004，9（42）:80-89.

[2]Wang B，Zhang J，Madsen A H.On the capacity of MIMO relay channels[J].IEEE Trans.Inform.Theory，2005， 51（1）:29-43.

[3]Tang X J，Hua Y B.Optimal design of non-regenerative MIMO wireless relays[J].IEEE Trans.Wireless Commun.，2007，6（4）:1398-1407.

[4]Medina O M，Vidal J，Agustin A.Linear transceiver design in non-regenerative relays with channel state information[J]IEEE Trans.Signal Processing，2007，55（6）:2593-2604.

[5]Zhang B，Wang X，Niu K，et al.Joint linear transceiver design fornon-regenerative MIMO relay network[J].Electronics Letters，2009，45（24）:24-25.

[6]Mo R H，Chew Y H.MMSE-based joint source and relay precoding design for amplify-and forward MIMO relay network works[J]. IEEE Transactions on Wireless Communications，2009，8（9）:4668-4676.

[7]褚红发，牛凯，贺志强，等.两跳中继通信系统中均衡和预编码联合优化算法[J].北京邮电大学学报，2011，34（8）:5-9.

CHU Hong-fa，NIU Kai，HE Zhi-qiang，et al.An optimal equalization and precoding joint optimization algorithm in dual hop relay systems[J].Journal of Beijing University of Posts and Telecommunications，2011，34（8）:5-9.

[8]Viswanath P Tse D.Sum capacity of the multiple antenna Guassian broadcast channel and uplink-downlink duality[J].IEEE Transactions on Information Theory，2003；49 （8）:1912-1921.