两种被动微波遥感混合像元分解方法比较

顾玲嘉，赵 凯，任瑞治，孙 健，

1.吉林大学电子科学与工程学院，长春 130012

2.中国科学院东北地理与农业生态研究所，长春 130012

0 引言

被动微波遥感技术在全球遥感观测中有着广泛的应用，它能够穿透云层获得地表一定深度的信息[1]。由于星载微波辐射计无法装载大型天线，被动微波数据的空间分辨率都较低[2]。通常使用的星载被动微波辐射计，如SSM／I、AMSR-E和FY3BMWRI的空间分辨率都是几十千米[3-6]。对于观测地区的数据，低空间分辨率导致获得的微波数据是其像元内多类地物的混合结果。

经前期调研[7]，针对星载被动微波数据空间分辨率低导致的混合像元分问题，国内外研究者基于图像处理技术解决的方案主要有2类：一种是图像超分辨率增强方法，另一种是混合像元分解方法。2类方法的实现都可以提高被动微波地物反演参数，但是处理的方法和最终获得的数据有所不同。

被动微波数据超分辨率增强方法可以直接提高亮温的分辨率。其主要的理论依据是卫星的观测数据脚印之间有很多部分的重叠，利用这些重叠观测可以获得更高分辨率的亮温数据，这种方法也是目前国内外研究者多数采用的方法。与之相比，混合像元分解方法对原有被动微波数据处理后，获得的是原混合像元中的各组分亮温，其组分分类根据具体的应用有所不同，组分的获得需要借助于高于被动微波空间分辨率的地物分类数据。将组分亮温数据代入到地物参数反演中，可以提高直接采用混合数据进行反演的结果。例如若直接使用水陆边界处的被动微波混合数据进行海水反演，由于空间分辨率低，该混合像元数据是陆地和海洋的综合结果，相对于海洋表面，陆地表面呈现高发射率，导致反演精度减低。如果通过微波混合像元分解，将该混合像元内的海水组分亮温提取出来并进行海水参数的反演，其反演数据结果的精度肯定是要高于前者。

基于地物分类的被动微波混合像元分解方法取决于微波像元内地物的分类。目前国内外采用的被动微波混合方法主要针对沿海地区水陆分界比较明显的区域进行分解，像元内的地物分类主要分为海洋和陆地，代表方法是Bellerby等[8]结合海岸线数据利用相邻像元信息的混合像元分解方法。Bennartz[9]采用周围完全是陆地类型的亮温数据平均值来代替陆地组分亮温[10-13]，然后代入建立的陆地水体混合像元分解模型，求得天线足印中海洋的组分亮温。MaaB等[14]研究并提出了一种类似于Bennartz的混合像元分解方法，两者的主要差异在于应用领域。MaaB应用该方法来提高海冰参数，而Bennartz利用该方法实现大气参数的反演[15]。在Bellerby提出的微波混合像元分解算法的基础上，笔者[16]曾提出基于水陆分类信息的被动微波混合像元分解方法，并对2010年中国吉林省永吉县洪涝灾害进行了有效评估。

上述被动微波混合像元分解方法都是利用已知地物分类的先验知识，建立被动微波混合像元分解模型，通过求解方程组获得被动微波混合像元中水体和陆地的组分亮温，其有效性的验证都是根据具体的研究地区展开，在各自研究的地区内可以保证其组分亮温求解的精度。其中，Bennartz提出的基于陆地组分亮温的混合像元分解模型相对简单，其陆地组分亮温是由周围完全是陆地类型的亮温数据平均值计算得到；因此，这种模型的适用范围较小。笔者提出基于地物分类信息的被动微波混合像元分解方法，并将其与Bellerby提出的分解方法进行对比研究。考虑到实际测试场地中较难获得不同地物的被动微波组分亮温数据，笔者通过模拟具有不同组分亮温分布的观测地区，设计具有不同组分亮温分布的观测地区，对2种分解方法进行评价，进一步分析2种分解方法的适用范围和影响其求解精度的主要因素，为建立具有更高求解精度和适用范围的被动微波混合像元分解方法提供理论基础。

1 基于地物分类信息的被动微波混合像元分解方法

Bellerby假设相邻9个像元区域中陆地和海洋组分的亮温值相同，这样会使计算结果产生一定误差[16]；笔者在 Bellerby算法[17]的基础上，针对其算法的局限性进行改进。已知被动微波混合像元亮温值TB，混合像元中水体分布比例矩阵PW和陆地分布比例矩阵PL，考虑到邻近区域内水体被动微波组分亮温变化不大的特征，可对m×n窗口尺寸内的被动微波混合数据进行分解，通过构建方程组求解水体组分亮温TW和陆地组分亮温TL：

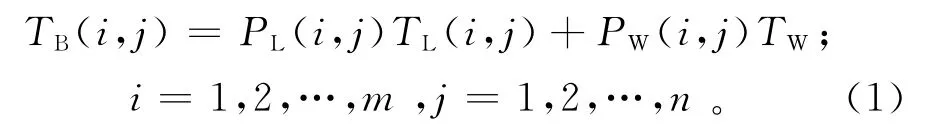
令L（i，j）为水体陆地分类结果。当点（i，j）是陆地上的点时，L（i，j）为1；当点（i，j）是水体的点时，L（i，j）为0。水体陆地分类结果来自于观测地区土地利用分类数据。则P（i，j）为天线增益函数¯G与水体陆地分类结果的卷积：

此外，还需设计一个目标函数作为判断可能解优劣的标准。选取F作为目标函数，ξ为事先给定的阈值，其取值取决于对解的精度要求。目标函数F定义为

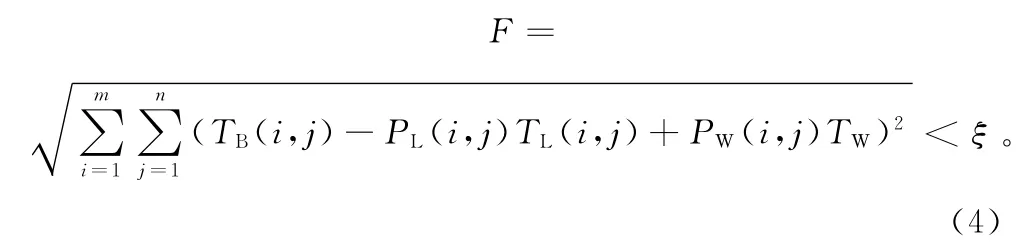
该混合像元分解模型中，m×n方程组中有m×n＋1个未知量，即TL中的m×n个量和TW。这种方程数小于未知量数的方程组属于欠定方程组，有无穷多组解，求得最优解是该算法需要解决的问题。

笔者提出在整个解空间中搜索最优解的计算方法，对不同类型的组分亮温值设定其对应的取值区间。具体采用k-means聚类算法对所有的被动微波亮温数据进行统计分类，聚类后的中心值代表不同组分的综合初值，即CL和CW。根据陆地被动微波混合像元的统计结果如均值、最大值、最小值、方差，以及混合像元中不同组分的比例，计算陆地亮温的变化阈值RL，确定TL（i，j）初值选取范围是[CLRL，CL＋RL]；同理，计算水体亮温的变化阈值RW，确定TW初值选取范围是[CW-RW，CW＋RW]。由于水体亮温应小于陆地亮温，需满足CW＋RW＜CL-RL，对初值选取范围进行重新设定。

根据目标函数调整搜索窗口尺寸m×n，采用带约束条件的非负最小二乘法迭代运算求得最优解。由于初值的选取范围考虑到不同地物的亮温变化空间，且存在多个条件限制方程组的求解范围，因此采用笔者提出的方法可以得到较好的最优解。

2 仿真实验与分析

仿真实验中，首先设计星载被动微波天线增益函数，将其与具有不同模拟组分亮温值分布的观测地区进行卷积，获得该地区的微波混合像元亮温；然后，分别采用Bellerby和笔者提出的分解方法对混合像元进行分解；最后，将其各自分解后得到的组分亮温与原始组分亮温进行比较，进而验证2种被动微波混合像元分解方法的有效性。

2.1 微波天线增益函数

通常，星载微波天线增益函数近似满足二维高斯分布。实际的天线增益方向图是一个包括旁瓣的复杂三维结构，Drusch等[18]研究表明天线函数可以近似为高斯分布函数。因此，天线增益函数的公式定义为

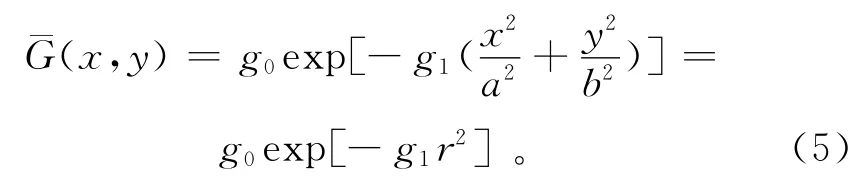
其中：g0和g1是描述高斯分布的常数；x和y是当前位置到测量中心点的水平和垂直距离；a和b表示-3dB椭圆的半轴，可以根据被动微波数据中不同频率对应的足印来确定；椭圆半径r定义为

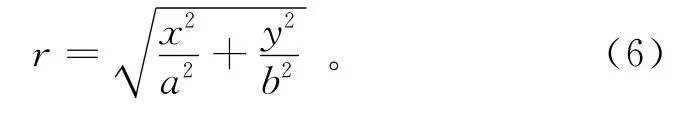
-3dB点定义为从中心点到天线增益降低到最大值一半的位置，Drusch等[18]将式（6）代入式（5），推导得到

本研究使用-3dB点作为椭圆半径，则微波天线增益函数为

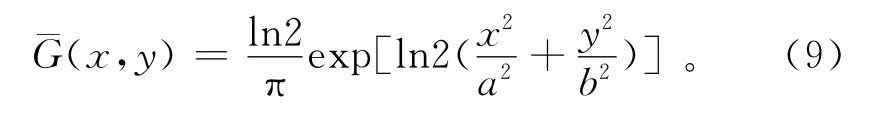
2.2 试验样区设计

假设观测区域为75km×75km的范围，组分亮温网格的空间分辨率为5km×5km，则共包含有15×15个网格。令被动微波数据的采样分辨率为25km×25km，考虑到相对于其他地表类型，水体类型的被动微波遥感数据亮温值变化的动态范围较小，根据被动微波遥感数据AMSR-E和MWRI的主要下垫面辐射亮温统计特性，分别采用如下方案进行样地组分亮温设计。

方案一：假设观测地区内所有陆地组分亮温相同，为260K，所有水体组分亮温相同，为120K。水体组分亮温在区域呈十字分布，令水体比例逐渐增加，构成被动微波组分亮温。具体组分亮温分布比例如图1a、b所示，其中蓝色的图像位置代表水体，红色的图像位置代表陆地，都呈十字分布。由于定义的天线增益函数中椭圆的长短半轴均为25km，所以用每5×5网格的组分亮温与天线增益函数作卷积计算，计算后得到的模拟被动微波混合亮温数据为3像元×3像元，具体值如图1c、d所示。由图1c、d可见，水体组分亮温比例的增加使混合像元亮温数据的十字中心位置更接近水体组分的亮温值，即表现为蓝色图像。

分别采用Bellerby和笔者提出的方法对微波混合像元进行分解，笔者提出的模型采用的窗口尺寸与Bellerby方法一致，为3像元×3像元，其各组分亮温的初值选取由地物分类矩阵中各地物的比例动态估计。将2种模型分解后得到的组分亮温与原始组分亮温进行比较。实验结果表明：在方案一条件下，2种方法求得的组分亮温与原组分亮温的误差为0K，即满足该条件下，2种方法都可以完全获得混合像元的组分亮温。

方案二：假设观测地区内所有陆地组分亮温相同，为260K；所有水体组分亮温相同，为120K。水体组分亮温位置在区域呈随机分布。令水体比例逐渐增加，构成被动微波组分亮温。其具体分布如图2a、b所示。计算后得到的被动微波混合亮温数据如图2c、d所示。从图2c、d可见，水体组分亮温的随机分布使得混合像元亮温数据的分布也较随机，与方案一中混合像元亮温呈十字分布有所不同。

实验结果表明：在方案二条件下，采用Bellerby方法和笔者提出的方法求得的组分亮温与原组分亮温的误差也为0K。

方案一和方案二的结论证明：对于地物类型仅为水体和陆地2类的观测地区，若模型求解区域对应的观测地区中陆地亮温组分相同、水体亮温组分相同，只要已知地物分类信息，无论水体的位置和比例如何变化，采用这2种混合像元分解模型均可以从被动混合像元中准确地获得对应的水体和陆地组分亮温。

方案三：假设当观测地区没有水体时，陆地组分亮温每列相同，且从第1列到第15列由246K到260K递增变化，变化精度为1K（图3a）。当观测地区含有水体时，根据相邻微波亮温数据中水体组分亮温变化不大的特点，仍假设观测区域内水体组分亮温相同，为120K，且水体组分亮温位置与方案二中的分布位置和比例变化相同，即呈随机分布并逐渐增加，构成如图3b、c所示的被动微波组分亮温。将亮温组分数据和天线增益方程进行卷积计算，得到其对应的被动微波混合亮温如图3d、e、f所示。图3d中，由于水体组分亮温的比例为0，因此构成的混合像元亮温图仍是陆地分布。随着水体组分亮温比例增加，其对应的混合像元亮温图3e、f由黄色向蓝色变化，即水体比例的增加使得构成的混合像元亮温数据值降低。

观测地区陆地和水体组分亮温的数据统计结果和采用2种方法计算得到的组分亮温与实际组分亮温差值的统计结果见表1和表2。

由表1和表2可见，当水体比例由0逐渐增加时：对于陆地组分亮温，Bellerby方法得到的组分亮温绝对误差的平均值约为3.1K，而笔者提出方法获得的组分亮温绝对误差的平均值约为0.1K；对于水体组分亮温，Bellerby方法得到的组分亮温绝对误差的平均值约为5.9K，笔者提出方法获得的组分亮温据对误差的平均值约为0.2K。当观测地区陆地组分亮温变化时，由于Bellerby采用的混合像元分解方法假设3×3混合像元内所有陆地组分亮温相同，所有水体组分亮温也相同，因此采用最小二乘法求得的陆地组分亮温精度与3×3混合像元区域即75km×75km范围内的组分亮温变化有关。与之相比，笔者采用的混合像元分解模型假设3×3混合像元中每个混合像元内的陆地组分亮温相同，即每25km×25km范围内的陆地组分亮温一致，同时假设所有混合像元中的水体组分亮温相同，因此采用该方法求得的陆地组分亮温的误差主要来自于25km×25km范围（即5×5个组分亮温网格）内陆地组分亮温的变化。因此，笔者提出的方法能得到更加准确的分解结果。

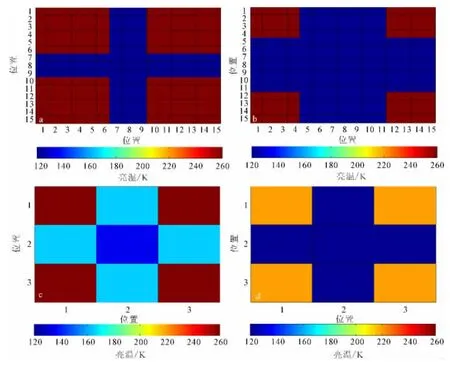
图1 方案一组分亮温分布和混合像元亮温Fig.1 The distribution of component brightness temperature and mixed data in the first project

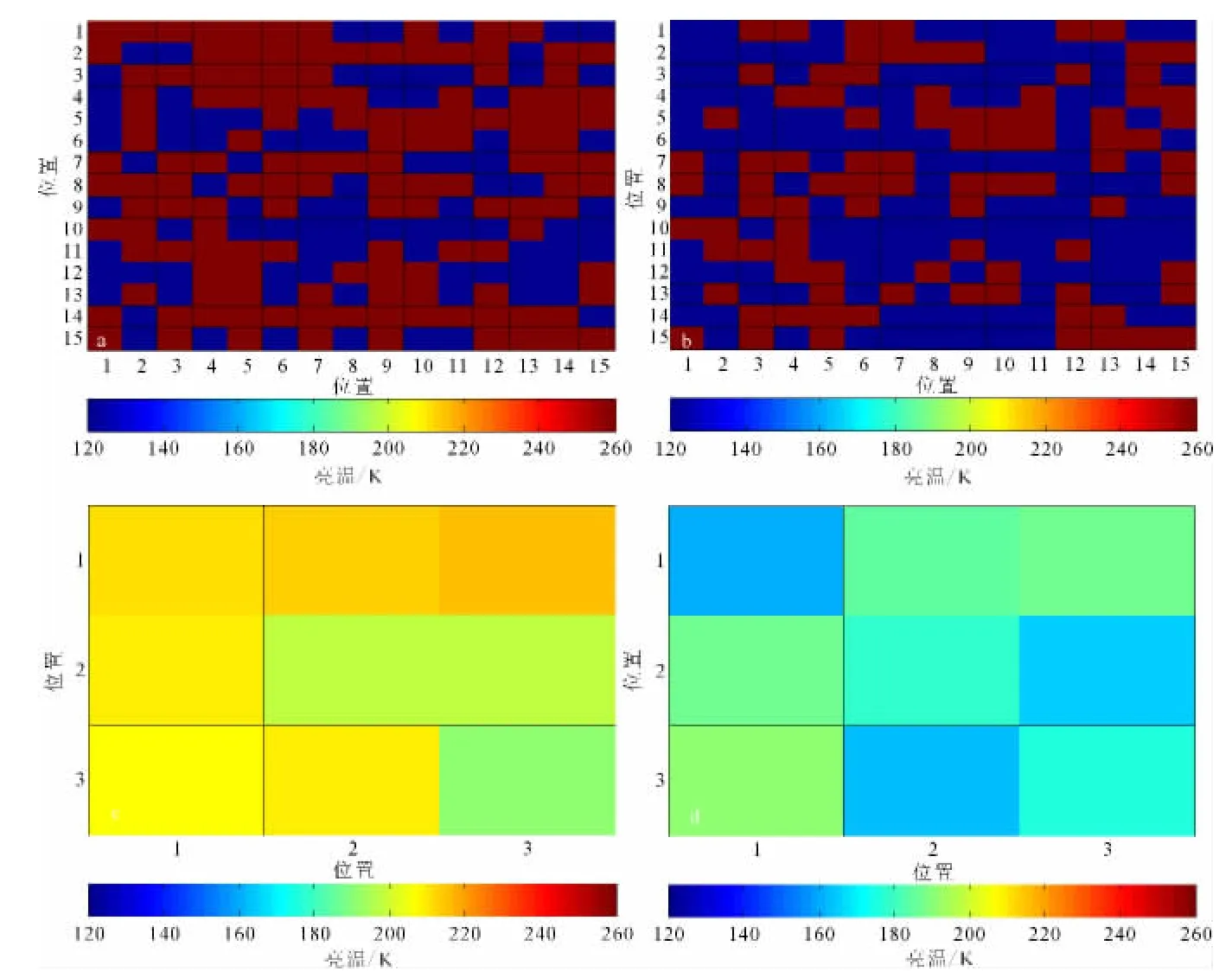
图2 方案二中组分亮温分布和混合像元亮温Fig.2 The distribution of component brightness temperature and mixed data in the second project

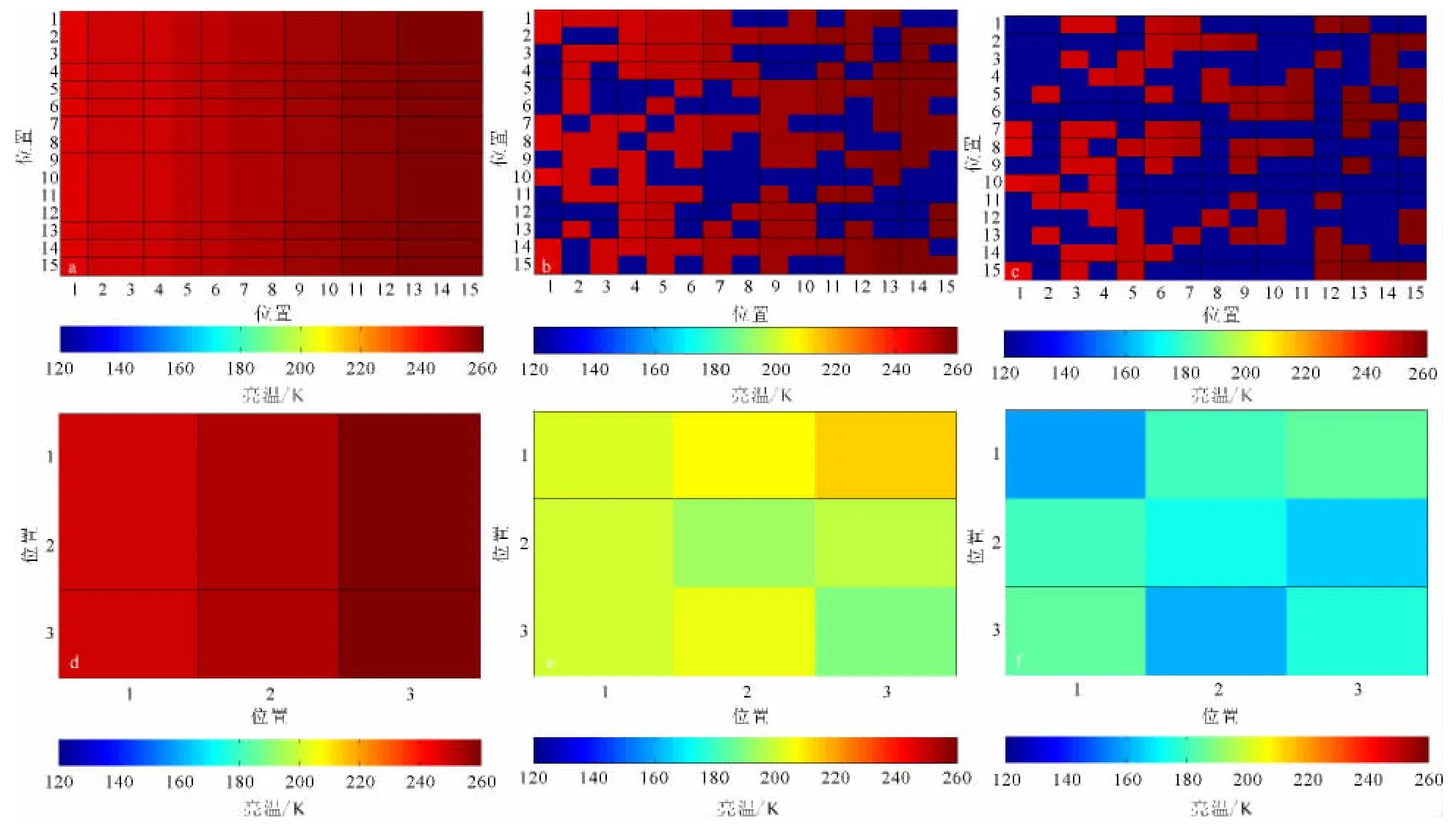
图3 方案三中组分亮温分布和混合像元亮温Fig.3 The distribution of component brightness temperature and mixed data in the third project

表1 方案三陆地组分亮温数据统计Table1 Statistics results of land component brightness temperature in the third project

表2 方案三水体组分亮温数据统计Table2 Statistics results of water component brightness temperature in the third project

3 结论与建议

1）由于陆地、水体的亮度温度差异很大，且水体亮度温度比较稳定，因此对于地物类型仅为水体和陆地2类的观测地区，若模型求解区域对应的观测地区中陆地、水体亮温组分相同，只要已知地物分类信息，无论水体的位置和比例如何变化，采用Bellerby和笔者提出的混合像元分解模型均可以从被动混合像元中准确地获得实际的水体组分和陆地组分亮温。

2）当观测地区陆地组分亮温变化时，笔者提出的方法进行混合像元分解后获得的组分亮温的精度要高于Bellerby提出的方法。笔者提出的微波混合像元分解方法中需要对于欠定方程组进行求解，其中各组分亮温的初值变化范围和条件对于求解的精度尤为重要。欠定方程组有无穷多组解，实验结果表明，如果定义好求解条件，可以从多个解中找到最优解。

3）与水体组分亮温相比，陆地上不同类型地表的亮度温度差异较大，而且观测区域内陆地类型的微波辐射亮度温度也不完全一致，这是导致目前提出的微波混合像元分解方法求解精度降低的主要原因。通过对实验结果进行分析，如果对微波混合像元中陆地类型进行再次分类，即将陆地根据地表分类数据划分为不同地表类型，进一步求得微波混合像元中多类地物的比例，建立基于多类地物分类的被动微波混合像元分解模型，通过合理定义每种类型地物组分亮温范围和设定求解约束条件，将有可能进一步提高被动微波混合像元求解的精度，这也是未来需要研究的工作。

长春净月潭遥感实验站工作人员对本文仿真实验方案设计提供了帮助和支持，谨致谢忱！

（References）：

[1]Thomas J J.Passive Microwave Remote Sensing for Land Applications[J].Earth and Environmental Science，2008（1）：9-18.

[2]尹红刚，张德海.使用BG反演算法细分重建微波辐射计图像[J].遥感技术与应用，2006，21（2）：120-124.Yin Honggang，Zhang Dehai.Subdivided Reconstruction of Microwave Radiometer Images with BG Inversion Method[J].Remote Sensing Technology and Application，2006，21（2）：120-124.

[3]Derksen C，Walker A，Ledrew E，et al.Combining SMMR and SSM／I Data for Time Series Analysis of Central North American Snow Water Equivalent[J].Journal of Hydrometeorology，2003，4（2）：304-316.

[4]Paloscia S，Macelloni G，Pampaloni P，et al.Global Scale Monitoring of Soil and Vegetation by Using AMSR-E Multi-Temporal Data [C ]／／International Geoscience and Remote Sensing Symposium（IGARSS）.Denver：IEEE，2006：1609-1612.

[5]杨虎，施建成.FY-3微波成像仪地表参数反演研究[J].遥感技术与应用，2005，20（1）：194-200.Yang Hu，Shi Jiancheng.On the Estimation of Land Surface Parameters by Using FY-3AMicrowave Radiometer Imager（MWRI）[J].Remote Sensing Technology and Application，2005，20（1）：194-200.

[6]Gu Lingjia，Zhao Kai，Zhang Shuwen，et al.Comparative Analysis of Microwave Brightness Temperature Data in Northeast China Using AMSR-E and MWRI Products[J].Chinese Geographical Science，2011，21（1）：84-93.

[7]顾玲嘉，赵凯，孙健，等.被动微波遥感数据超分辨率增强与混合像元分解研究综述[J].遥感技术与应用，2012，27（1）：25-31.Gu Lingjia，Zhao Kai，Sun Jian，et al.Review on the Super Resolution Enhancement and Unmixing Method for Passive Microwave Remote Sensing Data[J].Remote Sensing Technology and Application.2012，27（1）：25-31.

[8]Bellerby T，Taberner M，Wilmshurst A.Passive Microwave Retrieval of Ocean Surface Windspeeds for British Coastal Waters[J].IEEE Transactions on Geoscience and Remote Sensing，1999，37（5）：2578-2584.

[9]Bennartz R.On the Use of SSM／I Measurements in Coastal Regions[J].Journal of Atmospheric and Oceanic Technology，1999，16（4）：417-431.

[10]Bennartz R，Paape K，Gutman G G.Global Land Surface Characterization Using Combined Passive Microwave and Visible／Near-Infrared Satellite Data[J].Eos，Transactions，American Geophysical U-nion，1997，78（1）：59-60.

[11]Grody N C.Surface Identification Using Satellite Microwave Radiometers[J].IEEE Transactions on Geoscience and Remote Sensing，1988，26（6）：850-859.

[12]Jones A S，Vonder Haar T H.Retrieval of Microwave Surface Emittance Over Land Using Coincident Microwave and Infrared Satellite Measurements[J].Journal of Geophysical Research Atmospheres，1997，102（D12）：13609-13626.

[13]Prigent C，Rossow B W，Matthews E.Microwave Land Surface Emissivities Estimated from SSM／I Observations[J].Journal of Geophysical Research，1997，102（D18）：21867-21890.

[14]MaaB N，Kaleschke L.Improving Passive Microwave Sea Ice Concentration Algorithms for Coastal Areas：Applications to the Baltic Sea[J].Tellus Series A：Dynamic Meteorology and Oceanography，2010，62（4）：393-410.

[15]Wessel P，Smith W H F.A Global，Self-Consistent，Hierarchical，High-Resolution Shoreline Database[J].J Geophys Res：B Solid Earth，1996，101（B4）：8741-8743.

[16]Gu LingJia，Zhao Kai，Zhang Shuang，et al.An AMSR-E Data Unmixing Method for Monitoring Flood and Waterlogging Disaster[J].Chinese Geographical Science，2011，21（6）：666-675.

[17]Bellerby T，Taberner M，Wilmshurst A.Retrieval of Land and Sea Brightness Temperatures from Mixed Coastal Pixels in Passive Microwave Data[J].IEEE Transactions on Geoscience and Remote Sensing，1998，36（6）：1844-1851.

[18]Drusch M，Wood E F，Lindau R.The Impact of the SSM／I Antenna Gain Function on Land Surface Parameter Retrieval[J].Geophysical Research Letter，1999，26（23）：3481-3484.