基于BP神经网络的泥石流平均流速预测
徐黎明,王 清,陈剑平,潘玉珍
1.吉林大学建设工程学院,长春 130026
2.长江三峡勘测研究院有限公司,武汉 430073
0 引言
泥石流是全球范围内常见的一种地质灾害,多暴发于山区。我国山区面积宽广,是泥石流灾害频发的国家之一。泥石流具有突发性及流速快、流量大和破坏力强等特点。泥石流灾害的预测一直是地质灾害预测与防治的重要课题。
泥石流平均流速是泥石流动力学性质的一个基本参数,也是泥石流防治工程中不可缺少的参数[1]。准确地预测泥石流平均流速对于泥石流防治工程的设计是至关重要的。泥石流平均流速的计算方法按照泥石流的性质分为黏性和稀性泥石流计算公式两类。国外学者把泥石流简化为连续介质,建立了宾汉流体模型、膨胀流体模型、黏塑性流体模型等泥石流平均流速计算模型[2-3]。国内学者建立的公式均以曼宁公式为基础,根据泥石流流速实测数据,通过回归统计分析确定公式中待定参数的值,例如,云南东川蒋家沟泥石流流速公式[4],云南大盈江浑水沟泥石流流速公式,西藏波密古乡沟泥石流流速公式[5],甘肃武都柳弯沟、火烧沟、泥弯沟泥石流流速公式[6]等。这些经验公式都存在同样的缺点,即区域性强、普适性差,且与实测流速误差较大。
泥石流流速影响因素较多,是一个复杂的非线性系统,普通数学模型很难准确地预测泥石流流速。神经网络具有很强的非线性、自组织、自学习能力,能够很好地处理非线性信息。近年来,神经网络已广泛地应用于泥石流活动性、危险范围的预测以及泥石流的危险度评价等[7-11],但将神经网络应用于泥石流平均流速预测的研究尚较少。笔者应用BP神经网络对云南蒋家沟泥石流的平均流速实测数据进行训练和预测,建立BP神经网络的泥石流平均流速的预测模型,同时将预测结果与东川公式和文献[12]中的曼宁修正公式的计算结果进行了对比。最后将此方法应用于乌东德水电站近坝区泥石流的平均流速预测。
1 BP神经网络基本原理
人工神经网络是模仿生物神经系统的功能和结构发展起来的信息处理系统。神经元是人工神经网络的基本单元,它一般是一个多输入单输出的非线性原件[13]。一个具有r个输入分量的神经元如图1所示,其中输入分量pj(j=1,2,…,r)通过与和它相乘的权值分量wj(j=1,2,…,r)相连,求和之后形成激活函数f(·)的输入。神经元输出a除受输入信号的影响外,同时也受到神经元内部其他因素的影响,所以在人工神经网元的建模中,常常还加有一个额外输入信号b,称为偏差,也称为阈值。神经网络通过样本训练进行学习,改变内部连接的权值和阈值,使输出值与目标值误差最小,从而达到建模的目的。BP神经网络是误差反向传播多层前馈神经网络的简称。BP神经网络模型包括输入层、中间层和输出层,其结构如图2所示。BP神经网络的学习规则是最速下降法,通过误差的反向传播调整内部连接的权值和阈值,以达到减小误差的目的。网络学习过程主要由4部分组成[14]:
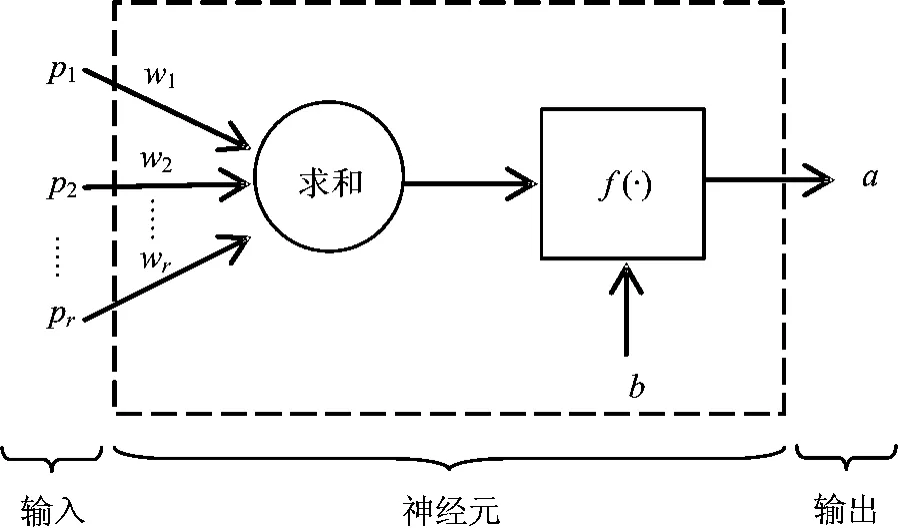
图1 神经元模型图Fig.1 Neuron model diagram

图2 BP神经网络结构示意图Fig.2 Sketch of BP neural network
1)输入模式由输入层经中间层向输出层传播计算。
2)输出的误差由输出层经中间层传向输入层。
3)模式顺传播与误差逆传播计算过程反复交替。
4)判定全局误差是否趋向极小值。
标准的BP算法收敛速度较慢,并且容易陷入局部极小值。因此各种改进的算法被提出,包括:自适应调整学习速率BP算法、动量改进BP算法、共轭梯度法、高斯牛顿法和Levenberg Marquardt法等。
2 神经网络训练与预测
2.1 确定输入因子
国内的泥石流平均流速经验公式均以曼宁公式为基础,结构形式与曼宁公式相同。曼宁公式是由爱尔兰学者Robert Manning提出的,公式如下[12]:

式中:u为平均流速,m/s;q为曼宁系数;R 为水力半径,m;J为比降。曼宁系数又称为粗糙系数,表示泥石流在运动过程中受到的阻力,受泥石流的泥沙平均粒径影响。对于宽浅的泥石流沟谷,水力半径可由泥深代替。泥石流野外调查的最大泥痕高度即为泥深。通过分析曼宁公式可知,泥石流平均流速的影响因素有泥沙平均粒径、泥深和沟床比降。泥石流是一种流体,其平均流速还会受到泥石流密度的影响。此外,泥石流的流速还会受到沟谷形态的影响,例如沟谷的卡口和跌水、沟谷的堵塞情况等。泥石流的流速随时间和空间的变化而改变。笔者对泥石流的平均流速进行预测,泥石流沟谷的卡口、跌水以及沟谷的堵塞情况仅对泥石流的局部流速产生影响,所以笔者不考虑沟谷形态对于泥石流平均流速的影响,将泥石流的泥沙平均粒径、泥深、沟床比降和泥石流的密度作为泥石流平均流速的影响因子进行泥石流平均流速的预测。这4个影响因子即为神经网络的输入因子。
2.2 训练与预测
云南省东川蒋家沟每年雨季泥石流频发,我国在东川蒋家沟设有泥石流观测站,笔者以文献[12]中蒋家沟黏性泥石流的50次观测数据为依据,进行BP神经网络的训练与预测。50次泥石流的观测数据列于表1中,前45次泥石流观测数据为训练样本,后5次泥石流观测数据为预测样本。
根据Kolmogrov定理,一个具有n个输入单元、2n+1个中间单元和m个输出单元的3层网络可以精确地表达任何映射,并且同时可以使中间层的容量和训练时间相协调[15],笔者采用该网络结构进行训练和预测。输入因子有4个,分别是泥石流的泥沙平均粒径、泥深、沟床比降和泥石流密度,输出结果为泥石流平均流速。根据Kolmogrov定理,设置网络结构为4-9-1。中间层采用tansig型激活函数,输出层采用logsig型激活函数。图3为此神经网络模型示意图,其中LW{1,1}和LW{2,1}分别代表中间层和输出层的输入分量,b{1}和b{2}分别代表中间层和输出层的偏差。初始权值和学习速率是网络训练过程中控制收敛速度的2个重要参数。选取作为初始值的量级可以达到较好的收敛速度,其中s为中间层神经元数,r为输入单元数。当学习速率是一个定值时,很难保证在训练过程中的任何训练阶段学习速率都是合适的,所以笔者采用traingda训练函数,它具有自适应调整学习速率的能力。自适应学习速率公式为


表1 蒋家沟泥石流实测数据Table1 The observation data of Jiangjiagou debris flows
其中:E为平方误差;L为学习速率。当误差小于前一次误差时,学习速率会放大1.05倍;当误差大于前一次误差的1.03倍时,学习速率则会缩小为原学习速率的60%;其他情况学习速率不变。本文中初始学习速率设为0.5,递减因子为0.6,递增因子为1.05,误差速率为1.04,目标误差设为10-4。
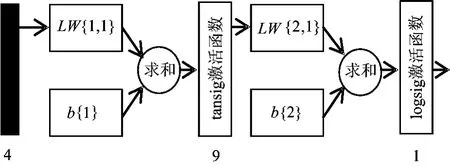
图3 BP神经网络结构图Fig.3 BP neural network model diagram
选取样本的数据大小存在差异,为了避免较小的数据被较大的数据淹没,需要对数据进行归一化处理。大多数归一化方法都是将数据归一到0~1,而网络训练中激活函数在接近0和1的时候,变化速度非常缓慢。为了提高学习速度,本文将数据归一化到0.1~0.9,按以下公式进行归一化处理:
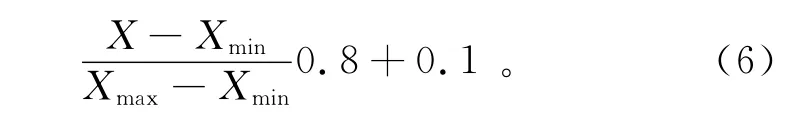
式中:X为输入因子的指标值;Xmin和Xmax分别为指标值中的最大值和最小值。
BP神经网络设置完毕和数据归一化处理之后即可进行网络训练;训练收敛之后,对预测样本进行泥石流平均流速的预测。将预测结果与东川公式和文献[12]中的曼宁修正公式的计算结果进行比较,对比结果列于表2中。
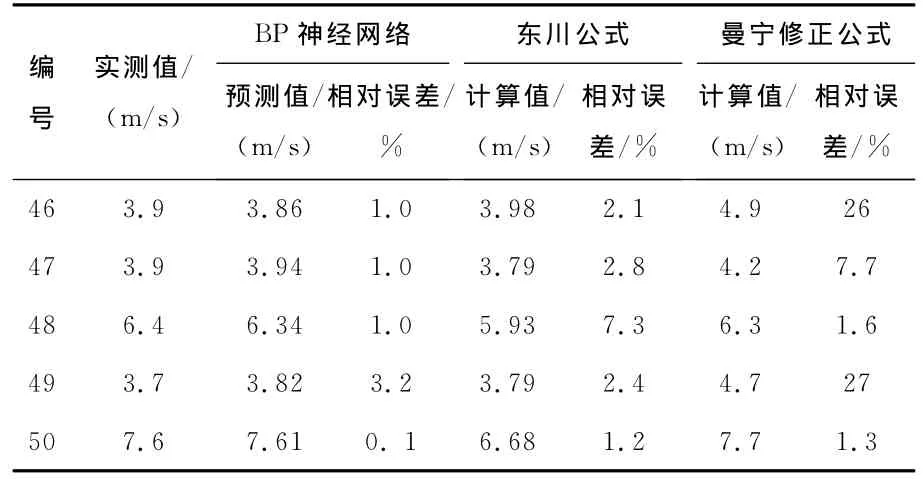
表2 泥石流平均流速预测结果对比Table2 The contrast of forecast mean velocities of debris flows
东川公式是以曼宁公式为基础、以东川地区的泥石流观测数据为依据建立的泥石流平均流速计算公式,适用于东川地区的泥石流,其精度明显高于曼宁修正公式。从表2中可以看出:东川公式计算结果的最小误差为1.2%,最大误差为7.3%;BP神经网络的预测结果的最小误差仅0.1%,最大误差3.2%;总体上,其精度比东川公式稍高一些。3种对比方法中,BP神经网络的预测结果精度最高。
3 实例计算
乌东德水电站位于金沙江下游,设计装机容量7 400MW,水库库区内发育大量泥石流,尤其是近坝区内发育的下白滩、上白滩和猪拱地3条泥石流沟会对水电站的正常建设和运行造成严重的威胁。这3条泥石流沟的泥石流平均流速是进行泥石流防治工程设计的重要参数。
由于本文中的训练样本均为黏性泥石流,所以此模型仅适用于黏性泥石流平均流速的预测。经过野外现场调查,并依据《泥石流灾害防治工程勘查规范》DZ/T 0220-2006[16]判断这3条沟的泥石流均为黏性泥石流,与训练样本属于同一区域,所以可以应用BP神经网络预测模型对这3条沟的泥石流平均流速进行预测。通过详细的现场调查和室内试验获取的泥石流泥沙平均粒径、泥深、沟床比降和泥石流密度数据如表3所示。
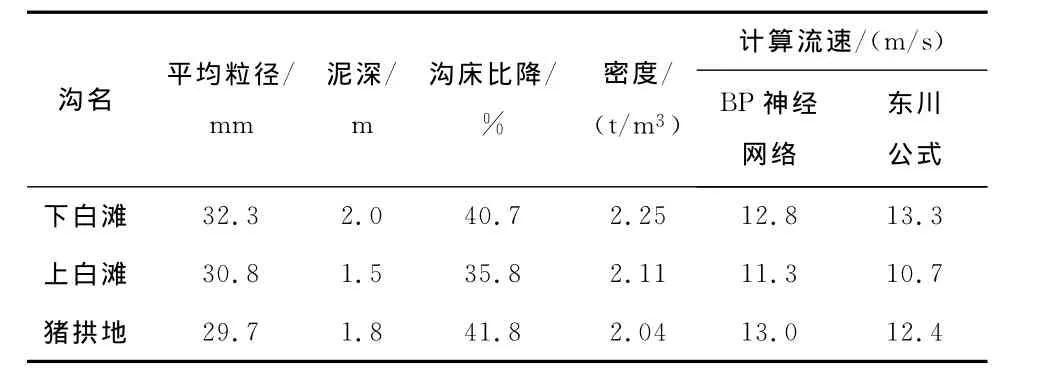
表3 泥石流调查结果Table3 The investigation results of debris flows
应用BP神经网络对这3条沟的泥石流平均流速预测结果分别为12.8、11.3和13.0m/s;采用东川公式计算这3条沟的泥石流平均流速分别为13.3、10.7和12.4m/s,计算结果已列入表3中。BP神经网络的平均流速预测结果与东川公式的计算结果基本相同,最大相差仅0.6m/s,可见此方法可为泥石流的防治设计提供可靠的参数。BP神经网络预测方法与东川公式相比,其最大的优点在于普适性强。东川公式仅适用于东川地区的泥石流,计算其他地区的泥石流平均流速时误差会较大,而BP神经网络预测方法则可以通过训练其他地区的观测数据,建立适应于其他地区的预测模型来预测泥石流的平均流速,并且预测精度比较高。以实测数据作为训练样本是BP神经网络预测泥石流流速的基础,所以此方法基本前提是获得预测地区的泥石流流速实测数据。当不同的泥石流多发地建立起泥石流数据库时,BP神经网络预测方法的普适性可以得到充分的发挥。
综上所述,将BP神经网络应用于泥石流平均流速的预测是切实可行的。此方法的优点在于普适性强、准确度较高;其缺点在于需要大量的预测地区的泥石流流速实测数据,并且实测的泥石流要与预测的泥石流类型一致。只要获得与预测的泥石流属同一地区、且类型一致的泥石流流速实测数据,此方法可适用于任何地区泥石流的平均流速预测。
4 结论
1)应用BP神经网络预测泥石流的平均流速切实可行。
2)以泥石流的泥沙平均粒径、泥深、沟床比降和泥石流密度作为泥石流平均流速的影响因素,通过对云南东川蒋家沟泥石流的观测数据进行训练与预测建立的泥石流平均流速的BP神经网络预测模型最大误差仅为3.2%,曼宁修正公式和东川公式最大误差分别为27%和7.3%。BP神经网络模型对泥石流平均流速预测精度最高。
3)BP神经网络模型可以通过对不同地区的泥石流观测数据进行训练与预测,建立适用于不同地区的泥石流平均流速预测模型,此方法具有一定的普适性。
4)泥石流实测数据是建立BP神经网络模型的基础,建立不同的泥石流多发地区的泥石流数据库具有很重要的意义,可为当地泥石流平均流速的预测提供可靠的依据。
(References):
[1]刘丽,陈洪凯.泥石流运动力学研究现状及趋势[J].重庆交通大学学报:自然科学版,2010,29(2):233-239.Liu Li,Chen Hongkai.Research Status and Trend About Dynamics of Debris Flow [J].Journal of Chongqing Jiaotong University: Natural Science,2010,29(2):233-239.
[2]黄芮.基于PPA的乌东德水电站库区泥石流流速模型建立与计算[D].长春:吉林大学,2011.Huang Rui.Model Building and Calculation of the Debris Flow Rate in Dam Site of Wudongde Hydropower Station Based on PPA[D].Changchun:Jilin University,2011.
[3]柴春岭,陈守煜.模糊优选神经网络模型在泥石流平均流速预测中的应用研究[J].大连理工大学学报,2008,48(6):887-891.Chai Chunling,Chen Shouyu.Research on Application of Fuzzy Optimization Neural Network Model to Debris Flow Average Velocity Forecasting[J].Journal of Dalian University of Technology,2008,48(6):887-891.
[4]吴积善,康志成,田连权,等.云南蒋家沟泥石流观测研究[M].北京:科学出版社,1990.Wu Jishan,Kang Zhicheng,Tian Lianquan,et al.Study on Observation of Jiangjiagou Debris Flows in Yunnan Province[M].Beijing:Science Press,1990.
[5]程尊兰,刘雷激.西藏古乡沟泥石流流速[J].山地研究,1997,15(4):293-295.Cheng Zunlan,Liu Leiji.Debris Flow Velocity of Guxiang Ravine,Xizang[J].Journal of Mountain Research,1997,15(4):293-295.
[6]中国科学院兰州冰川冻土研究所,甘肃省交通科学研究所.甘肃泥石流[M].北京:人民交通出版社,1982.Lanzhou Institute of Glaciology and Cryopedology,Chinese Academy of Sciences,Gansu Communications Science Research Institute.Gansu Debris Flow[M].Beijing:China Communications Press,1982.
[7]鲁小兵,李德基.基于神经网络的泥石流预测[J].自然灾害学报,1996,5(3):47-50.Lu Xiaobing,Li Deji.Debris Flow Forecast Based on Neural Net[J].Journal of Natural Disasters,1996,5(3):47-50.
[8]汪明武.基于神经网络的泥石流危险度区划[J].水文地质工程地质,2000(2):18-19.Wang Mingwu.Classification of Dangerous Degree of Debris Flow Based on Neural Network [J].Hydrogeology and Engineering Geology,2000(2):18-19.
[9]李发斌,崔鹏,周万村,等.用遗传神经网络分析泥石流活动性[J].中国地质灾害与防治学报,2003,14(3):16-20.Li Fabin,Cui Peng,Zhou Wancun,et al.Activity Analysis of Debris Flow Using Genetic Neural Network[J].The Chinese Journal of Geological Hazard and Control,2003,14(3):16-20.
[10]张晨,王清,张文,等.基于神经网络对泥石流危险范围的研究[J].哈尔滨工业大学学报,2010,42(10):1642-1645.Zhang Chen, Wang Qing,Zhang Wen,et al.Prediction on Hazardous Areas of Debris Flow Based on Neural Network[J].Journal of Harbin Institute of Technology,2010,42(10):1642-1645.
[11]Chang Tungchiung.Risk Degree of Debris Flow Applying Neural Networks[J].Natural Hazards,2007,42:209-224.
[12]徐永年.崩塌土流动化机理及泥石流冲淤特性的实验研究[D].北京:中国水利水电科学研究院,2001.Xu Yongnian.Study on Flow Mechanism for Avalanche Soils and Scour and Silting Characteristics of Debris Flows[D].Beijing:Institute of Water Conservancy and Hydroelectric Power Research,2001.
[13]丛爽.面向matlab工具箱的神经网络理论与应用[M].合肥:中国科学技术大学出版社,1998.Cong Shuang.Neural Network Theory and Applications with Matlab Toolboxes[M].Hefei:University of Science and Technology of China Press,1998.
[14]肖云华.双峰隧道围岩稳定性非线性系统研究[D].长春:吉林大学,2009.Xiao Yunhua.Nonlinear Systemic Study on the Stability of Surrounding Rock of Shuangfeng Freeway Tunnel[D].Changchun:Jilin University,2009.
[15]张晨,陈剑平,肖云华.基于神经网络对有限元强度折减法分析[J].吉林大学学报:地球科学版,2009,39(1):114-118.Zhang Chen,Chen Jianping,Xiao Yunhua.Analysis on Theory of Strength Reduction FEM Based on Artificial Neural Networks[J].Journal of Jilin University:Earth Science Edition ,2009,39(1):114-118.
[16]DZ/T 0220-2006泥石流灾害防治工程勘查规范[S].北京:中国标准出版社,2006.DZ/T 0220 - 2006Specification of Geological Investigation for Debrits Flow Stabiliation[S].Beijing:Standards Press of China,2006.

