异步牵引电机全速域直接转矩控制仿真研究

，，

（西南交通大学 电气工程学院，四川 成都 610031）

1 引言

牵引传动系统控制策略的选择是决定其性能优劣的关键因素[1]。直接转矩控制（DTC）技术作为一种高性能交流调速技术，在高速列车主传动等大功率系统中得到了广泛应用。与矢量控制相比，直接转矩控制具有更优的动态响应能力，且无需复杂的坐标变换，控制目标更加明确[2-4]。同时，由于在估算磁链和转矩时，只需要电机定子侧参数，因此其对电机参数的依赖性相对于矢量控制有所减弱[5]。但传统直接转矩控制系统的开关频率并不固定，不能充分利用变流器的开关资源[1]。文献[6-7]采用直接转矩控制与矢量调制相结合的方式实现了开关频率的近似恒定。文献[8]则通过一个转矩控制器来代替传统的三态滞环比较器，也达到了降低开关频率的目的。

本文针对异步电机的牵引特性，将电力牵引运行分成3个调节区域，重点研究了前2个调节区域，设计了在不同速度区域内能近似恒定开关频率的直接转矩控制算法，并采取有效的算法切换过渡措施，实现了算法间磁链和转矩的无跳变切换，建立起全速域直接转矩控制的仿真模型，实现了恒转矩区和恒功率区的调节。

2 全速域直接转矩控制算法设计

通常情况下，电力牵引运行可分为3个运行调节区［9］：启动加速区（恒转矩区）、恒功率输出区和提高速度区或自然特性区，如图1所示。

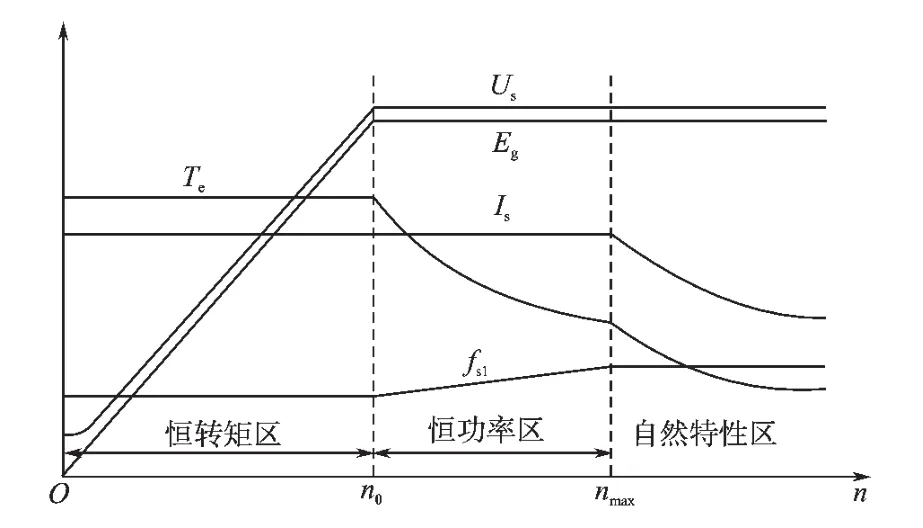
图1 电力牵引特性曲线Fig.1 The characteristic curves of electric traction system

恒转矩区（基速n0以下范围）。在该区域保持气隙磁通近似不变，电动机可以在任何速度下发挥较大转矩，通过控制转差频率为固定值，即可使得牵引电机在恒转矩下工作。在恒转矩区的低速域，采用改进的圆形磁链轨迹DTC控制方式；在恒转矩区的中速域，采用十八边形磁链轨迹DTC控制方式；在恒转矩区的高速域，采用六边形磁链轨迹DTC控制方式。

恒功率区或弱磁范围 I（n0＜n＜nmax）。 随着电机转速的上升，电压Us提高，电机的输出功率增大，但是电压的提高受到电机功率或逆变器最大电压的限制，当电机的定子电压接近于电机反电势时，电压不再能够继续升高，导致电机转速受限。为了能够进一步提高传动系统的转速，使其能够运行于基速以上范围，采取削弱磁通的方式来降低反电势，牵引电动机在这一过程中运行于恒功率区。在恒功率区中，采用方波DTC控制方式。

2.1 低速域直接转矩控制算法

传统基于开关表的圆形磁链DTC中，系统具有开关频率不固定，电流正弦性差，谐波含量高，转矩脉动大的缺点。为解决上述问题，本文采用基于空间矢量脉宽调制的直接转矩控制 （SVMDTC）方式[10]，该方案基于定子两相αβ静止坐标系，由转矩和磁链求得下一时刻需要施加的定子电压矢量，再将该矢量经过空间矢量调制得到所需开关信号，其控制过程如图2所示。

图2 SVM-DTC控制系统框图Fig.2 The block diagram of SVM-DTC control system

SVM-DTC控制方式是将电磁转矩设定值与反馈值之差通过PI调节器，其输出可定义为消除转矩误差所需的角度差△xd，由于在控制过程中定子磁链会继续向前运动，其在一个控制周期内走过的电角度表示为△xσ，将二者叠加，即可得到下一控制周期磁链需要走过的角度。同时，将磁链设定值与反馈值之差通过PI调节器，其输出可定义为下一周期磁链增量系数KΨ，再根据磁链目标值，并结合磁链方程，可求出作用在逆变器上的电压矢量：

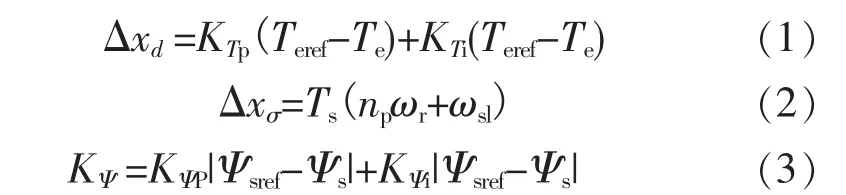
式中：ωsl为转差转速，ωsl=2TeRr/3np|Ψs|2；Teref，Te分别为给定转矩和估算转矩；Ψsref，Ψs分别为给定磁链和估算磁链；Ts，np，ωr分别为控制周期、电机极对数及转子转速。

假设当前控制周期的定子磁通角度为θ，若下一控制周期能使定子磁链达到给定磁链，则：

那么在控制周期内定子磁链的增量△Ψs为

假如控制周期Ts足够短，则有下式成立：

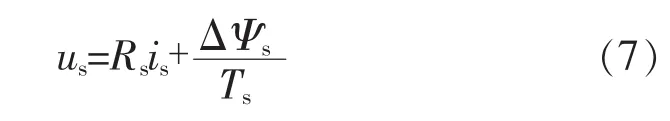
由此，可得到参考电压矢量为

其中，usαref，usβref包含了下一周期所希望得到的 转矩和磁链信息，将该参考电压矢量进行空间矢量调制，就可以得到逆变器的门极脉冲。

2.2 中高速域直接转矩控制算法

当电机转速上升时，逆变器开关频率随之上升，零电压作用时间与次数大大减少，定子电压的平均值比较大，定子电阻压降的影响也可以忽略。为降低开关损耗，并且充分地利用直流侧电压，在中高速范围内采用多边形磁链轨迹DTC控制方式，其系统控制结构如图3所示。

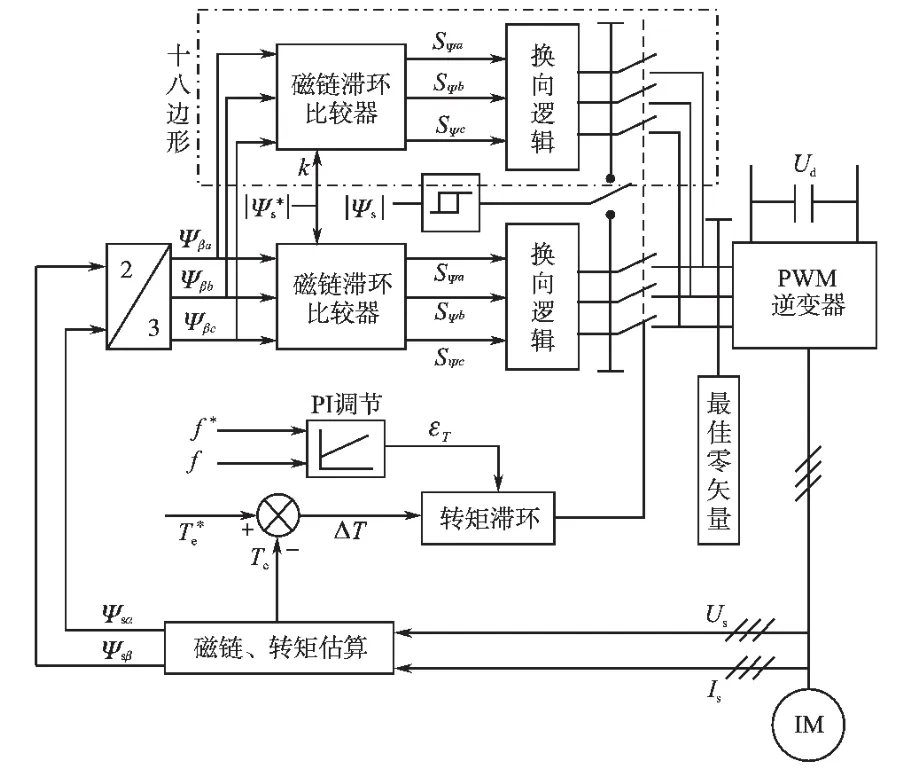
图3 中高速域直接转矩控制系统框图Fig.3 The block diagram of DTC system in mediumhigh speed range

在15%n0～85%n0范围内，采用十八边形磁链轨迹直接转矩控制方式。它是在正六边形的基础上，对其进行折角处理，使定子磁链运行于内、外正六边形上，得到接近于圆形的十八边形磁链轨迹，如图4所示。此种控制方式不仅简单易行，而且具有较高的磁通利用率，当选择特定的折角时，还能够消除特定次数的谐波，其详细分析过程见文献[11]。

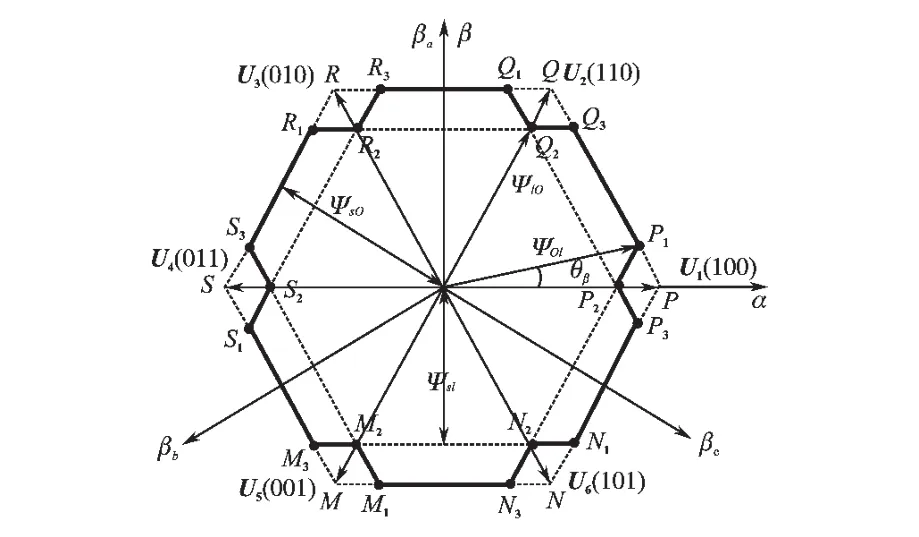
图4 十八边形磁链轨迹图Fig.4 The locus diagram of octadecagon flux

在85%n0～100%n0范围内，采用六边形磁链轨迹直接转矩控制方式。它是在每一个扇区，只采用一种有效矢量和一种零矢量来实现对电机的控制，因此其磁链轨迹为正六边形，如图5所示。此种控制方式不仅结构简单，而且能够充分地利用直流侧电压。

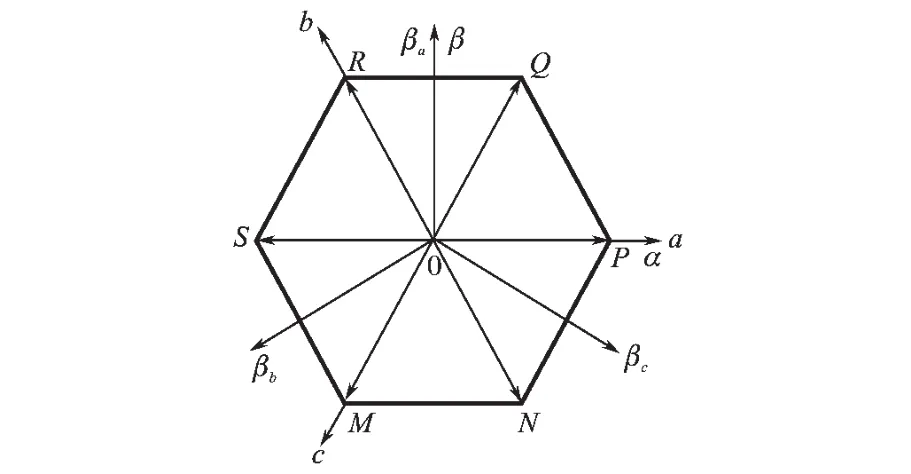
图5 六边形磁链轨迹图Fig.5 The locus diagram of hexagon flux

由于多边形磁链轨迹直接转矩控制的开关频率仍旧不固定，导致开关损耗不均匀。为了能近似恒定逆变器开关频率，在控制系统中，引入了频率调节器，通过调节转矩滞环的容差，达到实际频率跟踪给定频率的目的。

2.3 弱磁高速域直接转矩控制算法

当电机的转速达到基速（n0）时，传动系统不再能够继续增加转速，因为电机的定子电压已经接近反电动势的大小，此时，需通过降低定子磁链幅值来限制反电势的大小，从而达到提高转速的目的。在DTC控制系统中直接控制定子磁链的幅值给定，便可以实现弱磁功能，控制系统框图如图6所示。

图6 弱磁方波控制系统框图Fig.6 The block diagram based on square wave control

电机进入弱磁域运行时，磁链轨迹依然是六边形，但在基速域起作用的零矢量会退出控制，工作电压为6个有效电压矢量，定子磁链将会以最大速度旋转，此时，转矩的调节是依靠功率PI和动态磁弱PI共同作用来实现的[1]。

2.4 不同DTC控制算法仿真

根据不同速度域的控制算法，分别搭建直接转矩控制系统的仿真模型，SVM-DTC控制仿真结果如图7所示；十八边形磁链DTC控制仿真结果如图8所示；六边形磁链DTC控制仿真结果如图9所示；弱磁方波控制仿真结果如图10所示。

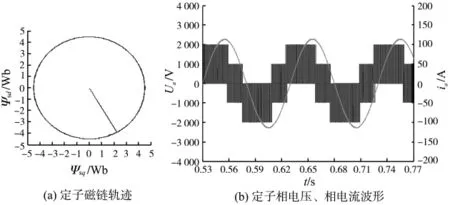
图7 SVM-DTC直接转矩控制仿真波形Fig.7 The simulation waveforms of SVM-DTC

图8 十八边形磁链轨迹直接转矩控制仿真波形Fig.8 The simulation waveforms of DTC with octadecagon flux

图9 六边形磁链轨迹直接转矩控制仿真波形Fig.9 The simulation waveforms of DTC with hexagon flux

图10 弱磁方波控制仿真波形Fig.10 The simulation waveforms of square wave control

3 DTC控制算法切换过渡措施

在直接转矩控制系统中，由于不同速度域采用不同的磁链轨迹控制方式，因此，在不同速度域间需要对算法进行切换，为了使不同算法能够顺利切换而不引起转矩和磁链的跳变，采用速度滞环和等磁链幅值的切换措施。

采用滞环切换代替速度点切换，目的是防止因速度波动而导致算法间的频繁切换。当速度进入速度滞环内时，并不急于切换，而是同时运行相邻速度域的两种控制算法。当磁链在β坐标系下的任一分量幅值与圆形磁链幅值相等时，完成圆形控制与十八边形控制切换，考虑到磁链位置的可确定性，只在图 12 中的 A，B，C，D，E，F 6 个点附近发生切换；当磁链在β坐标系下的任一分量幅值与外六边形滞环容差值相等时，完成十八边形控制与六边形控制切换。不同算法切换点示意图如图11所示。

图11 不同算法切换点示意图Fig.11 The diagram of diverse algorithms switching point

4 全速域DTC控制仿真与分析

DTC控制系统中所采用电机参数为：额定功率562 kW，额定线电压2 700 V，额定电流145 A，最高转速 5 900 r/min，额定转速 4 100 r/min，定子电阻0.113 5 Ω，定子漏感1.41 mH，转子电阻0.072 3 Ω，转子漏感 1.85 mH，互感 52.62 mH，极对数2。

中间直流侧电压设定为3 000 V，为了减少仿真时间，设置转动惯量为5 kg·m2。

为模拟高速列车实际运行过程，仿真设计如下：t=0 s时，给定转速为n*=5 000 r/min(相当于高速列车运行速度v*=311 km/h)；t=3 s时，给定转速为3 000 r/min(相当于高速列车运行速度v*=186 km/h)；t=5 s时，高速列车上i=1.5%的坡道。DTC控制系统仿真结果如图12所示。

图12 全速域直接转矩控制仿真波形Fig.12 Simulation waves of DTC in full speed range

由仿真结果可知，在基速域（恒转矩区），逆变器按脉宽调制方式工作，3种不同磁链轨迹的直接转矩控制方式控制效果良好，并且实现了控制方式的平滑过渡，没有出现大的磁链畸变；从恒转矩区进入恒功区阶段，由相电压波形可知，作用于逆变器的零电压矢量变少，完全进入恒功区后，零电压矢量退出作用；当完全进入恒功区后，定子磁链随转速上升而减小，系统按弱磁域特点运行，此时电机的输出功率恒定，转矩与速度基本成反比关系，转速的上升变缓。当牵引异步电机转速从5 000 r/min下降到3 000 r/min的过程中，系统从牵引工况转换进入制动工况，电机功率及转矩均变为负值。当列车进入1.5%的坡道时，控制系统依然能够保证列车稳定运行。

5 结论

本文根据异步牵引电机的特性，研究了一套适合于异步牵引电机的全速域直接转矩控制算法，采用空间矢量调制及PI频率调节器的方式近似恒定了逆变器开关频率，同时，引入算法过渡切换措施完成了磁链和转矩的无跳变切换。最后采用高速列车的数据作为仿真参数，对全速域直接转矩控制系统进行仿真建模，仿真结果验证了该控制系统能够满足高速列车的基本运行特性。

［1］冯晓云.电力牵引交流传动及其控制系统［M］.北京：高等教育出版社，2009.

［2］齐永龙.异步电机直接转矩控制系统的研究［D］.成都：西南交通大学，2003.

［3］张令霞，张兴华.直接转矩控制系统的Matlab建模与仿真［J］.电气传动，2011，41（1）：9－13.

［4］廖晓钟，邵立伟.直接转矩控制的十二区段控制方法［J］.中国电机工程学报，2006，26（6）： 167－173.

［5］Takahashi I，Noguchi T.A New Quick-response and Highefficiency Control Strategy of an Induction Motor［J］.IEEE Transactions on Industry Applications， 1986， 22（5）： 820－827.

［6］祝龙记.基于空间矢量PWM的新型直接转矩控制系统［J］.电气传动，2005，35（4）：11－13.

［7］宋昌林，唐浦华，李治.具有恒定开关频率的感应电机无速度传感器直接转矩控制［J］.铁道学报，2004，26（1）：49－53.

［8］钱坤，谢寿生，高梅艳，等.改进的直接转矩在异步电动机中的应用［J］.中国电机工程学报，2004，24（7）：210－214.

［9］Pham Vantien，冯晓云，Do Vietdung，等.异步电机牵引特性的仿真研究［J］.电气传动，2009，39（5）：24－26.

［10］袁登科，陶桂生.一种感应电机直接转矩控制系统性能改善方案［J］.中国电机工程学报，2005，25（8）：151－155.

［11］倪大成，年晓红，刘可安.十八边形磁链直接转矩控制算法设计及实现［J］.铁道学报，2008，30（2）：28－33.