用扩展的Istomin-Palm 模型估算双向延伸化合物R1-Y-R2生成焓
曹晨忠 武亚新
(1湖南科技大学化学化工学院,理论化学与分子模拟教育部重点实验室,分子构效关系湖南省普通高校重点实验室,湖南湘潭411201;2中南大学化学化工学院,长沙410083)
1 Introduction
As one of the most important thermodynamic parameters,the enthalpy of formation ΔfH0plays an important role in the chemical research.For lack of available experimental data,the accurate calculation of the ΔfH0by theoretical method has attracted more and more attention.1-13Previous research indicated that the effect of the interactions among bonding and non-bonding atoms or groups on the ΔfH0for organic compounds is very obvious,and can not be neglected in the calculation process.14-19Ju et al.16reported that the interacting energies(in the range of 14-20 kJ·mol-1)from neighbor difluoroamino groups discorded with the group additivity in calculating the ΔfH0for polydifluoroaminocubanes.Mathieu18proved that the introduction of pairwise interactions between geminal atoms and adjacent bonds in strained rings dramatically improved the performance of simple bond additivity schemes for ΔfH0prediction.Above reported works imply that,to obtain more reliable values of enthalpies of formation,the contributions of the interactions among the component atoms or groups must be taken into account for.
For monoderivatives of hydrocarbons RX,their enthalpies of formation can be divided into three parts,and expressed by Eq.(1)(i.e.,Istomin-Palm model).20
ΔfH0(RX)=h[R]+h[X]+φ[R]φ[X] (1)In Eq.(1),the h[R]and h[X]are the contributions of alkyl R and substituent X to the ΔfH0(RX),respectively.φ[R]φ[X]represents the interaction of alkyl R and substituent X.Cao et al.21-23has employed the product of the electronegativity(χ)of the radical atom of substituent X and the polarizability effect index(PEI)or topological electronegativity index(TEI)of the alkyl R to roughly scale the interaction between the R and X(φ[R]φ[X]).It is noted that the χ of the radical atom can not distinguish those substituents whose radical atom is the same(such as the couple of―CHO and―COOH,or the couple of―NH2and―NO2).However,it is commonly believed that the structural characteristic and influence on the molecular properties of each couple of groups are different.Thus,in our recent work,24a new concept of interaction potential index IPI(X)was proposed to scale the interaction potential of the X with an alkyl,and the IPI(X)values of 16 kinds of groups(X=OH,SH,NH2,Br,Cl,I,NO2,CN,CHO,COOH,CH3,CH=CH2,C≡CH,Ph,COCH3,COOCH3)were obtained,with which a more effective model was developed for evaluating the ΔfH0(g)values of monosubstituted alkanes RX(including the branched derivatives).
With respect to the two-direction extending compounds R1-Y-R2,the substituents(Y)are in the middle of the molecular chain and attached by two alkyl groups(R1,R2).Their intramolecular interactions among the substituent and alkyls are more complicated than that in the RX.Thus,the item φ[R]φ[X]of Eq.(1)is unavailable.In this paper,the intramolecular interactions among the Y,R1,and R2 are investigated,and a general expression is derived to describe the enthalpies of formation of R1-Y-R2.
2 Method
In general,we think,the interactions among Y,R1,and R2 in the compounds R1-Y-R2 should be divided into three parts:the interaction between R1Y and R2(φ[R2]φ[R1Y]),the interaction between YR2 and R1(φ[R1]φ[YR2]),and the interaction between R1 and R2(ψ[R1]ψ[R2]).Therefore,Eq.(1)can be extended as Eq.(2)to express the enthalpies of formation of R1-Y-R2.
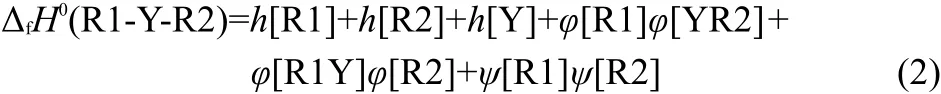
In Eq.(2),the h[Y]is the contribution of substituent Y to the ΔfH0.The h[R1]and h[R2]are the contributions of alkyls R1 and R2 to the ΔfH0,respectively.The last three items are the total contribution of interactions among the Y,R1,and R2 to the ΔfH0.
According to our previous studies,21-24the h[R1],h[R2],φ[R1],and φ[R2]can be scaled by Eqs.(3)to(6),respectively.

In Eqs.(3)to(6),the c and d are coefficients,the NC(R1)and NC(R2)are the C atom number of alkyls R1 and R2,respectively.The PEI(R)indicates the polarizability effect index of group R,which is proposed on the basis of the principle that groups are polarized by electric fields.25,26The ΔPEI(R)is the increment of PEI(R)of the branched alkyl to that of its isomeric straightchain alkyl.24
The h[X]in Eq.(1)has a good correlation with the experimental ΔfH0values of monosubstituted methane ΔfH0(MeX).24Similarly,it can be considered that there is a good correlation between the h[Y]in Eq.(2)and the experimental value of ΔfH0(Me-Y-Me).Thus,the Eq.(7)can be used to scale the h[Y].

In Eq.(7),the a and b are coefficients.
In common believe,the action of group R1Y on R2(i.e.,φ[R1Y])is not only related to the intrinsic action of subsitituent Y on an alkyl(i.e.,φ[Y]),but also affected by the alkyl(R1)connected to Y.Therefore,the φ[R1Y]can be expressed as

where q is a coefficient,and the φ[R1]φ[Y]represents the influence of R1 on the subsitituent Y.Similarly,the action of group YR2 on R1(i.e.,φ[YR2])can be expressed as

In our previous work,24in case X groups are OH,SH,NH2,and CHO,the φ[X]can be scaled by the interaction potential of the X with an alkyl,which is defined as the interaction potential index IPI(X).Thus,for the Y groups O,S,NH,and CO,the YH are OH,SH,NH2,and CHO,that is to say,YH corresponds to its X,and it can be speculated that the IPI(Y)is proportional to the IPI(X),
φ[Y]=IPI(Y)=eIPI(X) (10)In Eq.(10),the e is a coefficient.Combining Eqs.(5,6,10)with Eqs.(8,9),we obtained the expressions of φ[R1Y]and φ[YR2]respectively.

In general,it is considered that the interaction of R1 and R2 is mainly affected by steric effects.In the present work,the last item ψ[R1]ψ[R2]in Eq.(2)is expressed by the product of ΔTSEI(R1)and ΔTSEI(R2),

In Eq.(13),the g is a coefficient.The ΔTSEI(R)is the increment of topological steric effect index27of the branched alkyl to that of its isomeric straight-chain alkyl,and can be calculated as shown in Eq.(14).
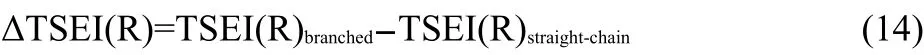
Take group t-Bu for a calculation example,its ΔTSEI(R)is,
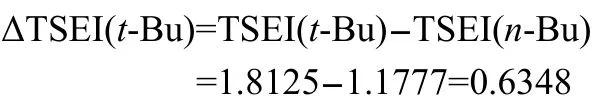
Combining Eqs.(3-13)with Eq.(2),we obtained the expression of the ΔfH0(R1-Y-R2),
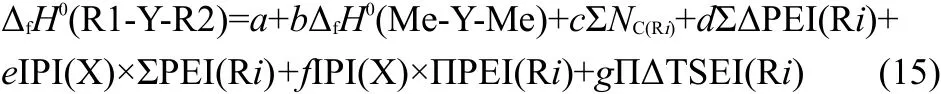
where f is a coefficient,that is f=-2e×q.The detailed meanings of the parameters in Eq.(15)are as follows,
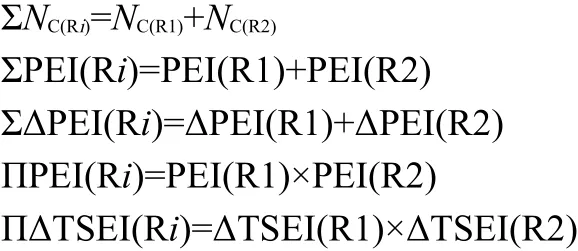
For the esters R1C(O)OR2,its R1 is attached to the C atom and R2 to the O atom.It implies that the intrinsic action of group C(O)O(φ[C(O)O])on alkyls R1 and R2 is different from each other.Therefore,Eqs.(11,12)are revised as Eqs.(16,17)to express the action of R1C(O)O on R2(i.e.,φ[R1C(O)O])and the action of C(O)OR2 on R1(i.e.,φ[C(O)OR2]),respectively.
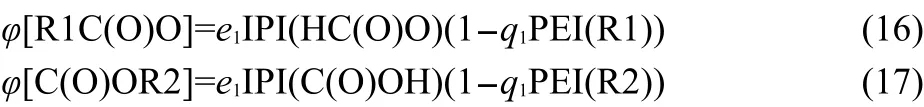
Based on the above analyses,Eq.(15)can be expanded as Eq.(18a)to express ΔfH0of esters R1COOR2.
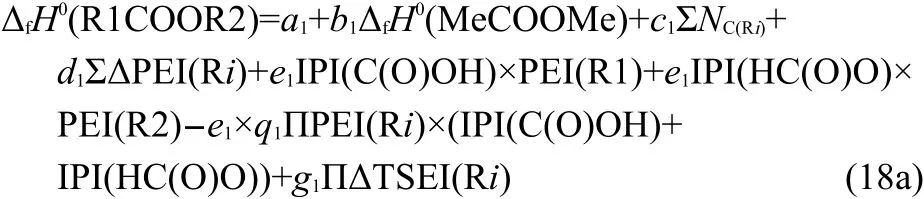
In Eq.(18a),theΔfH0(MeCOOMe),IPI(C(O)OH),and IPI(HC(O)O)are constants.Therefore,Eq.(18a)can be simplified to Eq.(18b),
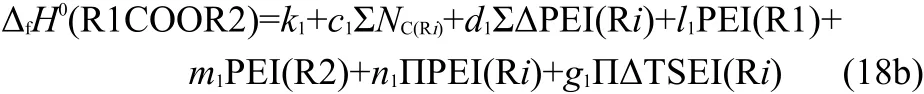

Table 1 Interrelation of ΔfH0(Me-Y-Me),ΣNC(Ri),ΣΔPEI(Ri),IPI(X),ΠPEI(Ri),ΠΔTSEI(Ri),PEI(R1),and PEI(R2)
where k1,l1,m1,and n1are coefficients,that is
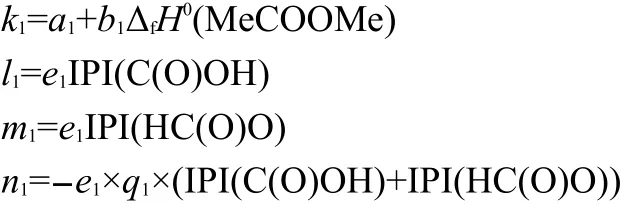
The correlations between these parameters ΔfH0(Me-Y-Me),,ΣΔPEI(Ri),IPI(X),ΠPEI(Ri),ΠΔTSEI(Ri),PEI(R1),and PEI(R2)were investigated.Results of Table 1 show that these 8 parameters of 81 two-direction extending compounds R1-Y-R2(Y=S,NH,O,CO,C(O)O)are independent of each other.
3 Results and discussion
3.1 Predicting the ΔfH0of thioether,secondary amines,ethers,and ketones
To test the efficiency of Eq.(15),we took 54 experimental(g)values13,28,29of R1-Y-R2(Y=S,NH,O,CO)as a data set(see Table 2 and Table 3),and carry out a regression analysis with the six parameters,ΔfH0(Me-Y-Me,g),ΣNC(Ri),ΣΔPEI(Ri),IPI(X)×ΣPEI(Ri),IPI(X)×ΠPEI(Ri),and ΠΔTSEI(Ri).The result was shown as Eq.(19).

Table 2 Calculated and experimental values of ΔfH0(g)of R1-Y-R2(Y=S,NH,O,CO)
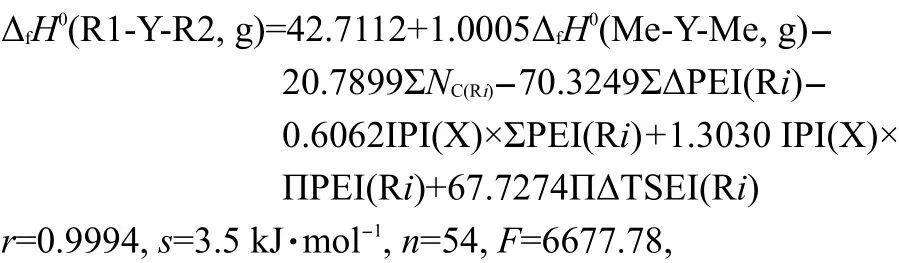
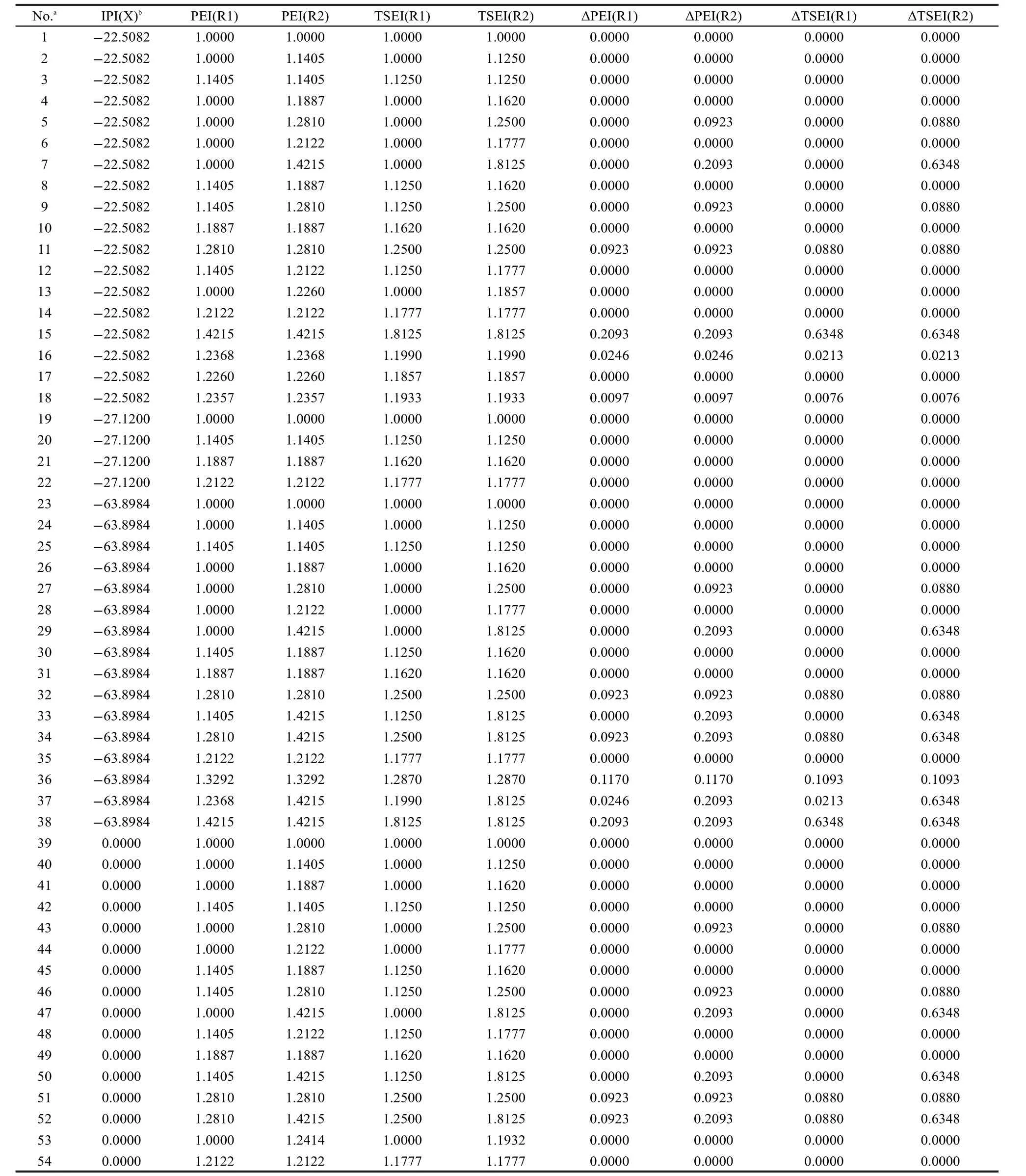
Table 3 IPI,PEI,TSEI,ΔPEI,and ΔTSEI values of R1 and R2 in R1-Y-R2(Y=S,NH,O,CO)

Fig.1 Plot of ΔfH0(g)calc.calculated with Eq.(19)vs ΔfH0(g)exp.

where the statistics r,s,F,and n represent the correlation coefficient,the standard deviation of the linear regression,Fischer criterion,and the sample numbers,respectively.The rcvand scvare the correlation coefficient and standard deviation calculated by leave-one-out(LOO)method.Eq.(19)has a good correlation(see Fig.1).The average absolute error between the experimental values and the calculated values is only 2.6 kJ·mol-1,within the experimental uncertainties.The coefficient in front20.7899,indicates the contribution of each CH2unit to the ΔfH0(g).Its value is very close to the value,-20.69,derived from the straight-chain alkanes.24This implys that the group contribution of a CH2unit obtained by Eq.(19)is reasonable and accurate.The results of leave-one-out(LOO)method(rcv=0.9989,scv=4.6 kJ·mol-1)confirm the stability of Eq.(19).The above results proved that Eq.(15)is an effective model for estimating the ΔfH0(g)of thioether,secondary amines,ethers,and ketones.In this work,Eq.(19)is also employed to predict the ΔfH0(g)of over 500 compounds,and these predicted values are given in the Supporting Information.
3.2 Comparison with G3 and G3B3 model chemistries
Bond13proposed that the enthalpies of formation for nitrogen-,oxygen-,sulfur-,fluorine-,chlorine-,and silicon-containing compounds can be computed with reasonable accuracy using the G3 and G3MP2 model chemistries.The calculated ΔfH0(g)values of four kinds of compounds including thioether,secondary amines,ethers,and ketones with Eq.(19)and those calculated by G3 and G3MP2 model chemistries are all given in Table 2.Their average absolute errors between the experimental and the calculated values using G3 model are 2.7,2.9,4.1,and 2.7 kJ·mol-1respectively,and those of using G3MP2 model are 2.3,2.4,4.3,and 3.5 kJ·mol-1respectively.13The average absolute error of Eq.(19)is only 2.6 kJ·mol-1.That is to say,the value of ΔfH0calc.with Eq.(19)is as accurate as that from G3 and G3MP2 model chemistries.Moreover,Eq.(19)avoids bothersome calculations.
3.3 Predicting the ΔfH0of esters
The 27 experimental values of ΔfH0(g)of esters R1C(O)OR2 were taken as a data set to correlate with parameters ΣNC(Ri),ΣΔPEI(Ri),PEI(R1),PEI(R2), ΠPEI(Ri),and ΠΔTSEI(Ri)(see Table 4 and Table 5),and Eq.(20)was obtained.
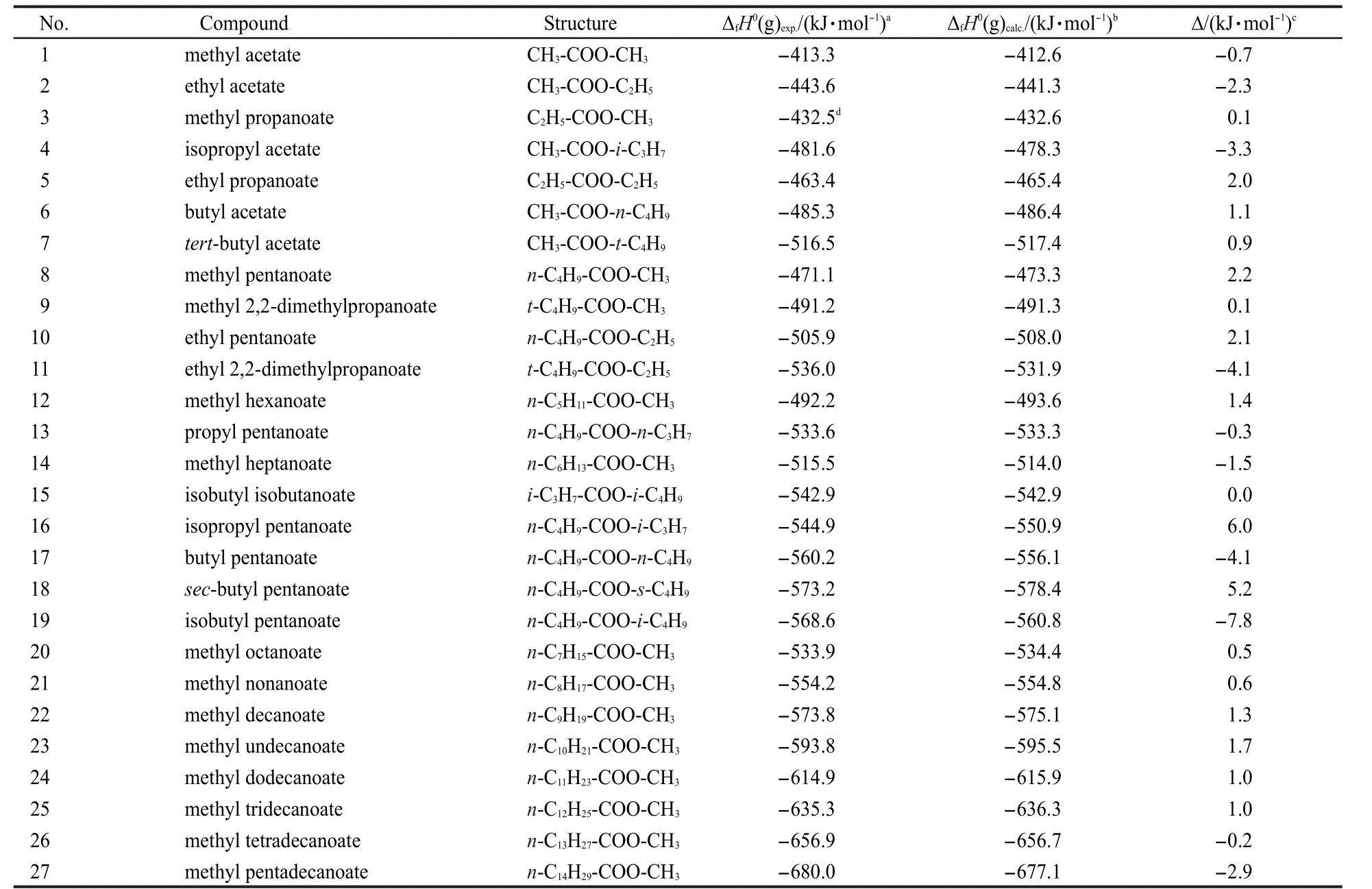
Table 4 ΔfH0(g)values of R1C(O)OR2
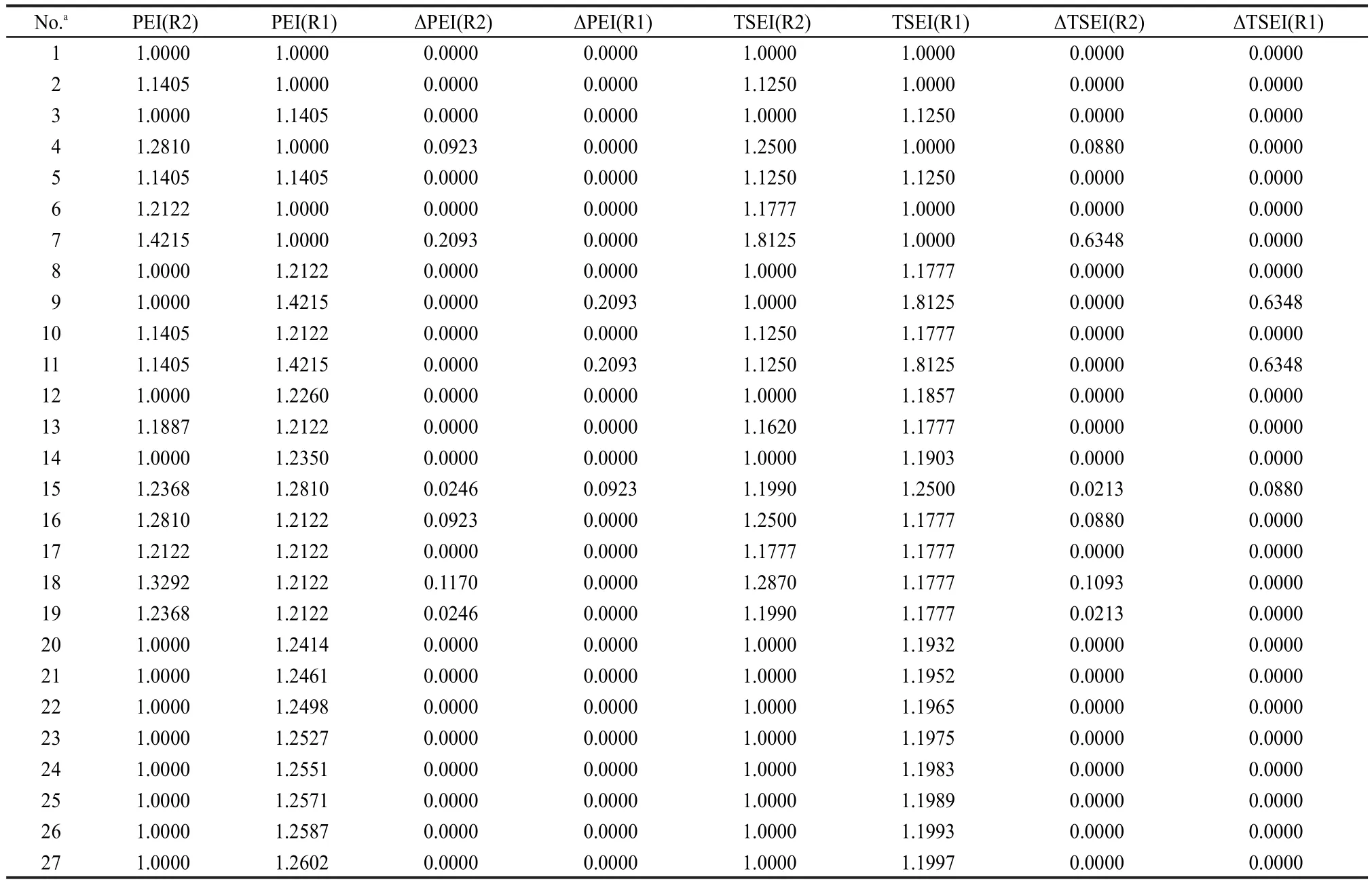
Table 5 PEI,TSEI,ΔPEI,and ΔTSEI values of R1 and R2 in R1C(O)OR2


Fig.2 Plot of ΔfH0(g)calc.calculated with Eq.(20)vs ΔfH0(g)exp.
In Eq.(20),there is a good linear correlation(see Fig.2).The average absolute error between the experimental values and the calculated values is only 2.0 kJ·mol-1,which is less than that of 4.8 kJ·mol-1(G3 model)and 2.4 kJ·mol-1(G3MP2 model),respectively.13The coefficient in front of ΣNC,-20.3905,indicates the contribution of each CH2unit to the ΔfH0(g),which is also closed to that value,-20.69,reported in literature.24This result proved that Eq.(20)can be used to estimate ΔfH0(g)of esters.In this work,the Eq.(20)is employed to predict the ΔfH0(g)of over 200 esters,and these predicted values are also given in the Supporting Information.
4 Conclusions
The intramolecular interactions of the R1-Y-R2 among substituent Y,alkyl R1 and alkyl R2,can be expressed by three parts, φ[R2]φ[R1Y], φ[R1]φ[YR2],and ψ[R1]ψ[R2],with which an extended expression Eq.(2)is derived to express the ΔfH0of R1-Y-R2.The correlation expressions(19)and(20)indicate that this method is rational and effective.The ΔfH0(g)values calculated by Eqs.(19,20)have the same accuracy as those computed by G3 and G3MP2 model chemistries for the compunds thioether,secondary amines,ethers,ketones,and esters.Furthermore,the method of this work can avoid a mass of bothersome calculations for searching an appropriate model,and its parameters are easily obtained.The results also proved that the interaction potential index IPI(X)derived from monosubstituted straight-chain alkanes RX can be used well in the estimation of the enthalpies of formation for R1-Y-R2.
Supporting Information: With Eqs.(19,20),the ΔfH0(g)of 800 two-direction extending compounds were predicted and listed.This information is available free of charge via the internet at http://www.whxb.pku.edu.cn.
(1)Wiberg,K.B.;Waldron,R.F.J.Am.Chem.Soc.1991,113,7697.doi:10.1021/ja00020a036
(2) Laurencelle,N.;Pacey,P.D.J.Am.Chem.Soc.1993,115,625.doi:10.1021/ja00055a035
(3) Milburn,R.K.;Rodriquez,C.F.;Hopkinson,A.C.J.Phys.Chem.B 1997,101,1837.doi:10.1021/jp962303e
(4)Herndon,W.C.;Biedermann,P.U.;Agranat,I.J.Org.Chem.1998,63,7445.doi:10.1021/jo981280s
(5)Zheng,K.C.;Kuang,D.B.;Yun,F.C.;He,F.Acta Phys.-Chim.Sin.2000,16,133.[郑康成,匡代彬,云逢存,何 峰.物理化学学报,2000,16,133.]doi:10.3866/PKU.WHXB20000208
(6)Zheng,K.C.;Zhang,Z.Q.;Shen,Y.;Yun,F.C.Acta Phys.-Chim.Sin.2001,17,448.[郑康成,张仲钦,沈 勇,云逢存.物理化学学报,2001,17,448.]doi:10.3866/PKU.WHXB20010514
(7) Sorkhabi,O.;Qi,F.;Rizvi,A.H.;Suits,A.G.J.Am.Chem.Soc.2001,123,671.doi:10.1021/ja0017312
(8)Yang,F.;Wang,Z.;Huang,Y.;Ding,X.J.Chem.Inf.Comput.Sci.2003,43,753.doi:10.1021/ci025663+
(9)Yang,F.;Wang,Z.;Huang,Y.;Zhou,P.J.Chem.Inf.Comput.Sci.2003,43,1337.doi:10.1021/ci0340512
(10) Exner,O.;Böhm,S.J.Comput.Chem.2004,25,1979.doi:10.1002/jcc.v25:16
(11)Emel'yanenko,V.N.;Kabo,G.J.;Verevkin,S.P.J.Chem.Eng.Data 2006,51,79.doi:10.1021/je050230z
(12) Cao,C.Z.;Liu,J.L.Acta Phys.-Chim.Sin.2007,23,955.[曹晨忠,刘金玲.物理化学学报,2007,23,955.]doi:10.3866/PKU.WHXB20070632
(13) Bond,D.J.Org.Chem.2007,72,7313.doi:10.1021/jo071213a
(14)Thalladi,V.R.;Weiss,H.C.;Blalser,D.;Boese,R.;Nangia,A.;Desiraju,G.R.J.Am.Chem.Soc.1998,120,8702.doi:10.1021/ja981198e
(15) Glaser,R.J.Org.Chem.2001,66,771.doi:10.1021/jo001241s
(16)Ju,X.H.;Li,Y.M.;Xiao,H.M.J.Phys.Chem.A 2005,109,934.doi:10.1021/jp045071p
(17)Gung,B.W.;Zou,Y.;Xu,Z.;Amicangelo,J.C.;Irwin,D.G.;Ma,S.;Zhou,H.C.J.Org.Chem.2008,73,689.doi:10.1021/jo702170j
(18) Mathieu,D.J.Chem.Theory Comput.2012,8,1295.doi:10.1021/ct2006083
(19) Jabloński,M.J.Phys.Chem.A 2012,116,3753.doi:10.1021/jp300993b
(20) (a)Istomin,B.I.;Palm,V.A.Reakts.Sposobnost Organ.Soedin.(Tartu)1971,8,845.(b)Istomin,B.I.;Palm,V.A.Reakts.Sposobnost Organ.Soedin.(Tartu)1972,9,433.(c)Istomin,B.I.;Palm,V.A.Reakts.Sposobnost Organ.Soedin.(Tartu)1972,9,469.(d)Istomin,B.I.;Palm,V.A.Reakts.Sposobnost Organ.Soedin.(Tartu)1972,9,847.
(21) Cao,C.Z.;Gao,S.Acta Phys.-Chim.Sin.2005,21,1028.[曹晨忠,高 硕.物理化学学报,2005,21,1028.]doi:10.3866/PKU.WHXB20050917
(22) Cao,C.Z.;Gao,S.;Zeng,R.J.J.Mol.Struct.-Theochem 2005,728,85.doi:10.1016/j.theochem.2005.05.008
(23)Cao,C.Z.QSAR Comb.Sci.2008,27,555.
(24)Wu,Y.X.;Cao,C.Z.;Yuan,H.Chin.J.Chem.Phys.2012,25(2),153.doi:10.1088/1674-0068/25/02/153-160
(25) Cao,C.Z.;Li,Z.L.J.Chem.Inf.Comput.Sci.1998,38,1.doi:10.1021/ci9601729
(26) Cao,C.Z.Substituent Effects in Organic Chemistry;Science Press:Beijing,2003.[曹晨忠.有机化学中的取代基效应.北京:科学出版社,2003.]
(27) Cao,C.Z.;Liu,L.J.Chem.Inf.Comput.Sci.2004,44,678.doi:10.1021/ci034266b
(28)Haynes,W.M.CRC Handbook of Chemistry and Physics,91st ed.;CRC Press:Boca Raton,FL,2010-2011.
(29) Domalski,E.S.;Hearing,E.D.J.Phys.Chem.Ref.Data 1993,22,805.doi:10.1063/1.555927

