平动式啮合电动机优化设计方法
李瑞华
(许昌学院电气信息工程学院,河南许昌 461000)
0 引言
平动式啮合电动机是一种将平动减速器[1-2]与电动机有效集成的新型电动机结构[3-5],具有传动链短,低转速、大转矩特点,在机器人、航空航天驱动系统有着较好的应用前景。目前,现有的几种平动式啮合电动机在结构本身存在磁场耦合、负功磁路、平动惯量大、功率密度低等问题,还需要进一步改进,但已基本确立平动电动机的基本机构和运行特点。此外,当前针对与平动式类电动机的理论研究主要集中在静态特性分析研究[6]、磁路模型分析[7]或控制方法研究[8-9]等方面,而关于优化设计理论方面的研究尚处于空白,使得平动类电动机的结构设计参数缺乏统一的理论指导,不能完全体现出平动式啮合电动机的性能优势。
本文根据平动类电动机的结构特点,借鉴常规电动机优化设计方法,采用等效磁路方法建立了双转子平动电动机的磁路模型。在建立的模型基础上,通过气隙能量与电动机输出能量的关系,推导出了电动机效率与磁极结构参数的关系模型,为平动类电动机设计提供理论指导。
1 磁极结构优化设计与分析
1.1 优化目标分析
电动机的性能指标主要有功率密度、效率、输出转矩、响应速度等,影响这些指标的最关键部分是电动机的磁极结构。磁极的结构形式、尺寸比例、参数选择、材料特性及工艺方案等种种因素都对其性能指标产生不同程度的影响。
根据平动电动机的磁极特点,将文献[5]中如图1(a)所示的磁极结构简化为如图1(b)所示的磁极标准几何模型。模型忽略了定子磁轭部分铁心宽度的变化,并将磁路部分视为等宽度,磁极简化前后在能量转换方式上相同,磁极定、转子的各个部分尺寸参数关系明确,具有代表性并且与实际平动磁极结构形状较为相似,不影响分析的准确性,对于优化设计较为方便。
图1(b)中参数含义:磁极宽度d,最大气隙长度g,绕组尺寸c和e。固定参数为输出功率和磁极整体尺寸a、b及硅钢片叠压厚度h。其他参数的取值,并不影响优化的结果,如绕组线径、材料特性等。

图1 磁极结构简化Fig.1 Simplify structure of magnetic poles
机器人驱动电动机通常有安装空间体积、输出功率的要求,因此本文优化目标是在满足体积和功率的条件下,寻求最佳的磁极结构参数,获得最高的效率。平动电动机效率的计算式为

式中:Pt为电动机输出功率;Pe为输入电功率;Pr为绕组热损耗。
1.2 能量转化原理
平动电动机输出的机械能是由磁场能转化而来的,磁场能是有电能提供的,具体关系为

式中:ΔWe为输入电能变化;ΔWf为输出机械能变化;ΔWm为磁场能的变化;ΔWr为绕组热损耗能量。
磁场能量主要存储在气隙中,磁极的每次吸合释放一次能量,另外,为使电动机性能处于最佳状态,磁极一般都工作在磁饱和状态,磁极铁心内的磁通密度始终可以通过调节绕组电流达到处于饱和状态,忽略损耗和漏磁,输出的机械能将全部由气隙磁场提供。计算气隙磁场的关键是气隙磁导的形状的确定,图2显示了气隙磁场在磁极吸合过程中的形状变化,其中的G1,G2,G3,G4,G5,G6代表 6 部分的气隙磁导,Os为转子的公转中心点,Or和O'r分别代表转子启动时和吸合后的位置,δ为气隙长度变量,d1与d2分别为两个处气隙的极对面长度。从图1、2中可以看出,存在d1=d。
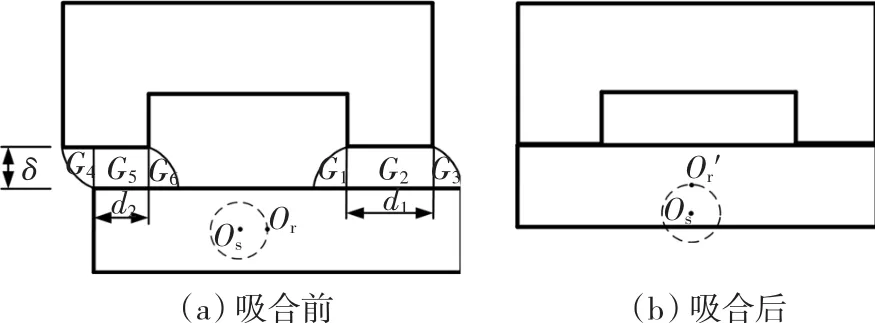
图2 气隙变化Fig.2 Air gap change
根据图2,忽略漏磁,假设为恒磁通控制,磁极吸合前后的气隙磁场能变化为
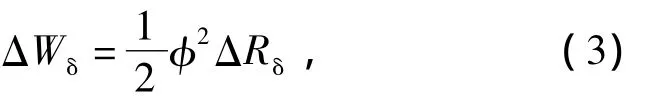
式中:ΔWδ为气隙磁场能变化;ΔRδ为气隙磁阻变化;φ为磁通量。
气隙磁导G1~G6可采用磁通管方法确定[10],即

式中:μ0为气隙磁导率,μ0=4π ×10-7A/m;θr为转子公转角。
气隙磁导G1、G2、G3之间是并联,同样地,G4、G5、G6也是并联,而G1、G2、G3和G4、G5、G6之间是串联形式,因此总的气隙磁阻为

再将式(4)代入,则总的气隙磁阻Rδ为

磁路中的磁动势与磁压降的关系为

式中:Hi为铁心磁场强度;Hδ为气隙磁场强度;li为铁心磁路平均长度;N为绕组匝数;I为电流。
忽略气隙轴向漏磁,根据磁通连续性特点,气隙磁压降可由磁通量和气隙磁阻表示,并考虑铁心磁通量与磁通密度、结构尺寸关系,可将式(7)改写为
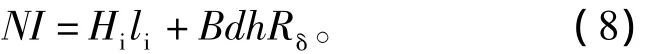
设Wr为绕组热损耗,单位时间段Δt内的热损耗 ΔWr为

式中,Rw为绕组电阻。
设lw为线圈长度,ρ为铜电阻率,则Rw的计算式为

式中,dr为绕组线径。
绕组允许通过的最大电流Imax与导线直径dr,工作频率,散热能力有关。
1.3 优化约束条件分析
1.3.1 几何条件
在电动机体积已知和啮合及约束机构占用空间确定情况下,磁极所占用的体积是确定的,即a、b、h为定值,由图1(b)中的几何关系可以得到

式中:Sw为绕组横截面积;Kw为填充系数。
1.3.2 温度条件
电动机绕组的散热能力与多个方面相关,如电动机工作环境温度,通风条件、缠绕方式等,较难采用一个具体方程式计算,绕组所能承受的最大温升值还需要试验确定,因此在本文的优化计算中将不做具体计算。
1.3.3 功率约束条件
在最大气隙位置时,气隙磁场所能存储的最大能量决定了电动机输出能量的上限。由最大输出功率Pg,转速ωo及工作方式可以得到磁极能量条件。一个磁极气息磁场能量与瞬时输出功率的关系为

式中:Wg为输出能量,单位W;ωo为输出转速,单位r/min;iz为减速比;ε为转子公转一周磁极吸合节拍数。
假设控制器能够调整电流使一个磁极的铁心磁通密度B始终处于饱和,则输出能量完全由气隙能量提供。根据式(3)、式(12)可得到磁极的磁通密度与瞬时输出功率关系为

在转子工作的1/4公转周期内,由于转子与齿圈固联,气隙变化与转子平动公转半径r相等,即δ=r。
1.3.4 优化函数
将式(6)、式(7)代入式(1),得

式中,Ip为Δt时间内的平均电流,有Ip=I/2。可根据式(8)得平均电流表达式为

将式(6)、式(11)代入式(14)可以得到效率优化函数为

2 算例优化分析
假设要设计的电动机的安装体积和输出功率及输出转速已知,优化目标是效率达到最大。设定输出功率Pt=200 W,转速ωo=230 r/min,传动比iz为13;上电工作方式为4拍方式,根据传动比和输出转速可以求得磁极的吸合时间为0.005 s。在此过程中释放能量可由式(12)计算得Wg=0.99 J;铁心材料为DW54 0-50。其他参数设置为:绕组线径dr=0.9 mm,电阻率 ρ=1.75×10-8Ωm;磁极高a=29.5 mm;磁极宽b=29.5 mm;气隙磁导率 μ0=4π×10-7H/m;铁心厚度h=28 mm;饱和磁通密度Bmax=1.85 T;饱和磁场强度Hmax=14 006 A/m。考虑实际电动机结构中的机械结构强度问题,设定铁心宽度d的变化为3~7 mm,将上述参数代入式(16)、式(15)可以得到效率随铁心宽度的变化曲线,如图3所示。

图3 效率变化曲线Fig.3 Efficiency curve at different core width
同样,再将d代入式(13)可以得到气隙长度g的变化曲线,如图4所示。实际上,图4中的气隙变化曲线以上部分范围内的取值都可以满足式(13)的能量条件。

图4 气隙长度变化曲线Fig.4 Air gap curve at different core width
利用几何条件式(11)求得满足能量条件时的匝数N随d和g的变化曲线,如图5所示。
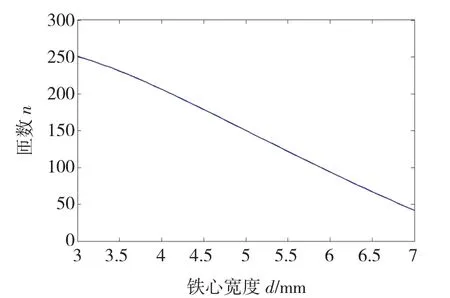
图5 匝数变化曲线Fig.5 Turns curve at different core widths
在确定了结构参数后,还需要计算最大气隙处磁场储能达到Wg时所需要的励磁电流,图6为根据式(8)获得的励磁电流随铁心宽度变化曲线。

图6 励磁电流变化曲线Fig.6 Excitation current curve at different core width
取图3中最大效率点74%时的铁心宽度值d=5 mm,最大气隙长度g=1.4 mm,则最大励磁电流I=37 A。此时的磁链Ψ和电感L的计算式为

绕组的工作时间为0.005 s,需要计算能够满足最大励磁电流和工作时间要求的绕组驱动电压。假设在气隙磁场储能为达到最大之前磁极未发生移动情况,绕组驱动电压的计算式为
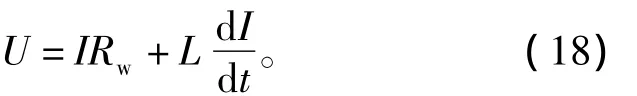
如图7所示,在驱动电压在30 V时,匝数取150匝时,电流可以在0.003 s内上升至37 A,说明所计算的磁场结构参数能够满足电流上升时间要求。

图7 电流随时间变化曲线Fig.7 Current curve versus time
3 物理样机性能
图8是为一种双转子平动式啮合电动机样机,该电动机的每个磁极形状采用了一种图8(b)所示的双转子式结构,两个转子相向运动可以抵消惯性力并增大转矩,零件制造材料为硬铝合金与普通碳钢。电机的磁极结构参数取值采用2节中的优化计算结果:定子中部宽度10 mm、转子宽度5 mm,气隙长度1.4 mm,匝数150。

图8 新型平动式啮合电动机结构Fig.8 Structure of novel translational meshing motor
通过磁粉制动器、扭矩传感器和电参数采集仪构成的实验平台可以获得样机效率随转速变化曲线,如图9所示。

图9 效率随转速变化曲线Fig.9 Efficiency curve at different velocity
在算例分析中,优化设计目标是要在输出转速为230 r/min时能够达到最大效率,优化计算结果得到了该转速时的最大效率为74%,而图9中的电动机效率在转速在230 r/min时的最大效率值为58%,这比优化计算结果要小16%,这是由于优化计算仅仅考虑的是磁极部分的优化,而没有考虑啮合传动效率损失和平动约束机构的摩擦及加工误差造成的损耗,这一部分的损耗使得样机试验结果要小于优化结果。
表1是几种现有平动式啮合电动机的性能比较结果,其中前三种平动电机的设计功率、输出转矩相差较大,这是由于前两种电机在设计时并未考虑参数的优化问题,仅考虑了机构原理的实现,没有统一设计参数。柔性平动式啮合电机II的性能参数是对I电机的定子宽度、匝数、气隙长度参数优化而不改变其他结构的情况下得到的实验结果,可以看出电机的效率提升了15.4%,其他性能参数也有相应提升,但提升有限,这是由于该电机采用了柔性铰链约束机构,无法完全约束转子的公转半径,造成了滑齿现象,限制其功率与效率的提升。双转子平动电机性能参数是在改进前两代电机机构设计缺陷的基础上,同时优化电机磁极结构参数后得到的实验结果,该电机在转矩质量比和功率密度上有较大提升,这是由于效率优化算法相当于是在体积限定的情况下使输出转矩最大的优化方法,从而获得了较高的转矩质量比,达到了前两代电机的15~20倍。

表1 性能比较Table 1 Performance comparison
4 结论
本文根据当前已有的几种平动式啮合电动机磁极结构特点,采用磁路方法建立了磁极的磁路模型,得到了磁极能量转化效率与磁极结构参数的关系,推导出了基于效率最优的平动式啮合电动机结构参数计算公式,并得到了以下结论:
1)基于能量原理的平动电动机优化方法计算模型与平动电动机磁极的实际结构特点较为接近,计算过程简单,可变参数少。
2)几种已有的平动电机的样机试验结果证明了经参数优化后的平动电动机在转矩重量比、功率密度和效率都有较大提升,说明了优化方法的有效性。
3)物理样机试验得到的效率结果较理论计算低,这是由于优化方法并未考虑齿轮啮合的效率和平动约束机构及加工误差、摩擦等造成的损耗,这部分的优化计算方法可借鉴类似机构的一些效率分析方法作。
平动电动机结构较为特殊,磁极形状较常规电动机差别较大,试验数据的积累较少,本文提出的优化方法是在磁极体积、功率和转速为约束条件时的效率优化算法,在转矩、功率及温升等方面的优化尚未做深入讨论,这方面的研究将作为下一步的研究目标,进而逐步完善平动式啮合电动机设计理论。
[1]赵自强,张春林,程爱明,等.内平动齿轮传动齿廓重叠干涉限制条件研究[J].北京理工大学学报,2008,28(10):856-859.
ZHAO Ziqiang,ZHANG Chunlin,CHENG Aiming,et al.Profile overlap interference constraint conditions of internal parallel move gears transmission[J].Transactions of Beijing Institute of Technology,2008,28(10):856-859.
[2]赵自强,张春林,程爱明.分流型内平动齿轮传动原理及实现[J].水利电力机械,2007,29(9):22-25.
ZHAO Ziqiang,ZHANG Chunlin,CHENG Aiming.Element sand realization of internal parallel move gears transmission of power diffluence[J].Water Conservancy & Electric Power Machinery,2007,29(9):22-25.
[3]XU Qiang,LIAO Qizheng,WEI Shimin,et al.Construction principle and torque solution of the translational meshing motor[C]//IEEE International Conference on Mechatronics and Automation,August 5-7,2007,Harbin,China.2007:2894-2899.
[4]徐强,廖启征,魏世民,等.柔性平动式啮合电动机结构原理及静态转矩[J].中国机械工程,2009,20(3):288-292.
XU Qiang,LIAO Qizheng,WEI Shimin,et al.Construction principle and static torque of translational meshing motor integrated with compliant mechanism[J].China Mechanical Engineering,2009,20(3):288-292.
[5]李瑞华,廖启征,魏世民,等.径向驱动式啮合电动机设计与静态转矩分析[J].高技术通讯,2011,21(3):297-302.
LI Ruihua,WEI Shimin,LIAO Qizheng,et al.Design and static torque analysis of a radial driving meshing motor[J].Chinese High Technology Letters,2011,21(3):297 -302.
[6]徐强,廖启征,魏世民,等.基于等效磁路法的平动式啮合电动机静态转矩求解[J].北京化工大学学报,2008,35(2):76-81.
XU Qiang,LIAO Qizheng,WEI Shimin,et al,An improved magnetic equivalent circuit method for predicting static torque of a translational meshing motor[J].Journal of Beijing University of Chemical Technology,2008,35(2):76-81.
[7]徐强,廖启征,魏世民,等.平动式啮合电机的非线性等效磁路模型[J].电机与控制学报,2008,12(2):126 -131.
XU Qiang,LIAO Qizheng,WEI Shimin,et al.Nonlinear model of translational meshing motor based on magnetic equivalent circuit method[J].Electric Machines and Control,2008,12(2):126 -131.
[8]李瑞华,魏世民,廖启征,等.柔性平动式啮合电机动态分析与转矩控制[J].电机与控制学报,2009,13(3):408-413.
LI Ruihua,WEI Shimin,LIAO Qizheng,et al.Dynamic analysis and torque control of translational meshing motor integrated with compliant mechanism[J].Electric Machines and Control,2009,13(3):408-413.
[9]李瑞华,廖启征,魏世民,等.径向驱动式啮合电机建模与仿真研究[J].电机与控制学报,2010,14(4):14 -19.
LI Ruihua,WEI Shimin,LIAO Qizheng,et al.Modeling and control study for radial driving meshing motor[J].Electric Machines and Control,2010,14(4):14 -19.
[10]孙雨施,王素菊,曲民兴,等.直流磁系统的计算与分析[M].北京:国防工业出版社,1987:55-57.

