电网电力系统稳定器的交互影响分析

康礼彦 王克文 王君亮

(郑州大学电气工程学院1，河南 郑州 450001;河南电力试验研究院2，河南 郑州 450052)

0 引言

近年来，随着电网规模的扩大和机电振荡模式的增多，多机系统机组间的交互影响逐渐明显。机组上所安装的电力系统稳定器(power system stabilizer，PSS)在提高机电振荡模式阻尼比的同时，可能会对机电振荡模式产生不利影响。

基于系统单运行方式，PSS最佳安装位置可根据传统的参与因子法[1－4]、基于 Prony 分析的留数法[5－7]和特征值灵敏度分析法[8－11]来确定，其中概率特征值灵敏度分析法[12－15]为多运行方式下的系统稳定性分析提供了可靠的选择指标。文献[3－4]采用参与因子法及模态分析选取PSS合适的安装位置。文献[11]采用特征分析法确定多机系统中PSS的最佳安装位置。

对10个机组以下的小系统，根据特征值灵敏度可以很容易地确定各机电模式的主参与机组或强参与发电机。而在省级电网中，由于多机系统机组间的交互影响，人工确定对应各模式的PSS安装位置比较困难。因此，本文采用特征值灵敏度分析法建立优化模型，以分析系统中PSS的交互影响。

1 特征值分析法

基于多机系统表达式(generalized multimachine representation，GMR)及插入式建模技术(plug-in modeling technique，PMT)的电力系统仅由两类基本传输块构成。用于形成系统A的微分-代数方程[10]可简单表示为:

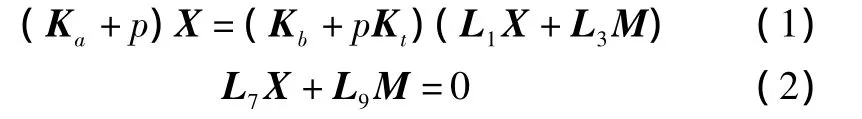
式中:X和M分别为状态变量和非状态变量矩阵;Ka、Kb和Kt分别为一阶传输块参数的对角矩阵;L1和L3为子矩阵，仅由0和1构成;L7和L9则描述了状态变量和非状态变量的代数关系。

将导纳矩阵Y的网络方程式ΔI=YΔV插入到L9中，得到4个实数矩阵，并消去式(1)和式(2)中的非状态变量M，即可得到以下矩阵:

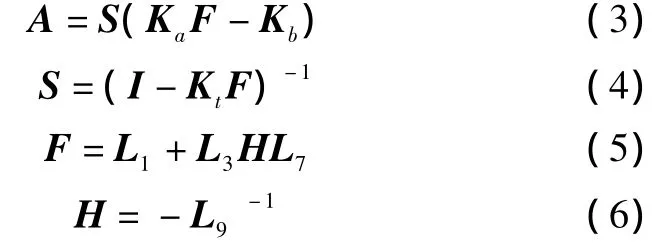
式中:F和H为特征值计算中的中间矩阵。

用于电力系统小干扰稳定分析的特征值由A阵求得。QR算法[16]是求取全维特征值的有效算法之一，具有数值稳定、收敛可靠的优势，但存在维数限制问题。近年来出现的改进后QR算法可有效求解几千阶规模的矩阵。本文用QR算法求系统的特征值。

2 特征值灵敏度

特征值灵敏度既可用于确定机电振荡模式，又可用来选择PSS的最佳安装位置，其数值大小反映了单位增益变化引起的特征值变化程度，正负号体现了特征值的变化趋势。

设Wk和Uk分别为第k个特征值λk的左、右特征向量，且已经标准化，即WTkUk=1，则第k个特征值λk=αk±jβk对第 m 个 PSS增益 Km的灵敏度[8]可表达为:

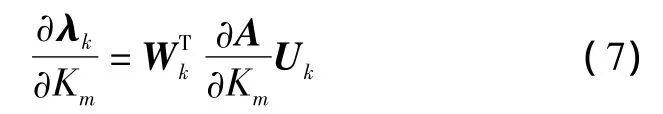
由式(7)可知，系数矩阵A对PSS增益Km的导数对求解特征值的灵敏度具有重要的作用，则:

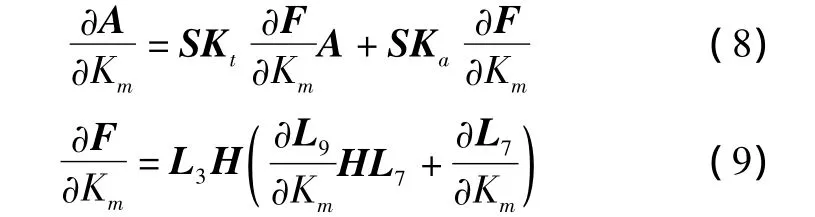
本文仅关心特征值实部αk及阻尼比ξk对PSS增益Km的灵敏度。由于:

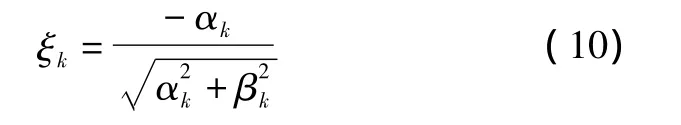
因此有:

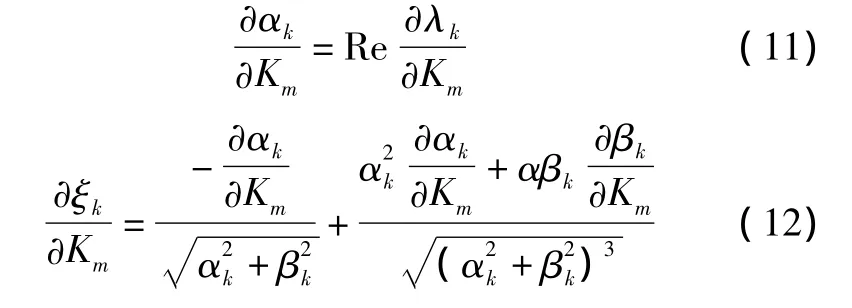
3 PSS交互影响分析

电力系统各机组间容易出现交互影响。某8机系统部分机电模式的特征值灵敏度如表1所示。其中，K表示各PSS对应的增益;α表示各机电振荡模式。

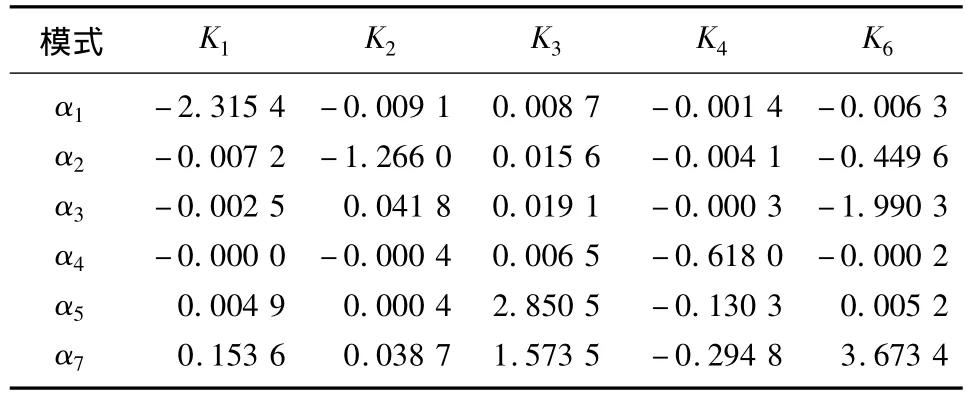
表1 特征值对PSS增益的灵敏度Tab.1 Sensitivities of engenvalues to gains of PSS

发电机上安装了PSS，K值表示相应机组的增益。由表1可见，模式 1、2、4和机组 1、2、4 只有一个灵敏度值很大，且一一对应，因此模式1、2、4的主参与机组分别为机组1、2、4;而机组3和机组6均控制两个模式，且模式7由机组3和机组6同时控制，因此存在交互影响。模式5和模式7的灵敏度方向相同，可以在发电机3上安装PSS同时改善两个模式;而模式3和模式7灵敏度方向相反，在发电机6上安装PSS可能会对两个模式起到相反的作用，于是有必要对此情况做优化处理。

由上述分析可知，当灵敏度方向相同时，在某机组上加装PSS，可以同时改善多个机电振荡模式的阻尼特性。因此，本文只考虑有交互影响且灵敏度方向相反的机组。

构成的目标函数可表示为:

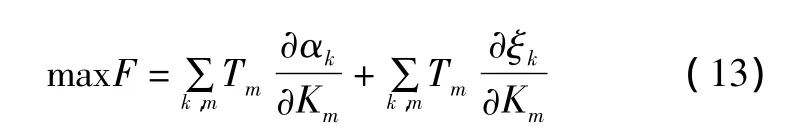
式中:Tm为第m台发电机的权重系数，反映每台发电机PSS的参与情况。当m=0时，表示发电机上不安装PSS;当m=1时，表示安装PSS;当m=－1时，则表示安装PSS但符号相反。Tm的值由枚举产生。

式(13)中仅包含了PSS有交互影响且作用相反的机组及其相关的机电振荡模式。机电模式的灵敏度有正有负，可能增强或削弱模式的阻尼。Tm的使用正是为了协调这种影响。

为了分析PSS的交互影响，得到各机电振荡模式的主参与机组，每个机电振荡模式应尽可能选择最灵敏的机组。当机电振荡模式对某台发电机PSS的灵敏度影响很小时，在这台发电机上安装PSS对机电模式的改善效果并不明显，因此，可以通过设定门槛值来选择需要优化的相关机组，并形成新的模块进行求解。方法实现的过程如下。

①建立状态空间方程，形成系数矩阵A。根据式(3)～式(6)，采用QR算法，求出特征值λ。

②由步骤①得到矩阵A和左右特征向量W、U，根据式(7)～式(12)，求解零增益下特征值实部α的灵敏度及阻尼比ξ的灵敏度。

③根据特征值的灵敏度大小，选出每个机电模式的主参与机组，并判断各机组主导的机电模式的个数N。若N＞1，且对应的机电模式的灵敏度方向相反，则进行优化处理;否则，保存这些机组的主导模式。

④搜索需要优化处理的机组所主导的机电振荡模式，并根据设定的门槛值，选择各模式的相关机组，以做进一步的优化。

⑤将选出的满足优化条件的机组及其主导的各机电模式形成新模块。根据式(13)和式(14)，采用枚举法进行优化处理，得到各机电振荡模式的主参与机组并予以保存。

⑥根据最终得到的各机电模式的主参与机组，用PSS控制其主参与模式，并进一步做PSS参数的协调优化，判断该方法的有效性。

4 算例分析

4.1 特征值计算

算例采用2011年冬季大运行方式的运行数据。考虑的省网共有1 124个节点、1 103条线路、180台双绕组变压器、445台三绕组变压器。

运行发电机数为109台，其中某电厂内两台发电机的机组参数、控制器参数完全一致，将其合并为一台，加上4台边界等值机。特征值计算中，共考虑112台发电机，存在111种机电振荡模式。用QR法计算全维特征值和左、右特征向量矩阵W和U，得到1 623个特征值。用右特征方程校核，误差中实部和虚部的最大偏差值为 －3.610 54×10－8;左特征方程校核的最大误差为1.617 38×10－8;左、右特征向量乘积的最大误差为 －1.209 25 ×10－11。

4.2 零增益下交互影响分析

在零增益下，计算特征值实部灵敏度和阻尼比灵敏度。由于同一个振荡模式的两类灵敏度的值基本对应，根据特征值实部灵敏度选择每个模式下最灵敏的机组，即各模式的主参与机组，共得到18组具有交互影响的机组。

当同一机组主导的不同机电模式的灵敏度方向相同时，通过调整一台发电机上的PSS参数，可以同时改善其他的机电振荡模式;而当灵敏度方向相反时，则会消弱其他机电模式的阻尼。机组50768相关的机电模式灵敏度如表2所示，其中 G50711、G50712、G50719表示与机组50768有交互影响的机组。

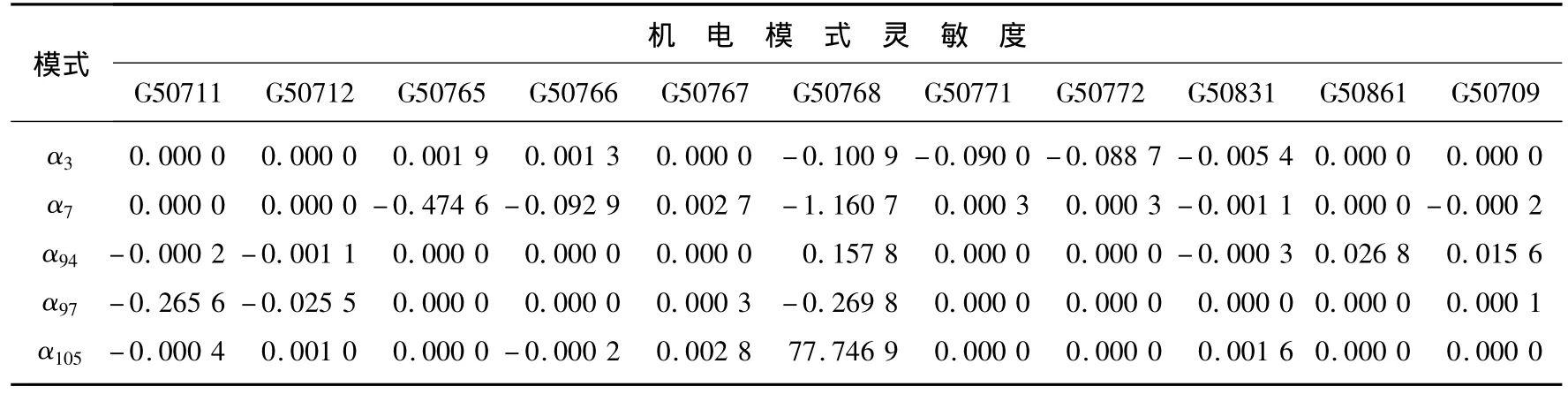
表2 机组50768相关的机电模式灵敏度Tab.2 Sensitivities of electromechanical modes related to unit 50768

以上5种模式的主参与机组均为50768，但其灵敏度方向不一致，需要做进一步优化处理。此处设定灵敏度的门槛值为0.002，针对各机电模式选择相关机组，即共有11台相关机组，由此形成新模块。根据优化模型，通过枚举法确定各机组权重系数的值，从而得到各机组PSS的参与情况。

本算例中，由机组 50768、50845、50846和 50868主导的机电振荡模式灵敏度方向不完全一致，即共有4组交互影响的机组需要做进一步的优化处理。

通过枚举法求解优化模型。将这4组发电机模块分别经过PSS的交互影响分析，最终与同一机组主导的机电振荡模式灵敏度方向保持一致，且数值都相对灵敏，从而使得总灵敏度之和最大，即选定了PSS的最佳安装位置。交互影响分析前后的主参与机组的部分结果如表3所示。

表4给出了各模块的计算规模，其中机组50768的模块计算维数较大，但由于模块规模很小，计算速度很快;其他模块，由于维数很小，计算时间更短，甚至接近0。

各机电模式由其主参与机组的PSS控制，并经过PSS参数的协调优化。优化后的机电模式如表5所示。

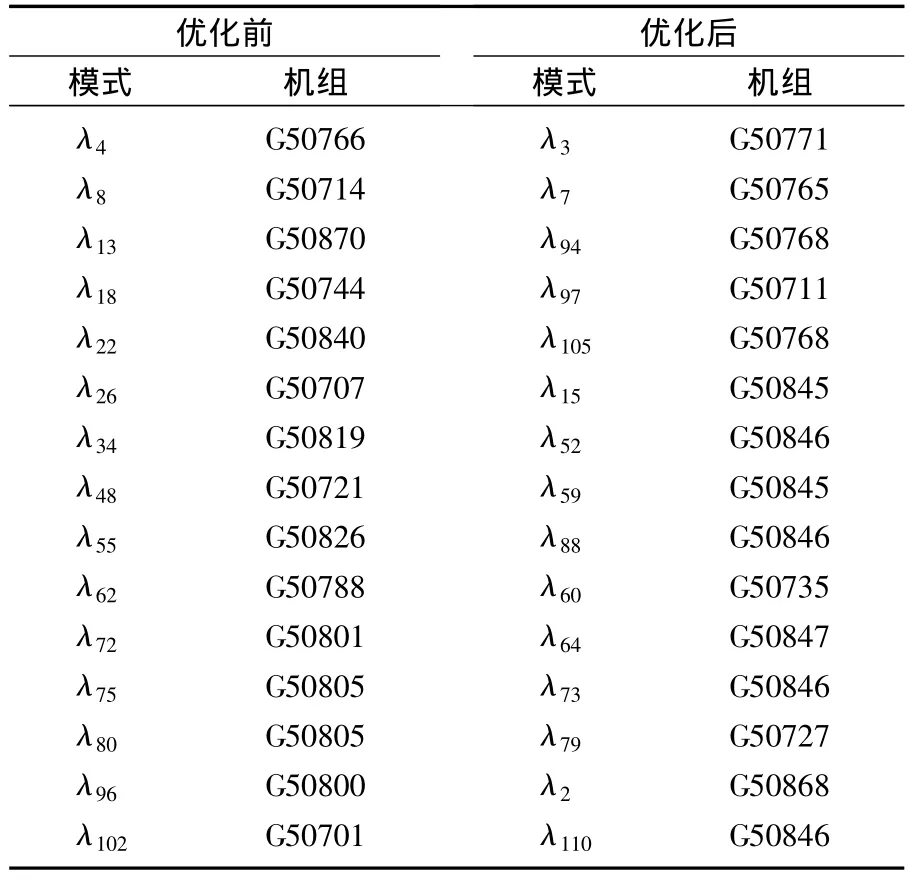
表3 各机电模式的主参与机组Tab.3 The mainly participating generation unit of each electromechanical mode

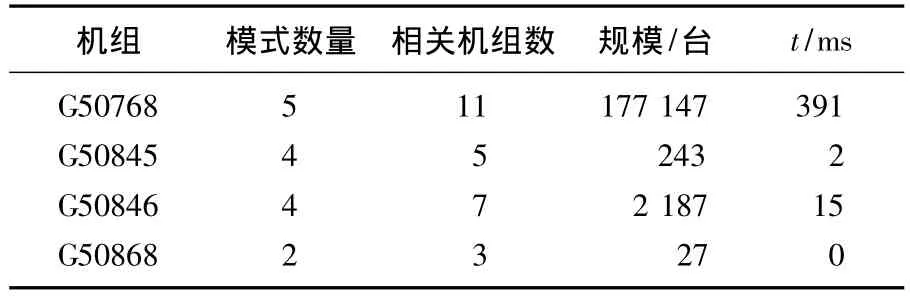
表4 计算规模Tab.4 Calculating scale

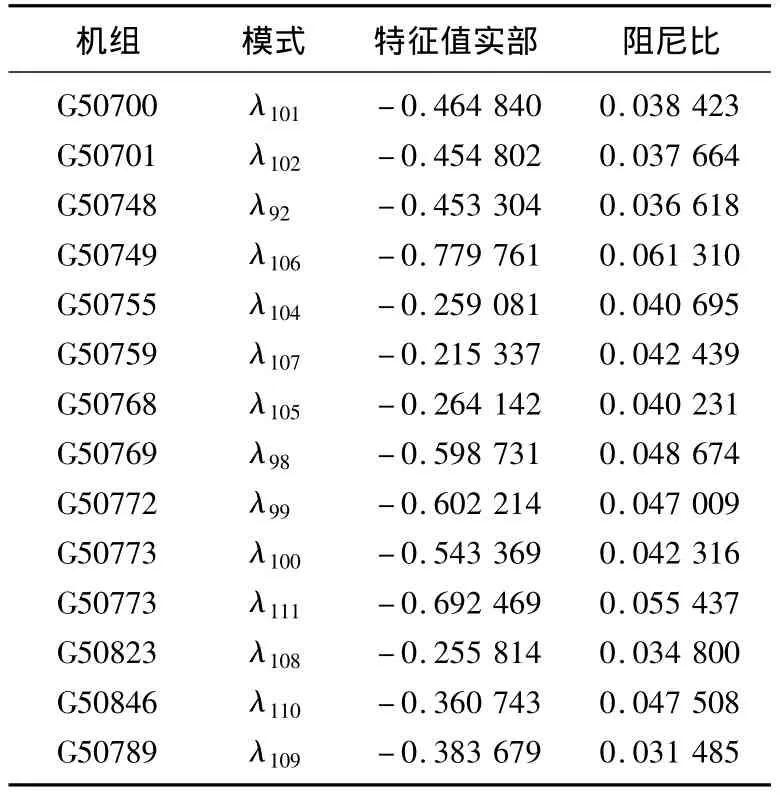
表5 优化后的机电模式Tab.5 Electromechanical modes after optimization

本文将机电模式满足优化的条件定为特征值实部大于－0.03或阻尼比小于0.05，而优化后稳定的条件为特征值实部小于－0.01且阻尼比大于0.03。表5中只列出了需要PSS优化的机电振荡模式。由表5可知，优化后每个机电模式都得到了改善，特征值实部均小于－0.2，阻尼比均大于0.03，满足了机电模式的稳定条件。

5 结束语

本文根据特征值灵敏度的大小对机电模式的主参与机组进行初步选定，并通过判断交互作用机组的特征值灵敏度方向，对灵敏度方向相反的机组做进一步的优化分析，选择相关机组建立新模块，用枚举法求解优化模型，得到机电模式与主参与机组PSS的最佳对应关系。对某省级算例的PSS交互影响分析及参数协调优化的结果表明，采用特征值灵敏度分析法来分析机组PSS的交互影响，可以得到满意的效果。

[1] Kunder P.Power system control and stability[M].New York:Mc Graw-Hill Professional，1994.

[2] 杨晓静，赵书强，马燕峰.采用广域测量信号的PSS参数优化设计[J].电力自动化设备，2006，26(3):47 －50.

[3] 徐光虎，苏寅生，孙衢，等.基于特征值分析法的PSS最佳安装地点的确定[J].继电器，2004，32(8):1 －4.

[4] 韩肖清，梁睿灵，韩肖宁.基于PSASP的PSS选址及参数整定的仿真研究[J].电力学报，2007，22(4):432 －435.

[5] 芦晶晶，郭剑，田芳，等.基于Prony方法的电力系统振荡模式分析及PSS参数设计[J].电网技术，2004，28(15):31－34.

[6] 管秀鹏，程林，孙元章，等.基于Prony方法的大型互联电网PSS参数优化设计[J].电力系统自动化，2006，30(12):7 －11.

[7] 郭成，李群湛，王德林.基于Prony和改进PSO算法的多机PSS参数优化[J].电力自动化设备，2009，29(3):16 －21.

[8] Tse C T，Tso S K.Design optimization of power system stabilisers based on modal and eigenvalue sensitivity analyses[J].IEEE Pro-C，1988，135(5):406 －415.

[9] Voumas C D，Papadias B C.Power system stabilization via parameters optimization-application to the hellenic interconnected system[J].IEEE Transactions on Power Systems，1987，2(3):615 －622.

[10] Wang K W，Chung C Y，Tse C T，et al.Multimachine eigenvalue sensitivities of power system parameter[J].IEEE Transactions on Power Systems，2000，15(2):741 －747.

[11] 翁祖泽.用特征分析法决定多机系统中稳定器的最佳安装地点[J].电机工程学报，1982(4):22－31.

[12] Chung C Y，Wang K W，Tse C T，et al.Probabilistic eigenvalue sensitivity analysis and PSS design in multimachine systems[J].IEEE Transactions on Power Systems，2003，18(4):1439 －1445.

[13] Chung C Y，Wang K W，Tse C T，et al.Power system stabilizer(PSS)design by probabilistic sensitivity indexes(PSIs)[J].IEEE Transactions on Power Systems，2002，17(3):688 －693.

[14] Tse C T，Wang K W，Chung C Y，et al.Parameter optimization of robust power system stabilisers by probabilistic approach[J].IEEE Proceedings of Generation Transmer and Distribution，2000，147(2):69 －75.

[15] 邱磊，王克文，李奎奎，等.多频段PSS结构设计和参数协调[J].电力系统保护与控制，2011，39(5):102 －107.

[16] 王锡凡，方万良，杜正春.现代电力系统分析[M].北京:科学出版社，2003.