遗传算法在某固体火箭发动机中的应用*

张阳新，王敏毅，齐子凤

（中船重工第710研究所，湖北宜昌 443003）

0 引言

固体火箭发动机优化设计是一个多变量，有约束的非线性规划问题，数学描述为:设计变量 X=，目标函数f（X）最大或最小，且满足某些约束条件。工程实际应用中，发动机在完成初步设计后，一般采用如罚函数、复合变形法等传统优化计算方法对其进行优化，此类方法比较经典、灵活，但对于关系复杂、设计变量较多的优化问题，一般收敛速度较慢，且要求目标函数连续可微等，最终结果可能只是局部最优解，近年来，在非线性问题的求解过程中出现了其它优化速度更快、效果更好的智能优化算法。

遗传算法［1－2］是一种智能优化算法，它是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，它将问题的求解表示成“染色体”的适者生存过程，通过“染色体”群的一代代不断进化，包括复制、交叉和变异等操作，最终收敛到“最适应环境”的个体，从而得到问题的最优解。利用遗传算法隐含并行性和强大的全局搜索功能，文中对多根管状装药、锥形直喷管的固体火箭发动机进行了优化设计方法研究。

1 数学模型的建立

1.1 物理模型

研究对象为某小型固体火箭发动机，其结构简图如图1所示。在参数建模时，为简化计算，喷管、燃烧室以及中间底等采用了均壁处理。

图1 发动机结构简图

1.2 目标函数

重量比冲是衡量发动机性能的重要指标，以发动机重量比冲最大为优化准则，对其进行优化设计。发动机重量比冲为:

1.3 设计变量

设计变量应选择对目标函数影响较大，且目标函数有明显极值存在的变量，优化中选取以下6个变量为设计变量:1、燃烧室内径Di;2、平均工作压强¯p;3、喷管扩张半角α;4、喷管喉部直径dt;5、喷管膨胀比εA;6、发动机工作时间t。

1.4 质量模型

1.4.1 药柱质量

在第一轮设计中，发动机装药量基本满足性能要求，为简化发动机优化设计复杂性，药柱质量取原来的装药量不变，且沿用原三根管形装药方案，这样，只需要根据药柱通气参量便可获得药柱内外径以及药柱长度，因此，通气参量便可作为性能约束计算中的变量。

1.4.2 燃烧室壳体质量

燃烧室壳体可视为受内压力作用的薄壁圆筒处理。燃烧室壳体质量为为燃烧室壁厚，其大小必须满足材料最大许可应力要求，即为发动机最大工作压力，计算时取pmax=1.3¯p，D为燃烧室平均直径，Lc为燃烧室壳体长度，由图1可知，Lc等于药柱长度、喷管收敛段长度以及后挡药板厚度三者相加。

1.4.3 喷管质量

喷管采用的是简单锥形直喷管，收敛半角取原始设计值45°，扩张半角设为变量，根据相关参数计算，喷管质量为。式中，f（x）为喷管内型面方程。

1.4.4 其它质量

其它质量为除去壳体和喷管质量以外的所有结构质量，包括前、后挡药板质量、中间底质量以及点火具等。由计算得，前挡药板质量为md1=ρd·Sd1·δd1;后挡药板质量为md2=ρd·Sd2·δd2;中间底质量为点火具质量取定值。式中，δc、δd1、δd2、δz分别为燃烧室壳体、前、后挡药板和中间底厚度，其数值同样必须满足材料强度要求，Lz为中间底长度，ρ为材料密度。

由以上各部分质量叠加得到发动机总质量:

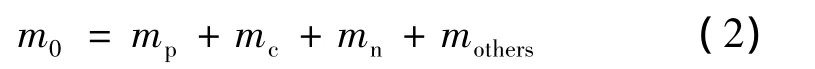
1.5 能量模型

1.6 约束条件

发动机设计中包括有几何约束、性能约束和结构强度约束等。几何约束主要包括发动机总长和发动机直径，发动机总长由喷管、燃烧室和中间底的轴向长度决定，发动机直径需满足弹总体要求，即小于0.55倍的弹身直径;性能约束包括发动机的工作压强与喷管喉径、喷管膨胀比之间必须满足的关系等;结构强度约束包括燃烧室材料、喷管材料等的刚度及稳定性的要求。以上各种约束的界限约束条件要求每个设计变量都要在一定的允许变化范围内优选，即有如下形式:

其中，ai、bi分别是所对应的设计变量的下限和上限。

2 基于改进遗传算法的优化求解

2.1 改进遗传算法

标准遗传算法在求解实际问题时往往会出现“早熟”现象，使得最终优化结果只是局部最优解，不能得到全局最优解，为抑制或缓解遗传算法的“早熟”现象，文中在标准遗传算法上做了相应改进，以提高其在工程中的应用性能。主要改进点有:1）编码方式采用二进制格雷编码，这种编码方式克服了二进制编码出现的海明悬崖问题，提高了算法的局部搜索能力。2）多增设了一个倒位操作，这种改进可以防止遗传算法在进化过程中过早陷入局部最优解，增加了个体的多样性，从而增强了算法的全局搜索能力。

2.2 改进遗传算法参数的选取

在遗传算法的运行过程中，存在对其性能产生重大影响的一组参数，这组参数在初始阶段或种群进化过程中需要合理选择和控制。主要包括种群规模N、交叉概率Pc、变异概率Pm和新增加的倒位概率Pl。

大规模的种群可以改进算法搜索的质量，防止早熟收敛。但大种群增加了个体适应度的计算量，使收敛速度降低，综合考虑，文中取种群规模为80。

交叉概率的选择决定了交叉的频率，频率越高，可以越快收敛到最有希望的最优解区域，但太高的频率也可能导致过早收敛，文中优化中取交叉概率为0.8。

变异概率和倒位概率是保持样本多样性的有效手段，分别取初始变异概率为0.05，倒位概率为0.05。

2.3 罚函数处理不等式约束问题

在使用遗传算法优化时，必须对约束条件进行处理，罚函数法是处理约束优化问题最常用的方法。在约束算法中，惩罚技术用来在每一代的种群中保持部分不可行解，使遗传搜索可以从可行域和不可行域两边来达到最优解。因此，利用遗传算法与罚函数结合，对上述发动机优化目标函数构造如式（4）所示的新目标函数，并将新目标作为新的适应度函数。

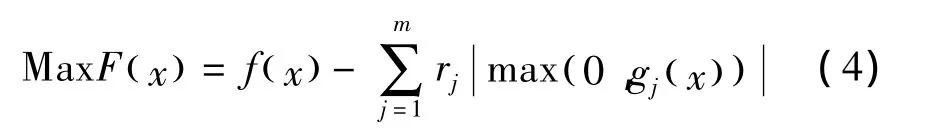
式中rj为惩罚因子。

基于改进遗传算法的发动机优化设计步骤如图2。

图2 改进遗传算法流程图

3 固体火箭发动机优化结果分析

计算中取发动机装药质量为0.24kg，采用双钴－2推进剂，密度为1.65g/cm3。各变量的取值范围为Di∈30，[]40;Pc∈［8.5，10］;α∈［12，15］;dt∈［10，15］;εA∈3，[]10;t∈［0.18，0.22］。进化代数取为800。

用改进遗传算法对个体火箭发动机进行寻优计算，在进化到500代左右时，算法基本收敛，各设计变量以及目标函数也均收敛到最优解。优化计算结果与优化前发动机数据对比见表1。

表1 遗传算法优化计算结果

由表1可以看出，遗传算法优化计算后的发动机重量比冲比优化前略有提高，为3%左右;在性能约束中，由于限制了通气参量最大值不超过110，所以优化后发动机的通气参量æ值相比原设计从119降到了105，降幅为11.76%，总体来讲，改进遗传算法优化计算后的结果比原始设计方案有明显提高。

4 结论

1）用遗传算法对固体火箭发动机总体参数进行优化设计，充分利用了遗传算法的全局搜索能力，很好解决了设计变量多并且关系复杂的困难，在给定空间里，得到了设计变量的最优解，使发动机体重量比冲和性能得到有效提高。

2）在工程实际应用中，用该方法进行小型固体发动机优化设计，可以避免对设计师经验的强烈依赖性，为设计经验不足者提供了有效的技术手段。

［1］周明，孙树栋.遗传算法原理及应用［M］.北京:国防工业出版社，1999.

［2］雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2005.

［3］王有元.固体火箭发动机设计［M］.长沙:国防工业出版社，1984.

［4］王鹏，李旭昌，徐颖军.固体火箭发动机总体优化设计［J］.火箭推进，2007，33（4）:16－19.

［5］何景轩，田维平，何国强，等.基于遗传算法的固体火箭发动机参数优化设计［J］.固体火箭技术，2004，27（4）:250－254.