基于人工蜂群支持向量机的模拟电路故障诊断

曾 涛，赵 岚

(1.燕山大学信息化处，河北 秦皇岛 066004;2.秦皇岛职业技术学院 机电工程系，河北 秦皇岛 066004)

0 引言

20世纪90年代，Vapnik等在统计学习理论(SLT)的基础上提出一种新型机器学习方法——支持向量机 (Support Vector Machine，SVM)。与神经网络等学习方法相比，支持向量机基于结构风险最小化原则，具有小样本学习、泛化能力强等特点，能有效地避免过学习、局部极小点以及“维数灾难”等问题[1，2]。目前，SVM 的实用算法研究、设计和实现都已取得了丰硕的成果，并且广泛应用于故障诊断、数据挖掘、文本识别[3]等领域。但是支持向量机的参数选择决定了其学习性能和泛化能力，由于在参数的选择范围内可选择的数量是无穷的，在多个参数中盲目搜索最优参数是需要极大的时间代价，并且很难逼近最优。针对支持向量机的参数选择问题，很多学者进行了大量的研究，文献[4]在分析了几种评估SVM性能的方法之后，利用梯度下降法对SVM参数进行优化，取得了较好的效果，但是梯度下降法容易陷入局部极小值。文献[5]利用Bootstrap方法建立的支持向量机的评估函数，利用模拟退火算法对参数进行了优化。文献[6，7]分别利用蚁群优化算法与小生境遗传算法对SVM核参数进行优化，都取得了较好的结果。

蜂群算法是建立在蜜蜂自组织模型和群体智能基础上的一种非数值优化计算方法[8]。文献[9]对蜂群算法在解决组合优化问题中的原理和应用方法，并将其应用于旅行商问题 (TSP)等问题。本文将人工蜂群算法应用于支持向量机的参数优化当中，对其应用方法进行了详细的阐述，并利用UCI数据库中的数据对其进行了仿真，最终将其用于模拟电路故障诊断当中，取得了较好的效果。

1 支持向量机及其参数分析

1.1 支持向量机

支持向量机就是寻找一个最优分类超平面，即最大间隔超平面。训练集为非线性时，通过一个非线性函数φ(x)将训练集数据x映射到一个高维线性特征空间，在这个维数可能为无穷大的线性空间中构造最优分类超平面，并得到分类器的决策函数。

对于二类分类情况，训练样本集为

为了找到最优超平面，必须求解下列二次优化问题:

式中:*表示内积;ω为系数向量;ξi≥0为考虑到存在一些样本不能被正确分类，为了保证分类的正确性，而引入的松弛变量;C称为惩罚因子，通过改变惩罚因子可以在分类器的泛化能力和误分类率之间进行折衷。

其对偶问题为一个凸二次规划问题，具有全局最优解，从而避免了局部极小点的问题。

最终可以得到决策函数:

构造这一类决策函数的学习机器称为支持向量机。支持向量机的结构示意图如图1所示[10]。

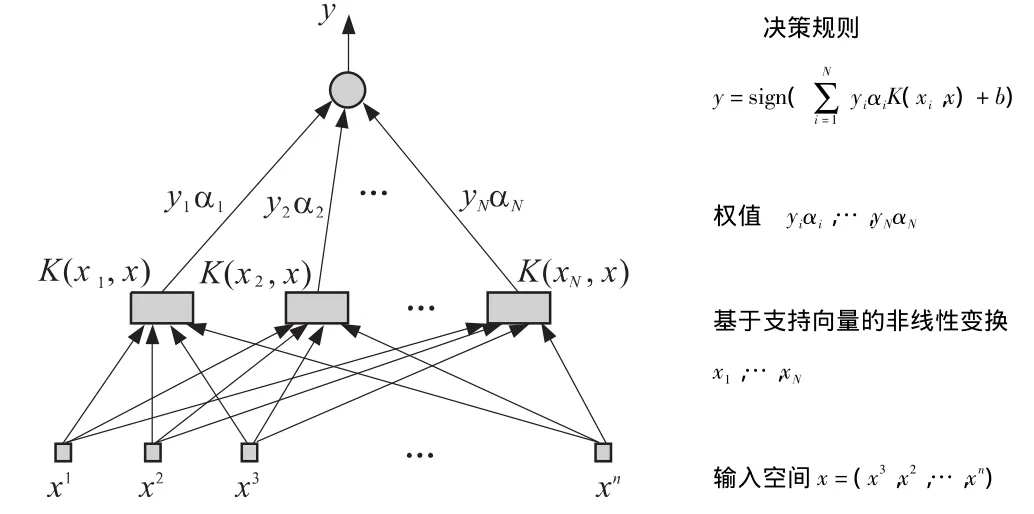
图1 支持向量机结构图Fig.1 Structure block of support vector machine

1.2 参数分析

支持向量机的性能依赖于多个参数，其中惩罚因子C，控制间隔的最大化与分类误差之间的折衷，C越大，则对于错分样本的惩罚越大。其他的参数出现在非线性映射函数中的核参数，影响样本在高维特征空间的分布情况，如RBF函数中的γ，核参数的改变实际上隐含着改变了映射函数，即改变了特征空间的VC维，从而影响置信范围，最终影响结构风险范围。为了简单，将它们统称为核参数，这样就可以将它们在一个统一的框架内处理。

2 蜂群算法的基本原理

人工蜂群算法 (Artificial Bees Colony，ABC)是近年来根据自然界密封群体的搜集食物，即采蜜过程的模拟而提出的一种群算法。蜂群采蜜行为主要包括3个基本部分:蜜源、采蜜蜂、待工蜂。此外引入3种基本的行为模式:搜索蜜源、为蜜源招募和放弃蜜源。

(1)蜜源。蜜源代表各种可能的解。

(2)采蜜蜂。采蜜蜂携带了具体的蜜源信息，这些信息包括蜜源与蜂巢的距离、蜜源方向、蜜源的收益度;采蜜蜂通过摇摆舞与其他蜜蜂分享这些信息，按一定比例，部分成为引领蜂。

(3)待工蜂。待工蜂可以分为侦查蜂、跟随蜂。侦查蜂搜索蜂巢附件的新蜜源。跟随蜂在蜂巢内等待，通过分享采蜜蜂的信息，寻找蜜源。开始时，待工蜂没有蜂巢附近蜜源的信息，因此有两种选择:(a)待工蜂可以作为侦察蜂，由于某一内部激励或可能的外在因素，开始自发地搜寻在蜂巢附近的蜜源。(b)在观察到其他蜜蜂摇摆舞后，它可被招募并按照获得的信息寻找蜜源。待工蜂发现新的蜜源后，记住蜜源的位置，并迅速开始采蜜，此时，待工蜂变成了采蜜蜂。蜜蜂采蜜回到蜂箱卸蜂后，有以下几种选择:(a)放弃蜜源，成为待工的跟随蜂;(b)返回同一蜜源前，跳摇摆舞招募蜂巢其他伙伴。(c)不招募其他蜜蜂，继续采蜜。初始时刻，蜜蜂均无任何先验知识，都是侦察蜂。随机搜索到食物源后，侦察蜂返回蜂巢的舞蹈区，根据食物源收益度的相对大小，侦察蜂可以转变为上述任何一种蜜蜂，原则如下:

(1)所采集食物源的收益度相对很低时，它可以再次成为侦察蜂搜寻附近的食物源。其转变结果是放弃上次采集的食物源。

(2)所采集食物源的收益度排名小于临界值(如排名在后50%)时，它可以在观察完舞蹈后成为跟随蜂，并前往相应的食物源采蜜。

(3)所采集食物源的收益度排名高于临界值时，它成为引领蜂，继续在同一食物源采蜜，并在舞蹈区招募更多的蜜蜂采集相应食物源。

3 基于人工蜂群优化算法的SVM参数选择

ABC算法正是受此启发，该算法基本思路如下:在循环开始时，所有的人工蜂均在蜂巢。在搜索过程中每个人工蜂都做局部的搜索，从而逐步增加可行解。在每一步的搜索过程中，其中的一个或者多个最优解都被保存下来，最终通过决策分析得到最优解。根据人工蜂群算法和支持向量机参数寻优的特点，其基本思路如下:

Step 1:确定人工蜂群的群体数量，即蜂群中蜜蜂总数，设为B。确定侦查蜂占群体数量的比例，一般大于10%，易于收敛，侦查蜂数量为SN。

Step 2:开始时刻，所有蜜蜂均成为侦查蜂，在给定范围内随机确定B个蜜源，即随机选择B个 (C，γ)的组合参数。

Step 3:计算这B个蜜源的品质，初始蜜源的品质由其单点的分类准确率决定。对于蜜源品质低的情况，侦查蜂可以继续作为侦查蜂继续搜索蜜源，也可以作为跟随蜂去较高品质的蜜源进行采蜜;根据蜜源品质，跟随蜂按照一定的比例跟随到各个蜜源进行采蜜。

Step 4:跟随蜂到达各个蜜源后，在蜜源附近的连续区域进行采蜜，以确定在这一蜜源的最优品质点。其中蜜源附近各个蜜源点的确定方式采用下式确定:

式中:xmax和xmin决定了要搜索的蜜源区域范围。

Step 5:蜂群回到蜂巢后，计算各个蜜源的品质，重新分配各个蜜源的采蜜蜂数量。计算蜜源品质的方法:a.蜜源中最好的品质点，即其中最优的分类准确率;b.蜜源区域所得的品质平均值，即所有分类准确率的平均值。

循环上述步骤，最终得到最优的蜜源点，即得到最优的SVM参数。

4 仿真及分析

首先，利用 UCI[11]数据库中的 Ionosphere，Haberman，Dermatology和Vehicle数据对本方法进行仿真验证。其中核函数选择RBF核函数，即需要选择的核参数位惩罚参数C和宽度参数γ。在Matlab环境下对其进行仿真。人工蜂群的参数选择如下:蜂群数量为100，侦查蜂的比例为20%。文中同时利用网格搜索的方式进行参数的搜索，以和人工蜂群搜索结果进行对比，其中参数范围选择为 C=(2-5，2-4，…，28)，γ =(2-5，2-4，…，25)。最终仿真结果如表1所示。

表1 UCI数据仿真结果Tab.1 Simulation results of UCI data

由仿真结果表明，人工蜂群算法相对于网格搜索的方法能够较好地对支持向量机参数进行优化。

将人工蜂群优化参数的支持向量机用于模拟电路的故障诊断。本文采用ITC’97[12]中的Elliptical滤波器标准电路对本文方法进行仿真验证。图2所示为文中用到的Elliptical滤波器电路原理图。表2所示为电路中各个元器件的标称值。在Pspice环境下对电路进行正常状态和故障状态的仿真。表3给出了设置故障的方式，这里均采用原件的软故障，即元器件标称值上升或下降50%。

图2 Elliptical滤波器原理图Fig.2 Schematic diagram of Elliptical filter

表2 元器件标称值Tab.2 Nominal value of components

表3 电路故障设置方式Tab.3 Setting mode of circuit fault

对电路正常状态和所有设置故障状态进行30次Monte-Carlo分析，得到输出信号。这里采用3个运放的输出信号作为故障诊断信号。对采集信号进行小波变换以进行特征提取，利用信号的各频段的频谱能量作为诊断特征进行诊断。通过小波特征提取，得到330个样本，每类30个样本，这里利用每类中的20个样本训练，另外10个样本作为验证样本。

利用ABC-SVM对电路得到的特征样本进行训练和验证。仿真结果如下:C=95.616 9，γ=0.796 7，分类准确率达到99.09%。以上结果表明，基于人工蜂群算法优化参数的支持向量机能够较好地实现对模拟电路的故障诊断。

5 结论

针对支持向量机中的参数优化问题，本文引入了人工蜂群算法。利用人工蜂群算法的全局优化特性对支持向量机的参数进行了有效的选择。最终将人工蜂群支持向量机用于模拟电路故障诊断，有效得到了故障分类器的最优参数，从而提高了模拟电路故障诊断准确率。但是本文中只是利用人工蜂群算法对支持向量机的参数进行了选择，由于参数和特征选择是密切相关的，因此对其进行联合优化是以后的研究方向。

[1]张倩，杨耀权.基于支持向量机核函数的研究[J].电力科学与工程，2012，25(5):42-45.Zhang Qian，Yang Yaoquan.Research on the kernel function of support vector machine[J].Power Science and Engineering，2012，25(5):42-45.

[2]祖文超，李红君，苑津莎.基于纠错能力的SVM在变压器故障诊断的应用[J].电力科学与工程，2012，28(11):39-43.Zu Wenchao，Li Hongjun，Yuan Jinsha.Application of transformer fault diagnosis based on the error-correcting codes capability of SVM[J].Power Science and Engineering，2012，28(11):39-43.

[3]Wang T Y，Chiang H M.Fuzzy support vector machine for multi-class text categorization[J].Information Processing and Management，2007，43:914-929.

[4]Chapelle O，Vapnik V，Bousquet O，et al.Choosing multiple parameters for support vector machines[J].Machine Learning，2002，(46):131-159.

[5]赵春秀，周辉仁，刘春霞.基于SA和Bootstrap的LSSVM参数优选及应用[J].统计与决策，2008，(15):25-28.

[6]刘春波，王鲜芳，潘丰.基于蚁群优化算法的支持向量机参数选择及仿真[J].中南大学学报 (自然科学版)，2008，39(6):1309-1313.Liu Chunbo，Wang Xianfang，Pan Feng.Parameters selection and stimulation of support vector machines based on ant colony optimization algorithm[J].Journal of Central South University(Science and Technology)，2008，39(6):1309-1313.

[7]朱宁，冯志刚，王祁.基于小生境遗传算法的支持向量机分类器参数优化[J].南京理工大学学报 (自然科学版)，2009，33(1):16-20.Zhu Ning，Feng Zhigang，Wang Qi.Parameter optimization of support vector machine for classification using niche genetic algorithm[J].Journal of Nanjing University of Science and Technology(Nature Science)，2009，33(1):16-20.

[8]胡中华，赵敏.基于人工蜂群算法的TSP仿真[J].北京理工大学学报，2009，29(11):978-982.Hu Zhonghua，Zhao Min.Simulation on traveling salesman problem(TSP)based on artificial bees colony algorithm[J].Journal of Beijing Institute of Technology，2009，29(11):978-982.

[9]Teodorovic D，Lucic P，Markovic G，Dell'Orco M.Bee colony optimization:principles and applications[C]，2006:151-156.

[10]Vapnik.统计学习理论[M].许建华，张学工译.北京:电子工业出版社，2004.

[11]Blake C L，Merz C J.UCI repository of machine learning databases.Univ.Clifornia，Dept.Inform.Comput.Sci.，Irvine，1998.

[12]Kondagunturi R，Bradley E，Maggard K，et al.Benchmark circuits for analog and mixed-signal testing[C].1999.