循环流化床锅炉床温的传递函数智能建模方法
王利杰,孙 明,程 希,殷立国,孙 剑
(1.河北省电力公司 电力科学研究院,河北 石家庄 050021;2.华北电力大学 科技学院,河北 保定 071051;3.保定供电公司,河北 保定 071000;4.中国大唐集团公司,北京 100033;5.中国核动力研究设计院,四川 成都 610041)
0 引言
提高煤的利用效率和控制污染物排放是燃煤发电技术发展的主要目标。循环流化床 (CFB)燃烧技术和燃气-蒸汽联合循环 (IGCC)发电技术是公认的最有前途的两种清洁煤燃烧发电技术。循环流化床锅炉与煤粉炉的主要区别在于原煤经过破碎以大颗粒形式直接送入炉膛,经过炉内小循环和炉外大循环的反复长时间燃烧,达到较高的燃烧效率。为了保证燃烧的稳定性和循环的持续性,燃煤CFB锅炉炉膛内部都有大量不可燃固体颗粒,一般占到炉膛总物料量的97%以上。这些固体颗粒直接造成了炉内燃烧过程的大热惯性,这也是CFB锅炉燃烧系统自动控制的难度所在,也是热工自动控制领域的研究热点。国内文献中所提到的CFB机组90%以上的自动投入率,往往是在某稳定工况点时的自动投入率,并不是大范围负荷变动时的自动投入率。从被控对象特性来看,CFB锅炉燃烧系统具有多变量、非线性、强耦合、时变、大惯性、分布参数等特点,是一类典型的难控的热工对象。为了解决CFB锅炉自动控制的瓶颈,需对现有控制系统进行优化设计从而提高控制水平,其首要工作是深刻理解流化态燃烧的特性,建立CFB锅炉燃烧系统的实用模型。因此,建立正确反映对象特性又能满足实时性要求的动态数学模型已成为研制和完善循环流化床自动控制系统的迫切需求。本文分析了目前国内外在CFB锅炉燃烧系统建模问题上的主要研究方法,提出:依据机组运行的历史数据,挖掘该数据进行传递函数建模,并用历史数据进行模型的检验。本文主要目标是定量化描述CFB机组燃烧系统的动态特性,为控制器优化提供依据,为同类机组优化提供参考方法,为运行提供指导。
1 循环流化床燃烧过程的两种建模方法
1.1 机理建模
近20多年来,不少研究人员在建立CFB机理数学模型上做了很多工作。根据对燃烧室的不同解释和假设,依据物质质量平衡、能量平衡和流体动力学特性建立了不同的数学模型。
总体来说,各燃烧数学模型的主要差别在于对上升通道流体动力学模型 (气固流动模型)以及与之对应的总物料平衡的描述上。按照流动模型的不同,可以将循环流化床数学模型分为鼓泡床模型、拟流体模型、区段模型、颗粒轨道模型和多维模型;按照建模机理分类,分为基于经验的半关联性质的模型和基于微观守恒方程的机理模型;按照简化程度分类,可分为零维、一维、二维、三维等模型。这些动静态模型影响最广和最显著的特点是采用小室 (Cell或Compartment)模型的求解方法。比较出名的是清华大学的李政等建立的CFB锅炉整体数学模型以及随后简化得出的CFB锅炉实时动态数学模型:根据氧气质量平衡、残碳动态燃烧过程的碳质量平衡、挥发分燃烧及残碳燃烧的动态能量平衡以及以排渣量为主动操作量的动态床料质量平衡方程,将炉膛分为30个小室,分别计算固体浓度、压降型线以及传热系数。该模型能有效地模拟CFB锅炉燃料的动态积累和燃烧过程,并且成功应用于CFB锅炉培训仿真机中[1~5]。
需要指出的是,这些机理模型都是基于表象的宏观解释,不同的流体动力学假设得出不同的燃烧模型。一个合适的流体动力学模型是循环流化床模型成功的关键,而直至目前,对循环流化床的流动、传热、反应以及颗粒碰撞等微观机理的了解还是不透彻的。这些模型加深了人们对循环流化床燃烧过程的认识,但是面向控制器的设计和优化还有一段距离。同时,在CFB机组仿真机的研制中,由于对某些机理的认识不清,往往出现根据现象和经验人为去凑机理模型的情况。所以,CFB机组的机理模型还仅仅被用于培训仿真机中。
1.2 基于数据的非参数模型
对CFB燃烧系统热工过程的模型辨识是实现其自动控制的基础。鉴于目前从机理方向建立的CFB燃烧过程模型距离进行控制系统优化设计的目标还太远,很多学者都从工程角度考虑,通过阶跃扰动实验建立了某些子系统的传递函数模型,或者通过实际运行数据建立起智能模型,如神经网络模型或模糊系统模型等,然后初步进行了所感兴趣系统的控制设计[6~8]。这些模型有些需要进行大量试验,并且大多是对某个单独系统或者在某个单独工况点的建模,没有一个整体的完整考虑整个燃烧系统的实际模型,在控制系统的优化设计上也大多停留在仿真阶段。同时,国内对于300 MW大型CFB机组的燃烧系统建模研究目前还是空白 (国内三大锅炉厂于2003年同时引进法国阿尔斯通大型循环流化床技术,目前该技术是国内大型CFB机组的主力)。作者长期深入某已建成的大型CFB燃煤电厂,通过生产实际得到大量运行经验,从而遴选出部分能够代表燃烧系统动态特性的运行数据,利用群体智能算法拟合出各个工况点的线性传递函数模型,并进行模型验证,以期在CFB燃烧机理方式之外加深对流化床燃烧本质的认识。这种方式获取数据的质量以及有效性取决于机组运行数据的丰富性以及工程人员对被控对象特性的了解程度、对数据挖掘的人为经验,但是它的优点是对工业生产没有影响、数据量丰富、具有说服力。
2 传递函数模型的参数辨识过程
2.1 嵌入燃烧过程的传递函数模型表达
大部分复杂热工对象都具有非线性、参数时变等特征,要建立一个全范围适用的模型是不易的。工业控制中常用的方法是,将对象的运行范围划分为几个独立的工作点,在工作点附近用传递函数表示对象的动态特性。传递函数模型一般是由惯性环节、延迟环节、积分环节以及正零点形式等组成,如下式:
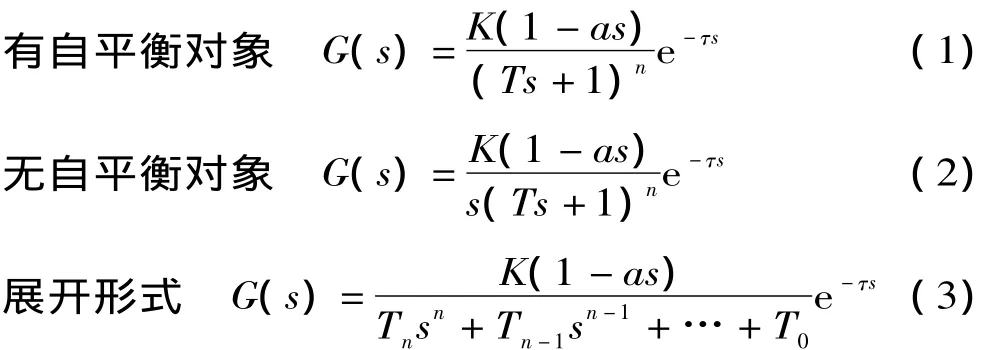
对这些模型进行计算机仿真时,式 (1)和式 (2)要比式 (3)容易离散化,计算速度更快。对CFB锅炉燃烧系统进行建模时,式 (1)和式 (2)被选择为待辨识的备选模型集。
CFB锅炉燃烧系统调整的目标是合理调整锅炉的给煤量、进石灰石量、送风量、给水量以及设置合适的风压,使锅炉生产的主蒸汽以及再热蒸汽在量和质上满足汽轮机做功的需要,同时稳定其燃烧过程。国内引进ALSTOM技术制造的300 MW循环流化床锅炉采用岛式半露天布置、单锅筒自然循环、绝热式旋风分离器、裤衩腿结构、外置式换热器等建造形式。对于这种锅炉,维持床温稳定、保持合适的料层厚度、保证两侧裤衩腿的流化均匀是核心任务。燃烧系统建模的最重要内容就是分别获取床温、床压与其影响因素的关系以及主汽压力与燃料量的关系。现以床温为例,其主要影响因素如图1所示。
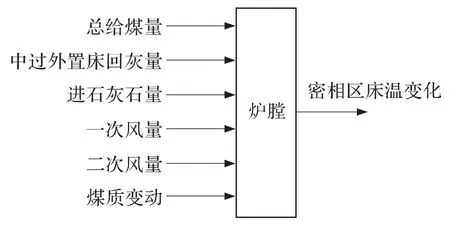
图1 床温的主要影响因素Fig.1 Main factors affecting bed temperature
这是一个多输入单输出 (MISO)的系统。为了简化,可以将其看成多个单输入单输出 (SISO)的系统叠加的形式。对于每个SISO系统,辨识其数学模型的过程可以定义为根据辨识测试或实验获得能够反映输入与输出之间因果关系的数据,加以必要的数据处理,指定系统的共同性质来获得一个备选模型集,从这个模型集中选择一个合适的模型,通常是使某个误差准则 (损失函数)最小化,如图2。对于MISO系统,辨识的过程也是一样的,只不过备选模型集是多维模型集,通常需要对每个SISO系统有一个粗略的认识或者辨识结果,这样才能学习出一个满意的MISO模型。
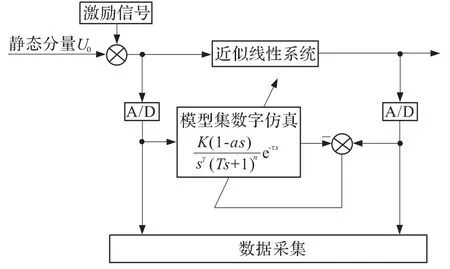
图2 辨识过程示意图Fig.2 Diagram of identification process
2.2 群体智能算法用于参数辨识
在模型集确定且输入输出数据已经得到的情况下,CFB燃烧系统传递函数的求解实际上是一个系统辨识问题。辨识就是通过分析对象在输入作用下的响应,估计出对象的数学模型,即估计出式 (1)、(2)中的K,a,T,n,τ的一个合适组合,是参数寻优问题。其中,n,τ属于结构参数,K,a,T属于过程参数。本文对传递函数的结构参数辨识采用遍历法,过程参数采用计算简便、有着优良全局搜索能力的粒子群算法(PSO)。
PSO算法描述如下:随机初始化一群粒子,其中,第i个粒子在D维解空间的位置表示为xi=(xi1,xi2,…,xiD)。每一次迭代,粒子通过动态跟踪两个极值来更新其速度和位置。第一个是粒子从初始到当前迭代次数搜索产生的最优解:个体极值pBesti= (pi1,pi2,…,piD);第二个是粒子种群目前的最优解:全局极值gBest=(g1,g2,…,gD)。第i个粒子根据以下公式来更新其第d维 (1≤d≤D)速度和位置:
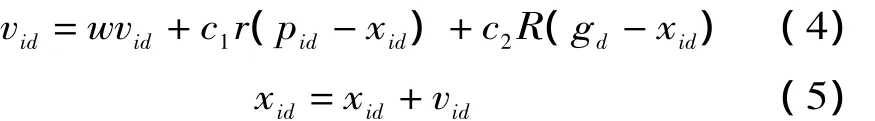
式中:vid代表粒子速度;xid代表粒子位置;w是为避免粒子在全局最优解附近震荡的可变惯性系数;r,R是均匀分布在 (0,1)区间的随机数;c1,c2是学习因子。粒子在解空间内不断跟踪个体极值和全局极值进行搜索,直至达到规定的迭代次数或满足规定的性能指标为止。算法流程如图3。
2.3 热工过程的计算机仿真
利用粒子群算法辨识燃烧系统传递函数参数时,需要计算某种参数组合情况下系统的适应度值,这涉及到适应度函数的选取和待选模型集的数字计算。将连续模型变换为离散化的差分方程,常用的方法有离散相似法和数值积分法,其中数值积分法又分为欧拉法、梯形法、龙格-库塔法、阿达姆斯法等等,它们的运算速度都较快。需要指出的是,数学计算软件Matlab中也有用于连续系统离散化的现成软件包 (如c2d函数),但是输出的差分方程中包含了多个k时刻之前的输出数值,不利于仿真,并且运算速度较慢。文中采取的办法是对复杂传递函数技巧性拆分,利用离散相似法得到能快速运算的差分方程。例如,式(2)可以看作图4形式:
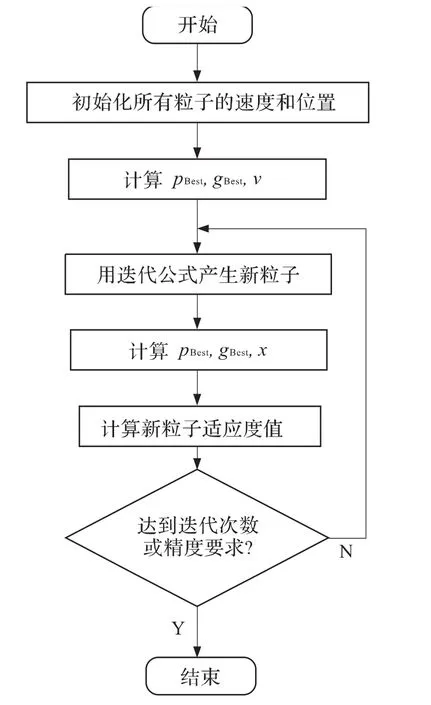
图3 粒子群优化算法计算流程Fig.3 Calculating process of PSO algorithm

图4 逆向响应系统传递函数的拆分Fig.4 Transfer function split of the reverse response system
采用离散相似法,各环节前均加入离散-再现环节,并设ΔT为虚拟采样周期,则有:
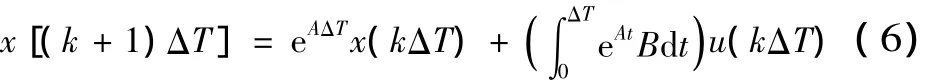
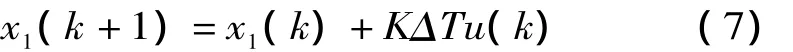
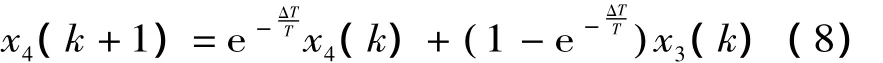
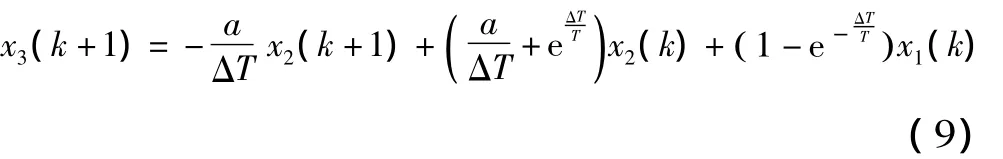
利用公式 (7),(8),(9),对象 (1),(2)就能在计算机上高速仿真。
2.4 数据的有效性
用于模型辨识的数据能不能正确反映输入输出之间的关系是辨识结果好坏的关键。利用运行数据进行模型辨识首先需要对被控对象的结构和特性有深刻认识,确定关键的变量;其次观察对比大量历史曲线,遴选出可用的数据,剔除坏的数据和无价值的数据,选择标准需要注意以下几点:
(1)传递函数的定义是在某一初始状态下输出对输入的转移能力,是针对偏差的转移能力,所以输入数据应有一定的起伏,太小的数据波动会被干扰噪声淹没。
(2)对于SISO系统,输出变量的波动应该是由输入变量单独引起的,这就要求观察所有输出变量的影响因素。另外,需要根据经验判断输出变量的响应是否是对输入变量的正确反应。分析图5左上图:由于前期给煤量偏少,在带较高负荷时,床上密相区焦炭库存的消耗量大于添加量,床温具有下降趋势。在运行人员为了稳住床温突然增加给煤量时,由于挥发分的快速燃烧,床温不至于下降太快,但是焦炭池的累积却是需要一个长期的过程。所以,由图中可以看出,虽然给煤量增加了8%之多,但是床温却是波动中略有下降,波动部分反映的是给煤量的短期变化所带来的挥发分变化以及细粒子的变化,下降部分反应的是焦炭池的消耗与蓄积平衡。这段动态过程中的其他影响因素的变化如图5。用于调节床温的中过外置床灰控阀有一个不到2%的阶跃扰动,影响可以忽略不计,一次风量、二次风量、总风量 (一次风量、二次风量、流化风量之和)都没有太大变化,即时煤耗 (给煤量和参考功率之比)变动在0.62~0.68之间,基本可以认为给煤的单位发热量没变。
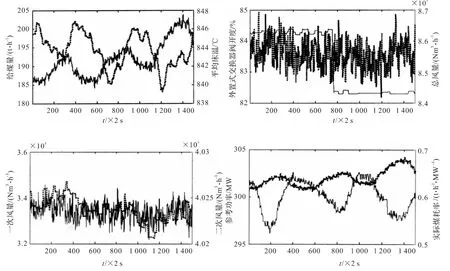
图5 床温影响因素曲线Fig.5 The affecting factor's curve of bed temperature
(3)燃烧系统本质上是非线性的。为了建立线性化模型,所有参数的变化都必须是在对象可近似线性化的范围内。线性工况点的划分,依靠的是经验和多次试验得到的结论。
(4)数据的采样周期应兼顾计算量和精度两方面要求。为了使被采样信号无失真地再现,采样频率应满足香农定理。可根据下述一个经验公式,设置采样周期其中,n是被控对象传递函数阶次,T是被控对象传递函数的时间常数,ts是采样时间。另一个经验公式是根据系统的调节时间来确定采样时间,令T95是系统调节时间的95%,采样时间ts可以取为
(5)采样数据段最好起始于某个稳定工况点,即数据序列反映的是系统从某一静态开始的动态过程,这样便于在辨识工作时确定所采样数据的静态分量。
(6)采样数据中一般都包含了测量噪声和其他非过程干扰,在进行辨识工作之前要进行数据预处理。常用的数学滤波方法有一阶低通滤波、一阶高通滤波、递推平均滤波、五点三次平滑滤波和程序判别滤波等。
3 基于运行数据的燃烧过程建模
3.1 燃料量到床温的过程分析
新的煤颗粒被送入流化床锅炉后,立即被大量灼热的不可燃床料包围并加热至床温;加热速率一般在100~1 000℃/s的范围内。这个加热过程所吸收的热量只为床层总热容量的千分之几,对床层温度的影响很小。当煤粒升温到一定温度时,煤将发生热解反应而释放出挥发分。由于密相区处于还原性气氛,几乎达到一半的挥发分是在炉膛稀相区燃烧而对床温的贡献并不大。挥发分析出的过程中,煤颗粒的物理化学特性发生急剧变化,部分较大粒径的煤颗粒会发生由于挥发分逸出产生的压力和空隙网络中挥发分压力增加而引起的所谓一级破碎过程。当煤粒中的挥发分被加热析出后,未被一次燃烬的煤往往转化为焦炭颗粒或外层为焦炭、内部仍为煤的颗粒。碳颗粒的燃烧速度比挥发分低得多,一般挥发分在十几s之内就能完成析出和燃烧过程,而焦炭颗粒虽然要经历二级破碎和磨损等有利于燃烧的过程,其循环燃烬时间往往需要几 min 乃至十几 min[10~13]。
循环流化床炉内的床料绝大部分是惰性、灼热的灰渣,可燃物只占不到5%的份额,床内物料无论是加热还是冷却都是一个漫长的过程。从前面分析可知,在循环流化床燃烧方式下,燃料热量的释放分两个过程,先是挥发分的燃烧,后是焦炭的燃烧,热源的多少并不取决于即时输入燃料量的多少,而是取决于床内焦炭库存的多少,而焦炭的库存量反映的是过去一段时间内的输入燃料量和燃烧消耗的平衡关系。总体上说,燃料量变化引起床温变化的过程是一个具有滞后、惯性和自平衡能力的过程。
3.2 传递函数模型及模型检验
图6是某300 MW循环流化床燃煤电厂某段时间内总给煤量和平均床温的变化曲线。锅炉型号是SG-1060/17.5-M802,为亚临界中间再热,单锅筒自然循环、循环流化床锅炉,即时燃料为设计煤种 (洗中煤∶煤矸石=60∶40混烧),煤种分析见表1。采样数据说明如下:采样时间为2 s,总给煤量为4台刮板给煤机煤量反馈值之和;平均床温为6个床温信号的平均值,这6个床温信号分别代表左右裤衩腿密相区上中下床层的温度,每个温度值由3个热电偶测点取中值得到;采样数据时间段内锅炉没有投入石灰石粉;给煤量单位为t/h,床温单位为℃;采样数据段内总给煤量变化20%,中过外置床回灰阀门变动10%,总风量变化1.7%,一次风量变化6.2%,二次风量持续增加7.5%,瞬时煤耗变化小于10%;经分析,可以认为床温变化主要由给煤量变化引起。
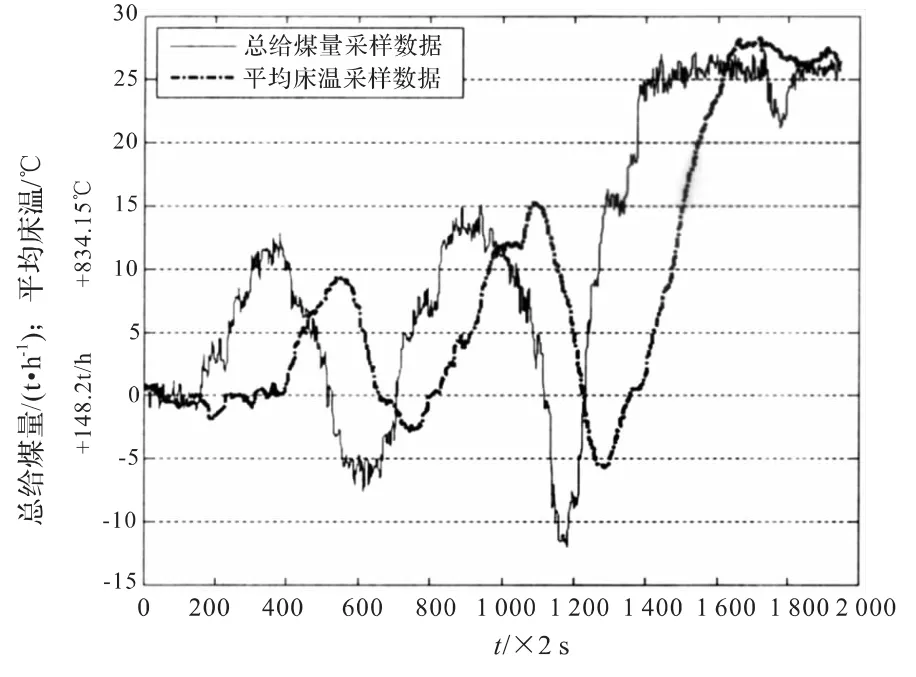
图6 辨识数据Fig.6 Sample data for identification
利用前述方法学习得到传递函数为:
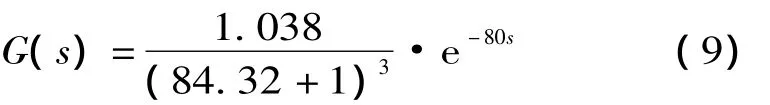
同样输入下,辨识模型输出和真实输出曲线如图7,均方误差为4.461 6。辨识模型基本能反映输入数据和输出数据的数学关系,但是并不证明该模型就能表示给煤量和平均床温在该工况点下的热工特性,必须经过与学习数据无关的数据的验证。验证数据如图8,采样时间为4 s,输入输出变量与学习数据一致。以验证数据为输入时,传递函数模型的输出和锅炉实际输出如图9,均方误差为1.500 4。
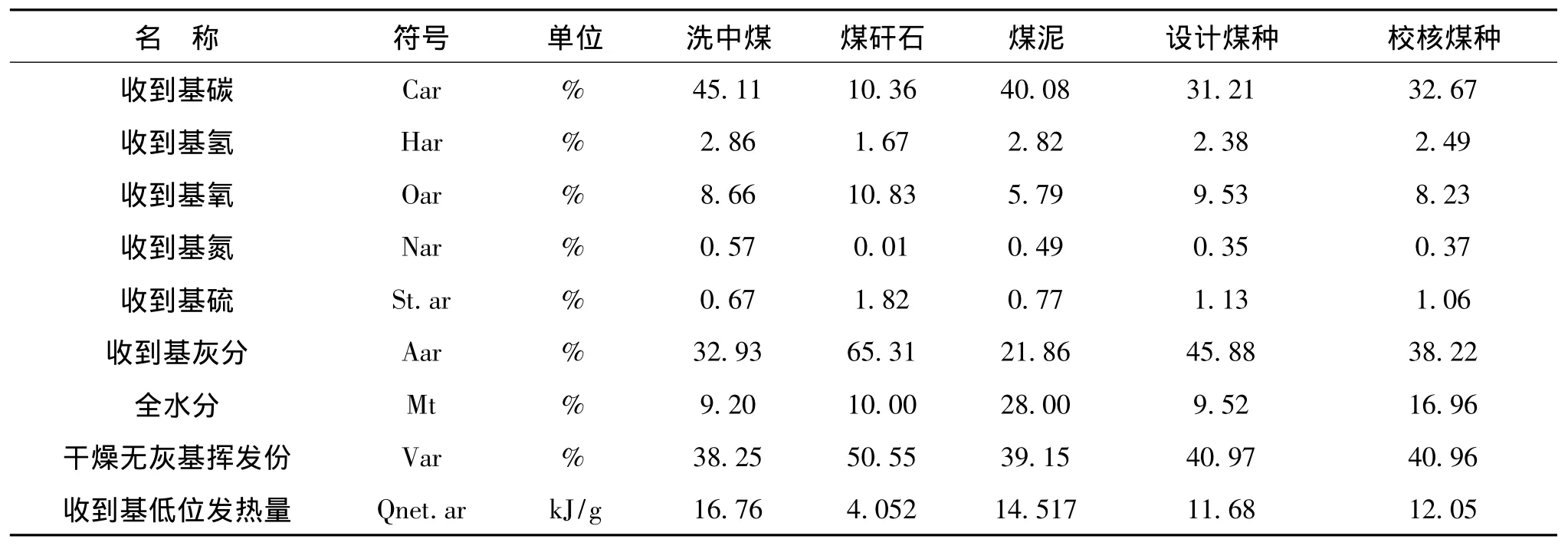
表1 煤质分析Tab.1 Feed coal quality analysis
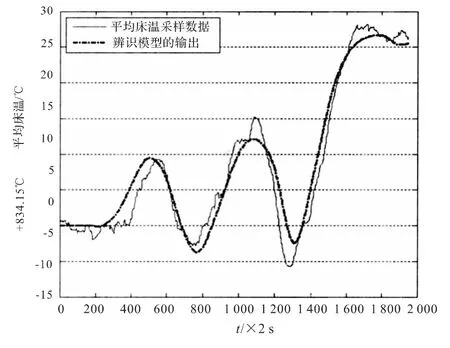
图7 辨识结果Fig.7 Results of identifying process
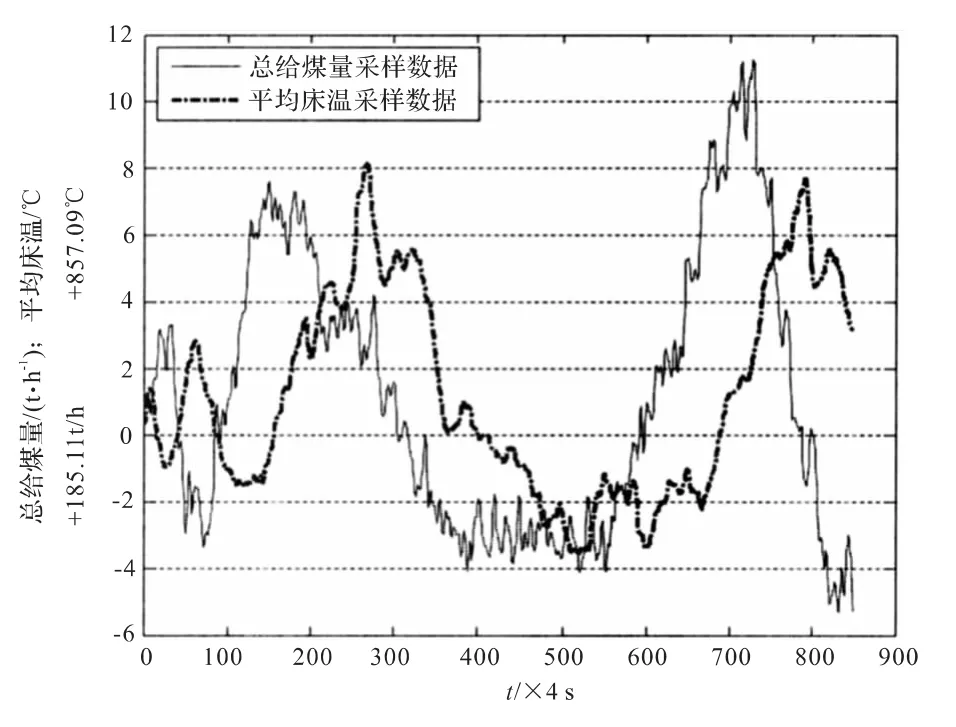
图8 验证数据Fig.8 Sample datas for verification
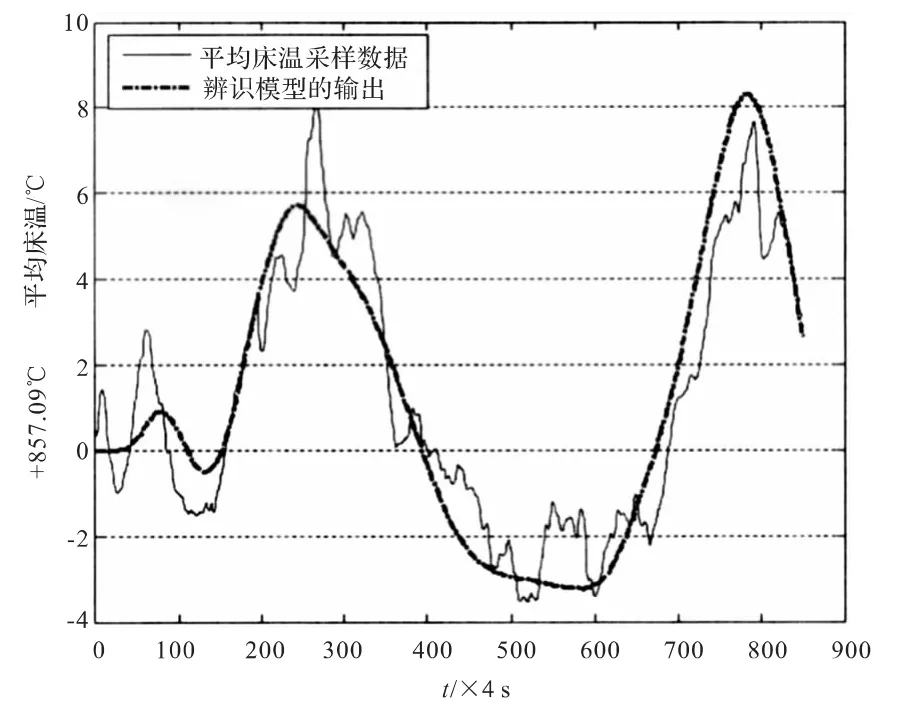
图9 验证结果Fig.9 Results of verifying process
4 结论
通过上述分析认为,根据人为经验挖掘运行数据,利用智能算法进行参数辨识,完全能够得到循环流化床锅炉各个工况点下的线性传递函数模型;该模型完全能够表征具体某台锅炉最近一段时间内的热工特性,能为后续的控制器优化提供数学依据;方法简单清晰,且数据获取方式容易。将多个SISO系统传递函数模型叠加就得到燃烧系统的MISO模型,将所有线性工况点模型组合在一起就得到燃烧系统在整个运行范围的热工特性数学模型。利用得到的数学模型总结分析流化态燃烧的特点,验证流化态燃烧机理的正确与否,分析具有裤衩腿结构CFB锅炉的建模特殊性,这些是进一步的研究方向。
[1]肖显斌,杨海瑞,吕俊复,等.循环流化床燃烧数学模型[J].煤炭转化,2002,25(3):11-16.Xiao Xianbin,Yang Hairui,Lu Junfu,et al.Mathematical modeling of combustion system in circulating fluidized bed boiler[J].Coal Conversion,2002,25(3):11-16.
[2]李政,倪维斗,王哲,等.循环流化床实时动态数学模型研究[J].动力工程,1999,19(2):33-36.Li Zheng,Ni Weidou,Wang Zhe,et al.A real time dynamic mathematical model of CFBC[J].Journal of Power Engineering,1999,19(2):33-36.
[3]李政,王哲,倪维斗.循环流化床全工况实时动态数学模 型 的 研 究[J].动 力 工 程,2000,20(1):511-514.Li Zheng,Wang Zhe,Ni Weidou.Study of full working scope dynamic mathematical model for CFBC[J].Journal of Power Engineering,2000,20(1):511-514.
[4]李政.循环流化床锅炉通用整体数学模型仿真与性能预测[D].北京:清华大学,1994.
[5]王勤辉,骆仲泱,李绚天,等.循环流化床锅炉炉内流动和燃烧特性的理论模型[J].动力工程,1999,19(4):269-274.Wang Qinhui,Luo Zhongyang,Li Xuantian,et al.Characteristics of fluid dynamics and combustion in a circulating fluidized bed boiler furnace-theory and model[J].Journal of Power Engineering,1999,19(4):269-274.
[6]马素霞,张建春,牛建斌,等.75t/h循环流化床锅炉变工况热态实验研究[J].动力工程,2005,25(3):348-351.Ma Suxia,Zhang Jianchun,Niu Jianbin,et al.Test studying a 75t/h circulating fluidized bed boiler under various modes of hot state operation[J].Power Engineering,2005,25(3):348-351.
[7]马素霞,薛亚丽.循环流化床锅炉燃烧系统的多变量控制[J].动力工程,2007,27(4):528-532.Ma Suxia,Xue Yali.Multi-variable control of circulating fluidized boilers'combustion system[J].Power Engineering,2007,27(4):528-532.
[8]席学军,姜学智,李东海,等.循环流化床锅炉燃烧系统的自抗扰控制[J].清华大学学报 (自然科学版),2004,44(11):1575-1579.Xi Xuejun,Jiang Xuezhi,Li Donghai,et al.Auto disturbance rejection control for circulating fluidized bed boiler combustion system[J].Journal of Tsinghua University(Science& Technology),2004,44(11):1575-1579.
[9]韩璞,罗毅,周黎辉,等.控制系统数字仿真技术[M].北京:中国电力出版社,2007.
[10]赵伟杰,王勤辉,张文震,等.循环流化床锅炉控制系统的设计与应用[M].北京:中国电力出版社,2009.
[11]岑可法,倪明江,骆仲泱,等.循环流化床锅炉理论设计与运行[M].北京:中国电力出版社,1998.
[12]王勤辉,骆仲泱,方梦祥,等.循环流化床锅炉炉内流动和燃烧特性的试验研究[J].动力工程,1999,19(3):11-17.Wang Qinhui,Luo Zhongyang,Fang Mengxiang,et al.Characteristics of fluid dynamics and combustion in a circulating fluidized bed boiler furnace-test and research[J].Journal of Power Engineering,1999,19(4):269-274.
[13]仇韬,丁艳军,孔亮,等.CFB锅炉动态特性与负荷和煤质的关系研究[J].中国电机工程学报,2007,27(32):46-51.Qiu Tao,Ding Yanjun,Kong Liang,et al.Research of relationship between CFBB dynamic behavior and power and coal quality[J].Proceedings of the CSEE,2007,27(32):46-51.

