爆破振动信号的提升小波包分解及能量分布特征＊

路 亮，龙 源，谢全民，2，李兴华，纪 冲，赵长啸

（1.解放军理工大学工程兵工程学院，江苏 南京 210007；2.武汉军械士官学校弹药修理与销毁教研室，湖北 武汉 430075）

随着掘进爆破技术在城市隧道开挖中的大力开发和利用，爆破施工对既有相邻隧道结构和设施的安全影响也逐渐成为人们日益关注的问题，其中爆破产生的地震效应是对隧道结构安全最具威胁的危害之一。为最大限度地降低爆破地震效应对结构设施等可能带来的影响，必须解决好对爆破振动特征的认识、结构响应预测和结构破坏或损伤的判定等方面的问题［1－2］，其中，对爆破振动特征的认识是解决爆破地震危害效应的基础，因此，对爆破振动特征的研究具有非常重要的理论和应用价值。

爆破振动本质上是一个非平稳的随机过程，而振动信号经过复杂的岩土介质传播后，往往掺杂着各种频率成分的干扰波，因此，建立在平稳随机过程基础上的傅里叶变换方法无法准确提取和分析信号的振动特征［3］。近年来，小波变换以其良好的时频局部化特性，为爆破振动特征的提取和分析提供了一条有效的途径［4－5］。然而，小波方法由于不能根据振动信号的特点选取适应的小波基来准确识别振动信号特征，致使经典（一代）小波在爆破振动信号的特征提取和分析方面存在局限。

提升算法（lifting scheme）是一种二代小波构造方法，它在继承了经典小波变换多分辨率特性的基础上，通过选择不同的提升算子来改变小波滤波器的特性，得到不同性质的双正交小波，使小波的设计具有更大的灵活性。根据工程应用的需要，通过提升方法可获得具有某种希望特性的小波，从而构造出与信号特性更加匹配的小波滤波器组［6－9］。本文中将以提升算法为基础，依据小波包变换的思想，对信号中的细节分量进一步分解，实现对爆破振动信号的提升小波包 （second generation wavelet packet，SGWP）变换，进而能够准确地提取爆破地震波中不同频带下的振动分量，研究各频带下爆破地震波能量的分布特征，更好地揭示爆炸应力波的传播及衰减规律，为深入研究城市隧道结构在爆破地震效应下的振动响应提供依据。

1 提升算法

提升算法的分解过程可归纳为［8］：

（1）分裂。将信号X 分为偶序列Xe和奇序列Xo。

（2）预测。用相邻的偶序列Xe和预测器P估计信号的奇序列Xo，并将估计误差d作为信号的细节分量，反映了信号中的高频成分

（3）更新。用细节分量d和更新器U，更新偶序列Xe以获得信号的逼近分量c，代表了信号中的低频成分

提升算法的重构过程为分解过程的逆运算，可直接由分解过程得到，重构过程的预测器P和更新器U与分解过程相同。

2 基于提升小波包分解算法的爆破振动信号频带能量表征

2.1 提升小波包分解算法关键技术

2.1.1 小波基的选择

小波基的选择是用小波包方法对信号进行分析时必须要考虑的问题，因为不同的小波基分析同一个信号会产生不同的结果。对爆破振动信号进行小波包分析时，小波基函数的选择一般要遵循具有紧支撑性、对称性和光滑性的原则。

在提升算法框架下，采用插值细分原理［10］设计预测器和更新器，可获得双正交小波的小波函数和尺度函数，一般记这种小波为二代小波（second generation wavelet），记为SGW（N，N～），其中 N、N～分别为小波的预测器和更新器个数。这种小波是对称的、紧支撑的，并且具有冲击衰减形状［8，11］，能较好地与爆破振动信号相匹配，从而可有效抑制变换时振动信号的相位失真。

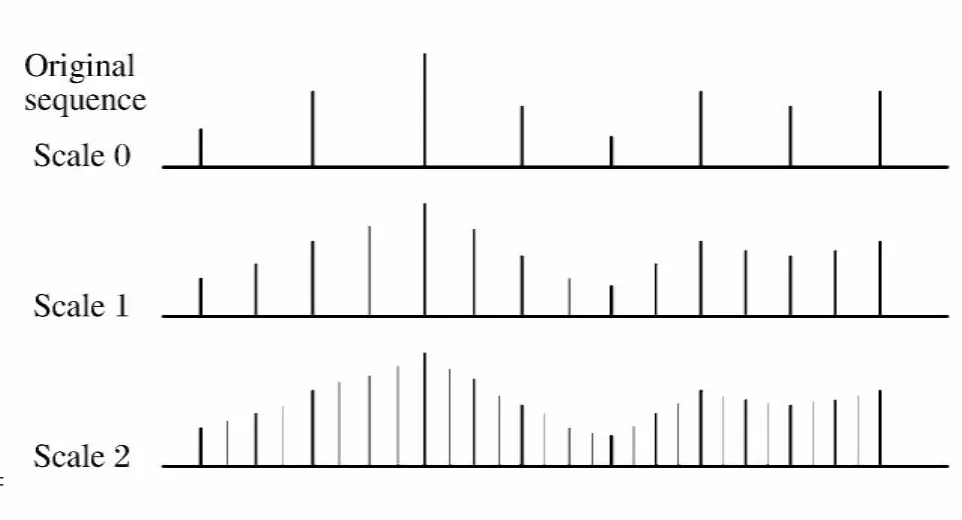
图1 插值细分示意图Fig.1 Sketch of interpolation subdivision

2.1.2 基于插值细分的二代小波的构造

插值细分的本质是在原始样本的基础上采用多项式插值方法来获得新的样本值，即当位于2个相邻样本中间位置的插值点已知时，若插值多项式确定即可求出新的样本值，因此，预测器系数可以通过插值多项式来确定。插值细分示意图如图1所示。

根据Lagrange插值定理［12］，已知N＋1个点x0，x1，…，xN的函数值为y0，y1，…，yN，且 yi＝f（xi），i＝0，…，N，则存在唯一一个次数不大于N的多项式 Ln（x），使得 Ln（xi）＝f（xi），那 么

对于一个已知的插值点x，Ln，i（x）是常数，它与函数值yi无关，插值点x对应的函数值是已知的N＋1个函数值y0，y1，…，yN的线性组合。令Pi＝Ln，i（x），x处对应的函数值为y，则该式说明新的函数值是由已知的一组函数值预测得到的，当x0，x1，…，xN和x确定后，｛Pi｝是唯一的，且∑Pi＝1。

每一次细分时，取 N（N＝2D，D 为正整数）个已知的样本yj，k－D＋1，…，yj，k，…，yj，k＋D，假设这些样本是等时间间隔采样的，它们对应的采样时刻分别为xk＋1，xk＋2，…，xk＋N，其中xk为任意的起始时间，细分产生的新的采样值处于这些已知样本的中间位置。插值点为：x＝xk＋（N＋1）／2，这样预测系数可由式Ln，i（x）确定，即

根据式（3）即可求得几种二代小波的预测器系数，如表1所示。

表1 预测器系数Table1 Predict coefficient of second generation wavelets

文献［9，13］中指出更新器系数为预测器系数的一半，因此，当更新器系数的个数确定后，便可根据预测器的系数来确定更新器的系数。

预测器P和更新器U确定后，分别根据式（1）、（2）经过迭代运算后即可生成尺度函数φ（x）与小波函数φ（x）。图2为经过10次迭代后生成的SGW（6，6）的尺度函数图和小波函数图。

图2 SGW（6，6）的尺度函数与小波函数Fig.2 Scaling function and wavelet function of SGW（6，6）

从图2中可以看出，SGW（6，6）很好地满足了小波基选择必须遵循的原则，具有良好的对称性和紧支撑性，且具有冲击衰减形状。文献［8，11，14］中指出，当 N和较小时，尺度函数和小波函数的支撑区间较小；反之，支撑区间较大。一般支撑区间小的小波函数适合处理非平稳信号，小波系数能够有效地描述信号的瞬态分量，而支撑区间大且连续较好的小波适合于描述稳态信号。因此，本文中将采用SGW（6，6）作为提升小波包变换的小波基。

2.1.3 提升小波包变换的移频算法

小波包分解逐层隔点采样时，采样率会降低1／2。当采样频率低于奈奎斯特（Nyquist）频率时，高频信号会发生频率折叠，对其继续分解会造成频率混叠现象。文献［15－16］中根据混频的原因提出了一种移频算法，其原理为：将高频成分进行移频处理，使其所含的最高频率低于1／2奈奎斯特频率，以避免频率折叠。根据傅里叶变换的移频特性，要使信号x（t）的傅里叶变换x＾（t）频率降低f0，只需将x（t）乘上eiπf0t；设信号的采样频率为fs，则其最高分析频率为fs／2，由于隔点采样，小波包分解到第j层，采样频率将为2－jfs，最高分析频率将为2－j－1fs，则高频小波包分解系数应移频2－j－1fs。

以一段模拟信号为例，信号的波形及时频图如图3所示。选取SGW（6，6），按照提升小波包分解算法，分别采用移频和不移频算法对模拟信号进行2层分解，分解后第2层的节点系数如图4所示。

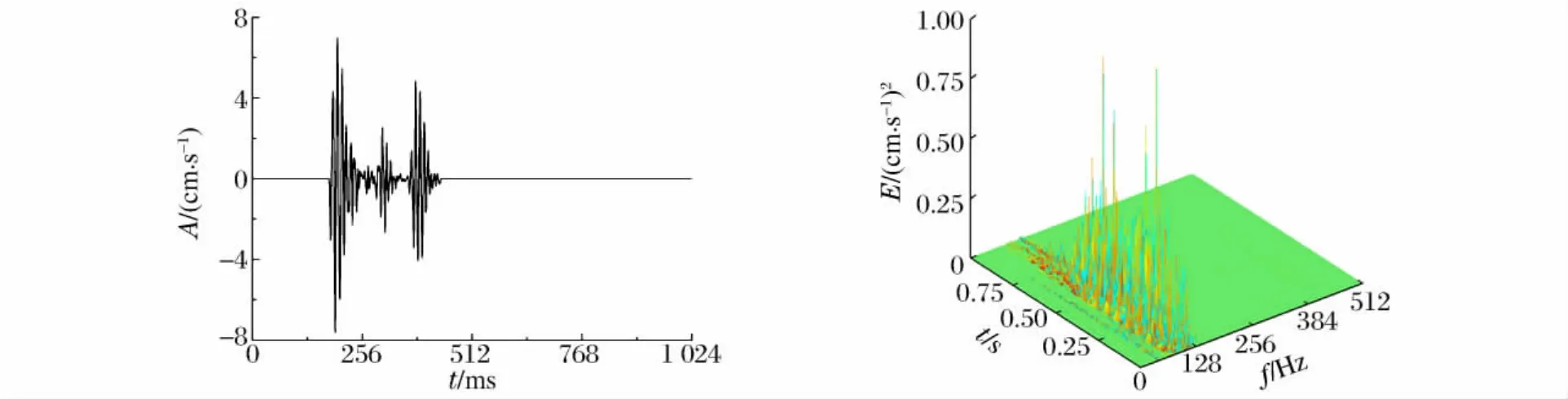
图3 模拟信号波形曲线及三维时频图Fig.3 Wave curve and time－frequency map of simulated signal

由图4可知，两种分解算法得到不同的分解结果，为说明移频算法的合理性，选取（2，0）节点的小波包分解系数进行单支重构，即将其余节点的系数置零，按照提升算法重构过程进行小波包重构。单支重构后的信号如图5（a）所示。

对利用节点（2，0）单支重构后的信号进行短时傅里叶变换［17］，得到如图5（b）所示的时频图。对比后可知，采用移频算法的提升小波包变换可以将原信号按频带精确划分，重构后的信号仅包含0～128Hz的成分；而采用不移频算法重构的信号，由于混频现象致使不能对原信号按频带准确划分，分解结果存在频率失真。

图4 移频与不移频分解结果对比Fig.4 Decomposition results with frequency－shift and no frequency－shift

图5 节点（2，0）单支重构结果Fig.5 The signal－branch reconstruction result of node（2，0）

2.2 爆破振动信号各频带能量表征

信号s经提升小波包i层分解后，可以得到2i个频带上的子空间信号，则s可由这些子空间的正交和表示，即

式中：fi，j为爆破振动信号小波包分解到第i层第j个节点上的重构信号。若s的最低频率为1，最高频率为ω，则第i层每个频带的频率宽度为ω／2i。

根据Parseval定理［18］，由式（4）可得爆破振动信号的能量谱为

式中：m 为爆破振动信号的采样点数，xj，k（j＝0，1，2，…，2i－1，k＝1，2，…，m）为重构信号fi，j的幅值，Ei，j为爆破振动信号分解到第i层第j个节点的频带能量。

由式（5）可知，信号s的总能量为

信号分解到第i层时，各频带能量占总能量的百分比为

由式（4）～（5）可知，爆破振动信号由提升小波包分解成不同频带的振动分量，从而能反映频率在爆破振动时的影响，且频带能量又能同时反映该频带爆破振动分量的强度和作用时间。因此，在此基础上获得的频带能量能同时反映爆破振动信号强度、频率及作用时间的共同作用影响［19］。

3 基于SGWP算法的爆破振动信号能量分布特征

3.1 振动测试

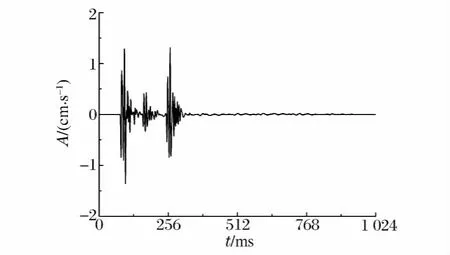
图6 实测振动信号的时程曲线Fig.6 Time－history curve of measured vibration signal

图6为结合某城市隧道开挖工程采集的一段爆破振动波形。本次实验采用EXP－4850型爆破振动测试仪，其最小工作频率为1Hz。因此，仪器的频率响应性能完全满足信号的测量要求。

3.2 爆破振动信号的提升小波包分解

选用2.1.2节构造的SGW（6，6）作为小波基，按照提升算法，对爆破振动实测信号进行5层小波包分解，分解结果见图7。根据式（5）编写计算程序，可将前16节点对应的不同频带内的能量值列于表2中，图8为按照式（6）～（7）求得各频带内的能量百分比分布，通过该图可直观比较振动信号中的能量分布情况。

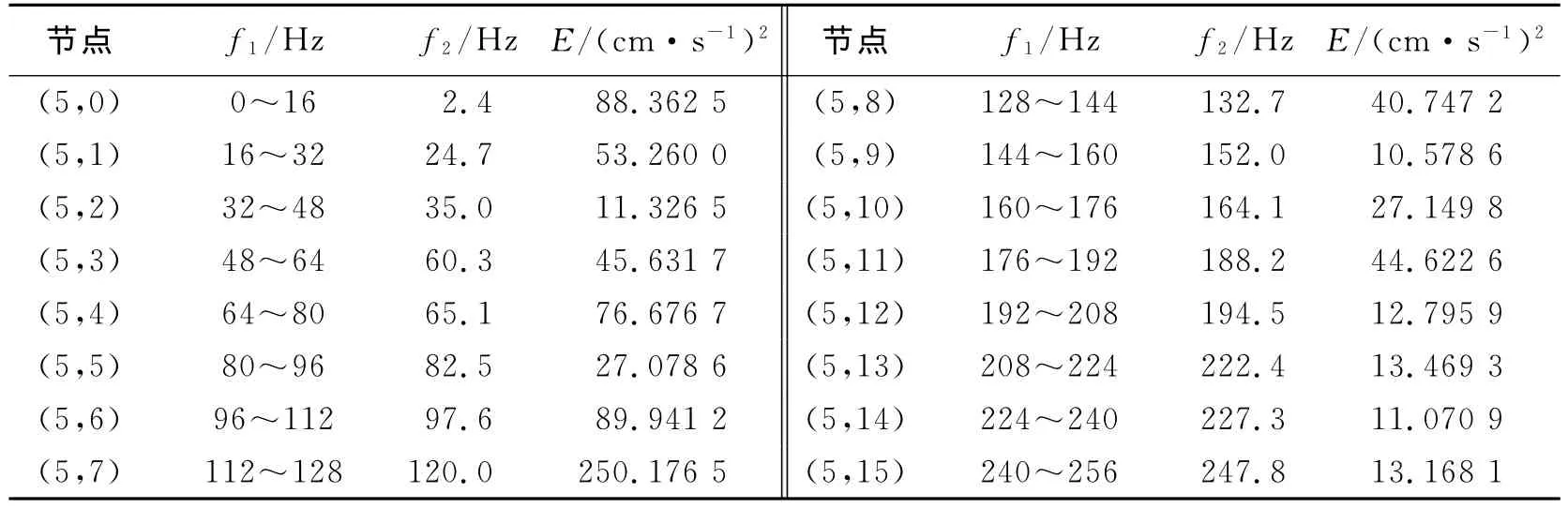
表2 主要频带能量分布表Table2 Energy distribution of main frequency band

图7 提升小波包分解结果Fig.7 Decomposition result of lifting wavelet packet

图8 爆破振动信号不同频带能量百分比分布Fig.8 The percentage of energy for blasting vibration signal in different frequency bands

3.3 爆破振动信号不同频带能量分布规律

从表2、图8中可以看出，信号在0～256Hz间的能量占到总能量的99.4%，表明所选爆破振动信号的能量在频域范围内虽然分布较广，但大多数集中在0～256Hz之间。

信号中频率在256Hz以上的能量在总能量中的所占比例只有0.6%，说明随着雷管段数的增加和振动作用时间的延长，信号中高频成分所占比例减少，能量更加集中在主振频带附近。

（3）通过表2可知，信号在其频域中除含有一个主振频带外，还存在多个子频带，子频带中又有各自主频且能量分布很不均匀，直接反映在爆破振动信号中出现多个峰值。由此可见，在爆破振动安全判据中，只参考单个主振频率有欠准确，而应将多主频的影响考虑进去。

图9 重构信号与实测信号的相对误差Fig.9 Relative error of reconstruction and measurement signal

3.4 SGWP算法有效性检验

依据SGWP分解算法逆运算对图8中的各节点系数进行信号重构，得到重构信号与实测信号的相对误差ε如图9所示。从中可以看出，重构信号与实测信号的误差ε量级均在10－6以上，对工程分析、计算的影响可忽略不计。因此，本文中用SGWP算法对爆破振动信号进行信号分解的过程中，信号的能量损失可忽略不计，因此本文中所用的分析方法是有效的，可以保证真实反应爆破振动信号中的能量分布情况。

4 结 论

（1）根据小波包变换具有多分辨率分析的优点，通过设计基于插值细分的二代提升小波基，实现对爆破振动信号的提升小波包分解，较好地解决了变换时振动信号的相位失真；

（2）针对信号经小波包分解采样率会降低的特点，通过引入移频算法，有效避免了采样频率低于Nyquist频率时，高频信号频率发生折叠造成的频率混叠现象，通过模拟信号的单支重构证明了移频算法的合理性；

（3）依据提升小波包分解算法，通过将爆破振动信号分解到不同频带上，可以对不同频率范围内振动分量的时间变化规律加以分析，以给出爆破振动信号的时－频分布特征，为爆破振动研究提供了新的分析手段；

（4）实测信号的能量特征研究表明，基于提升小波包算法的能量特征分析方法可以很好地与爆破振动等非平稳信号相匹配，不仅能准确地了解爆破振动信号的能量－频率分布，还可以给出不同频带上的振动分量分布和时间衰减规律，为指导结构抗震设计和工程爆破监测提供分析依据。

［1］Dowding C H.Blasting vibration monitoring and control［M］.Englewood Cliffs：Prentice－Hall，1985：1－5.

［2］晏俊伟，龙源，方向，等.基于小波变换的爆破振动信号能量分布特征分析［J］.爆炸与冲击，2007，27（5）：405－409.Yan Jun－wei，Long Yuan，Fang Xiang，et al.Analysis on features of energy distribution for blasting seismic wave based on wavelet transform［J］.Explosion and Shock Waves，2007，27（5）：405－409.

［3］何军，于亚伦，梁文基.爆破振动信号的小波分析［J］.岩土工程学报，1998，20（1）：47－50.He Jun，Yu Ya－lun，Liang Wen－ji.Wavelet analysis for blasting seismic signals［J］.Chinese Journal of Geotechnical Engineering，1998，20（1）：47－50.

［4］谢全民，龙源，钟明寿，等.基于小波、小波包两种方法的爆破振动信号对比分析［J］.工程爆破，2009，15（1）：5－9.Xie Quan－min，Long Yuan，Zhong Ming－shou，et al.Comparative analysis of blasting vibration signal based on wavelet and wavelet packets transform［J］.Engineering Blasting，2009，15（1）：5－9.

［5］张耀平，曹平，高赛红.爆破振动信号的小波包分解及各频段的能量分布特征［J］.金属矿山，2007（11）：42－43.Zhang Yao－ping，Cao Ping，Gao Sai－hong.Wavelet packet decomposition of blasting vibration signals and energy distribution characteristics of frequency bands［J］.Metal Mine，2007（11）：42－43.

［6］张德丰.MATLAB小波分析［M］.北京：机械工业出版社，2009.

［7］姜洪开，何正嘉，段晨东，等.基于提升方法的小波构造及早期故障特征提取［J］.西安交通大学学报，2005，39（5）：494－498.Jiang Hong－kai，He Zheng－jia，Duan Chen－dong，et al.Wavelet construction based on lifting scheme and incipient fault feature extraction［J］.Journal of Xi’an Jiaotong University，2005，39（5）：494－498.

［8］Sweldens W.The lifting scheme：A construction of second generation wavelet［J］.SIAM Journal on Mathematics Analysis，1997，29（2）：511－546.

［9］Claypoole R L，Davis G M，Sweldens W，et al.Nonlinear wavelet transforms for image coding via lifting［J］.IEEE Transactions on Image Processing，2003，12（12）：1449－1458.

［10］Daubechies I，Sweldens W.Factoring wavelet transforms into lifting steps［J］.Journal of Fourier Analysis and Application，1998，4（3）：247－269.

［11］段晨东，张建丁.基于第二代小波变换的转子碰摩故障特征提取方法研究［J］.机械科学与技术，2006，25（10）：1229－1232.Duan Chen－dong，Zhang Jian－ding.Study of the fault feature extraction method for rotor rub－impact based on the second generation wavelet transform［J］.Mechanical Science and Technology，2006，25（10）：1229－1232.

［12］邓建中，刘之行.计算方法［M］.2版.西安：西安交通大学出版社，2001.

［13］Sweldens W，Schröder P.Building your own wavelets at home［DB／OL］.http：／／cm.bell－labs.com／who／wim／papes.html／at home，1998－01－05.

［14］Sweldens W.The lifting scheme：A custom－design construction of biorthogonal wavelets［J］.Applied and Computational Harmonic Analysis，1996，15（3）：186－200.

［15］耿中行，屈梁生.小波包的移频算法与振动信号处理［J］.振动工程学报，1996，19（2）：145－152.Geng Zhong－xing，Qu Liang－sheng.Frequency shift algorithms of wavelet packet and vibration signal analysis［J］.Journal of Vibration Engineering，1996，19（2）：145－152.

［16］刘世元，杜润生，杨叔子.小波包改进算法及其在柴油机振动诊断中的应用［J］.内燃机学报，2000，18（1）：11－16.Liu Shi－yuan，Du Run－sheng，Yang Shu－zi.An improved algorithm for wavelet packets and its applications to vibration diagnosis in diesel engines［J］.Transaction of CSICE，2000，18（1）：11－16.

［17］Alan V O，Ronald W S，John R B.Discrete－time signal processing［M］.刘树堂，黄建国，译.西安：西安交通大学出版社，2001：557－582.

［18］周德廉，邵国友.现代测试技术与信号分析［M］.徐州：中国矿业大学出版社，2005.

［19］中国生，熊正明.基于小波包能量谱的建（构）筑物爆破地震安全评估［J］.岩土力学，2010，31（5）：1522－1528.Zhong Guo－sheng，Xiong Zheng－ming.Safety assessment of structure by blasting seism based on wavelet packet energy spectra［J］.Rock and Soil Mechanics，2010，31（5）：1522－1528.