一种新的应用变精度粗糙集的决策树构造方法
王 越,万 洪
(重庆理工大学计算机科学与工程学院,重庆 400054)
决策树是一种比较常见的分类分析方法,具有效率高、知识的表达和规则的提取易于理解等特点,已得到广泛的应用。目前,构造决策树的方法有很多,其中 Quinlan[1-2]于 1986 年提出的 ID3算法和C4.5算法是最经典的。这两种算法的主要思想是:在各非叶子节点选择信息增益最大的属性(属性组合),自顶向下地划分训练实例集,直到满足无可分样本、无剩余属性或样本同属于一个类别等终止条件。但这些方法面临的主要问题有:倾向于选择取值较多的属性,抗噪声能力差,一棵决策树中子树有重复,以及有些属性在一棵决策树中的某一路径上被多次检验,从而降低了分类的效率和效果[1]。
Z.Pawlak教授[3]于 1982 年提出粗糙集理论(rough set)[3],从另一角度认识知识,把论域的分类看作是知识,从而能非常严谨地对知识进行理解。粗糙集理论对问题的处理方式独特,不需要确定某些问题中的数量,而是从问题本身出发,这给决策树的构建带来了便利。在信息处理、数据挖掘等认知领域该理论已得到广泛应用[4]。可变精度粗糙集[5](variable precision rough set,VPRS)理论是Ziarko在Z.Pawlak粗糙集模型的基础上,通过设定误差阈值参数β(0.5≤β<1),在一定程度上放宽了对不可分辨关系的要求,使泛化能力和抗噪声能力有很大的改进。当β=1时,变精度粗糙集就变成了Z.Pawlak粗糙集。ID3算法被提出以来,对此算法的改进与研究已十分广泛。文献[6-8]均在原有算法上利用粗糙集理论进行了各种改进,这些方法中大部分以分类精度、属性重要性、属性依赖度以及正域等度量标准作为条件属性的选择条件,并取得了较好的效果。然而,这些改进算法有些侧重于属性某一时刻的分类能力,没有把属性间的关系考虑在内;有些则侧重于属性的整体分类效果,忽略了属性的某一时刻的分类能力,导致最终难以达到全局最优的分类效果。
本文将属性的当前分类能力和属性间的关联度综合在一起,提出变精度决策分类熵和信息决策熵的概念,并以信息决策熵作为决策树属性选择的标准;将属性当前分类能力和协调性相结合,通过调节误差阈值参数β,有效地抑制了训练数据中的噪声数据带来的干扰,并允许在构造决策树的过程中划入正区的实例类别存在一定的不一致性,简化生成的决策树,提高决策树的泛化能力。理论分析和实验结果表明:与经典的ID3决策树算法和文献[6]中的算法相比,该算法能得到简洁、高效的决策树。
1 基于变精度粗糙集的信息决策熵
1.1 粗糙集的相关概念
粗糙集的基本概念和理论参见文献[3-4],本文仅介绍涉及到的基本概念。
定义1 决策系统[3]
一个决策系统 S={ U,A,V,f}为一个有序的四元组,其中:U={x1,x2,…,xn}为论域,是所有对象{x1,x2,…,xn}的有限集合;A是属性的有限集合,A=C∪D,C为条件属性集,D为决策属性集,且C∩D=Φ;V=是属性值的集合,Va是属性a的值域;f:U×A→V是一个信息函数,表示任意对象xi的属性在V上的取值。该系统又称为信息系统。
定义2 不可分辨关系[3]和协调度[3]
设决策系统 S={ U,A,V,f},其中 A=C∪D,C为条件属性集,D为决策属性集。设B是属性集合的一个子集,B在U上产生的一个不可分辨关系:IND(B)={(x,y)∈U × U:f(x,a)=f(y,a),∀a∈Β},它表示对象x和y关于属性集A的子集B是不可区分的。
对于∀d∈D,B⇒b的协调度为
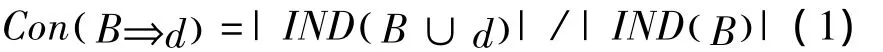
定义3 下近似和上近似[4]
设一个子集为X,对象a的论域为U,其中U的一个等价关系为R,则所有与a不可分辨的对象所组成的集合可表示为[a]R,即由a决定的等价类。当集合能表示成基本等价类组成的并集时,则称集合是可以精确定义的;否则,集合只能通过近似的方式来刻画。集合X关于R的下近似定义为
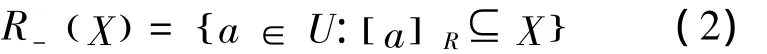
实际上,R-(X)表示的是由某些已有的条件判断某个对象肯定属于集合X的所组成的最大的对象的集合,也称为X的正域,记作POSR(X)。相反,判断肯定不属于集合X的对象组成的集合称为X的负域,记作NEGR(X)。集合X关于R的上近似定义为
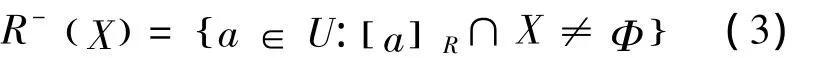
从表达式可以看出,R-(X)是[a]R与X相交时所有非空的等价类的并集,是某些对象可能属于X时所组成的最小集合。
定义4 给定决策系统 S={ U,A,V,f},A=C∪D,C为条件属性集,D为决策属性集,对于每个子集和等价关系 R,U/R={y1,y2,…,yn},则X的β-下近似和β-上近似可定义为[9]:
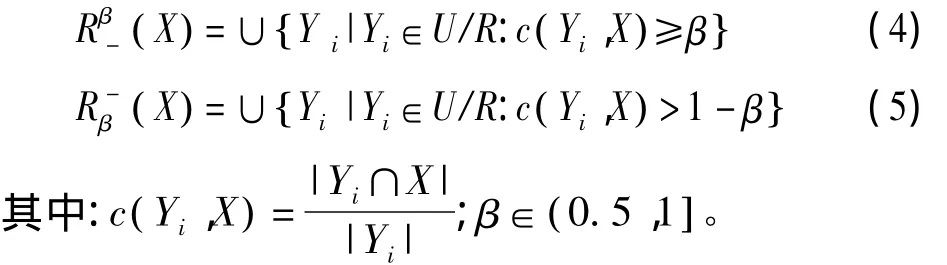
1.2 变精度决策分类熵
定义5 给定决策系统 S= U,A,V,(f),其中A=C∪D,C为条件属性集,D为决策属性集。对于每个条件属性Ci∈C,定义式(6)为变精度正目标分类比例(||为基数,即集合中元素的个数)。
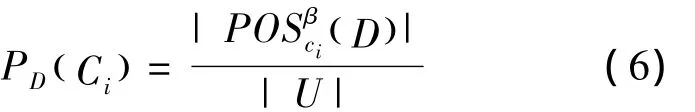
定义式(7)为变精度负目标分类比例。
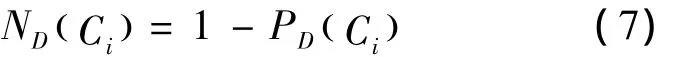
定义式(8)为Ci相对于D的变精度决策分类熵。
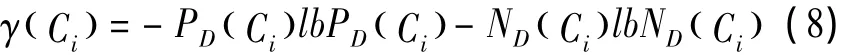
γ( Ci)与ID3算法中的信息熵的形式相类似,代表条件属性分类能力的强度,由于精度因子β的存在,故称其为属性Ci相对于决策属性D的变精度决策分类熵,简称属性Ci的变精度决策分类熵。
1.3 属性选择标准——信息决策熵
由以上分析可得:变精度决策分类熵是条件属性相对于目标分类的分类能力的度量。在基于变精度决策分类熵进行分类时,其分类思想是:希望能先识别出一部分对象,每次尽量减少分类对象的数量,并且通过调节精度因子β来提高决策树的泛化能力。变精度决策分类熵也能在构造决策树时简化算法,因为它不需要考查属性的每一种可能的取值,同时它以目标分类作为参照,可以对属性的选择范围进行约束,减少了算法的运行时间,同时选择分类能力高的属性可以构建优越的决策树。但是令人遗憾的是,此方法没有考虑属性间的依赖关系和当前属性对将来分类的影响,仅仅是将属性的当前分类能力作为属性的选择标准。为了更好地优化算法,把属性之间的协调度考虑进来,将两者相结合得到属性选择依据的新指标——属性 B的信息决策熵(information decision entropy,IDE)。考虑单变量决策树情况,B={ Ci},Ci∈C,则有
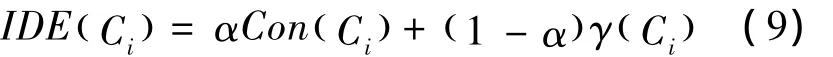
式(9)中α是权重系数,用来调节属性选择的侧重性,是IDE( Ci)属性选择要求的综合体现。α的值对分类的结果是有影响的,但是为了达到预期要求,可以根据分类效果来调整 α的取值。由IDE( Ci)的定义可知,IDE(Ci)的取值范围是[0,1]。因此,IDE( Ci)的值越大,属性集中的对象属于同一类别的概率就越大,IDE( Ci)的值为1表示每个属性集中的对象属性为同一类别。
2 基于信息决策熵的决策树构造算法(IDEDT)
2.1 数据预处理
连续属性离散化:连续的属性只有经过离散化后才能应用在粗糙集理论中。目前,有关连续属性的离散化已有多种方法,如基于动态层次聚类离散化[10]、基于信息熵[11]等。
条件属性约简:为使空间降维,属性必须经过约简处理。目前关于属性(知识)的约简也有多种方法,如基于可辨识矩阵的约简[12]、基于互信息的约简[13]、基于二进制区分矩阵的约简[14]等。
2.2 决策树的构造
把信息决策熵作为属性选择依据来进行决策树构建的基本思想是:首先根据计算选择最佳的条件属性,特殊情况下,当精度因子β取某一值时,某条件属性的变精度正目标分类比例为0,此时,此属性的变精度决策分类熵计算没有意义。这种情况下,令其信息决策熵等于属性协调度,并将其作为属性选择的标准。当所有条件属性的变精度正目标分类比例均为0时,调节精度因子β重新计算。当某条件属性的变精度正目标分类比例为1时,优先选择此属性作为测试属性,不再计算其他属性的信息决策熵,以提高算法运行效率。计算出最佳属性计算之后,用此属性作为依据去构造决策树,该属性的值的个数决定决策树的分支数。之后,再在每一个分支中用同样的方法选择划分属性。同时,为避免决策树中属性的重复选取,在属性集合中将选择过的属性删除。当决策树的某一分支中的所有对象都属于一个决策类时,就把该分支设为叶结点,结点名为该决策类名,算法直到树中所有的分支都到达叶结点时结束。
现将本文提出的基于信息决策熵的决策树构造的算法描述如下:
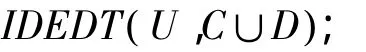
输入:决策系统 S={ U,A,V,f},A=C∪D,C为条件属性集,D为决策属性集,精度因子β,权重系数α。
输出:单变量决策树T。
算法步骤:
步骤1 初始化,对决策系统S进行约简,其中的一个约简记为:S'=(U',C'∪D)。
步骤2 构造一个根节点为N(M,C)的树,其中M和C分别为全体样本集和全体属性集。
步骤3 IF U'为空,则返回。
步骤4 IF U'中的全部样本都属于同一类C,则返回N为叶节点,并标记为类C。
步骤5 IF C'为空,则返回N为叶节点,标记N中出现最多的类。
步骤6 对 C'中的每一个条件属性a∈C',做以下操作:
1)根据a和决策属性D,得到对U'的初始划分模式(等价类);
2)根据划分模式,计算a与决策属性D之间的协调度;
3)计算a的决策分类熵;
4)计算a的信息决策熵IDE( a)。
步骤7 选择信息决策熵最大的属性作为测试属性,假设测试属性为a,根据a的不同取值将U'分为V个不相交的子集 U'j(j=1,2,…,v)。在每个子集中构成一个分支,随后从条件属性集中删除选取过的属性a,即C'=C'-a;当所有条件属性的信息决策熵均为0时,调节精度因子β,重复步骤6。
步骤8 对于每个分支,递归的调用IDEDT( Uj,C'∪D)。
步骤9 返回。
3 实例分析
下面采用文献[6]中的决策系统作为数据源,分别同文献[6,8]中提出的算法进行比较。决策系统如表1所示。
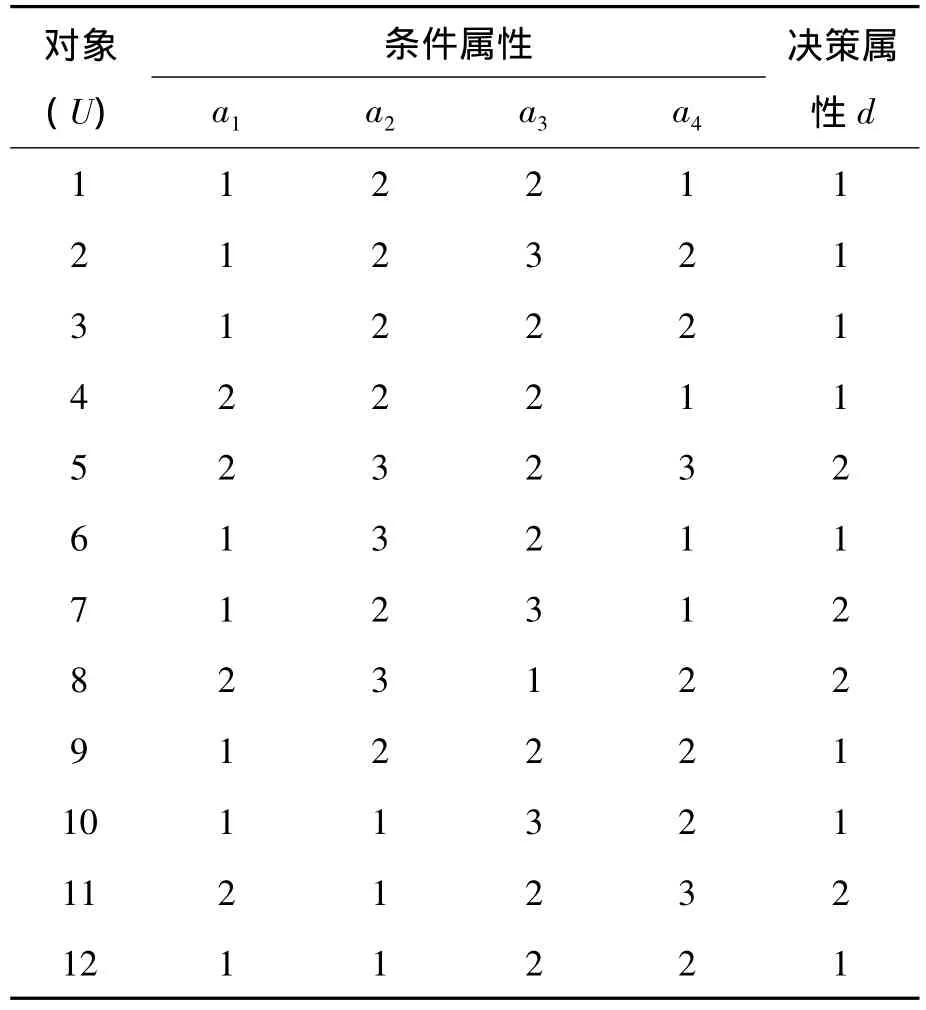
表1 决策系统
为了方便和其他2种算法进行比较,决策系统没有进行约简,其中:论域 U={1,2,3,…,12};条件属性 C={a1,a2,a3,a4};决策属性 d={1,2}。取 β=0.8,α=0.3,IDEDT 方法构造决策树的过程如下(只计算a1的信息决策熵):


根据算法,取最大的信息决策熵作为测试属性,故选a1。填充当前节点构建子节点并判断它们是否满足终止条件,发现当a1等于1时,论域中只有一个对象不能被正确分类,其精确度为7/8=0.875>0.8。因此,可以认为a1等于1时满足终止条件。a1=2时不满足终止条件,则对它们分别递归调用构建算法。最后建立的决策树如图1所示。
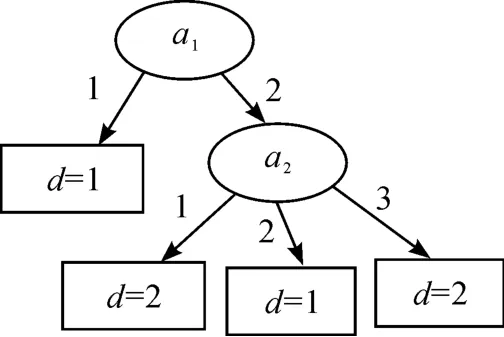
图1 IDEDT算法构造的决策树
图1是基于本文提出的IDEDT算法构造的决策树。从图1可以看到:决策树的复杂性(树中所有节点的个数)为6,叶节点数为4,对应规则为4条。图2是文献[8]中提出的算法构造的决策树,其复杂性和节点个数和本文算法一样。图3是利用文献[6]中的算法构造的决策树,决策树的复杂性为8,叶节点数为5,对应规则为5条。图4是基于信息熵的算法构造的决策树,决策树的复杂性为12,叶节点数为7,对应规则为7条。可以发现,本文中的算法以及文献[6]和文献[8]中的算法相比原始的基于信息熵的ID3算法都有一定的改进。然而本文算法和文献[8]中的算法在本实例中构造的决策树的复杂性相差不大,而且本文算法的计算还相对复杂。在实验部分把这4种算法在不同的数据集中进行比较,可以发现:本文中的IDEDT算法相比其他算法而言,它构造出的决策树在深度、规模、规则、长度等方面都有明显的优势。主要原因在于本文算法中的属性选择标准信息决策熵综合考虑了条件属性的当前分类能力和条件属性与决策属性之间的依赖度,而且算法中的精度因子使决策树的泛化能力有很大的提高。为了避免属性的重复选取,将选取过的条件属性从属性集中删除,从而使生成的决策树规模小而分类能力强。
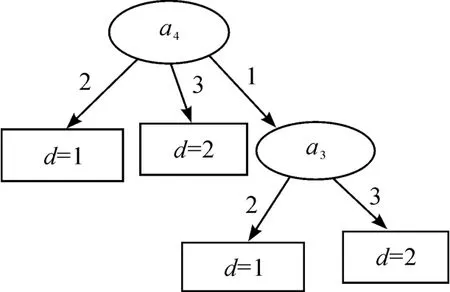
图2 文献[8]中算法构造的决策树
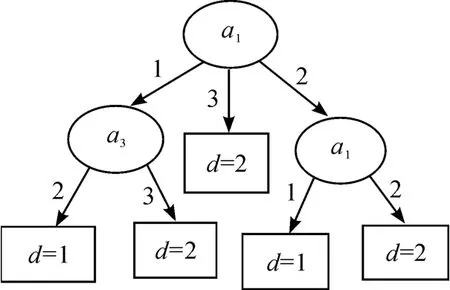
图3 文献[6]中算法构造的决策树
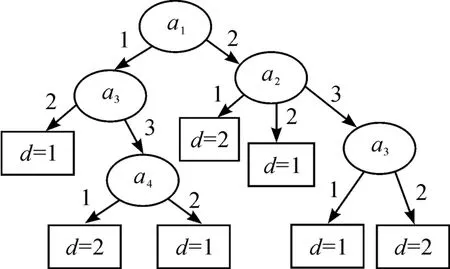
图4 ID3算法构造的决策树
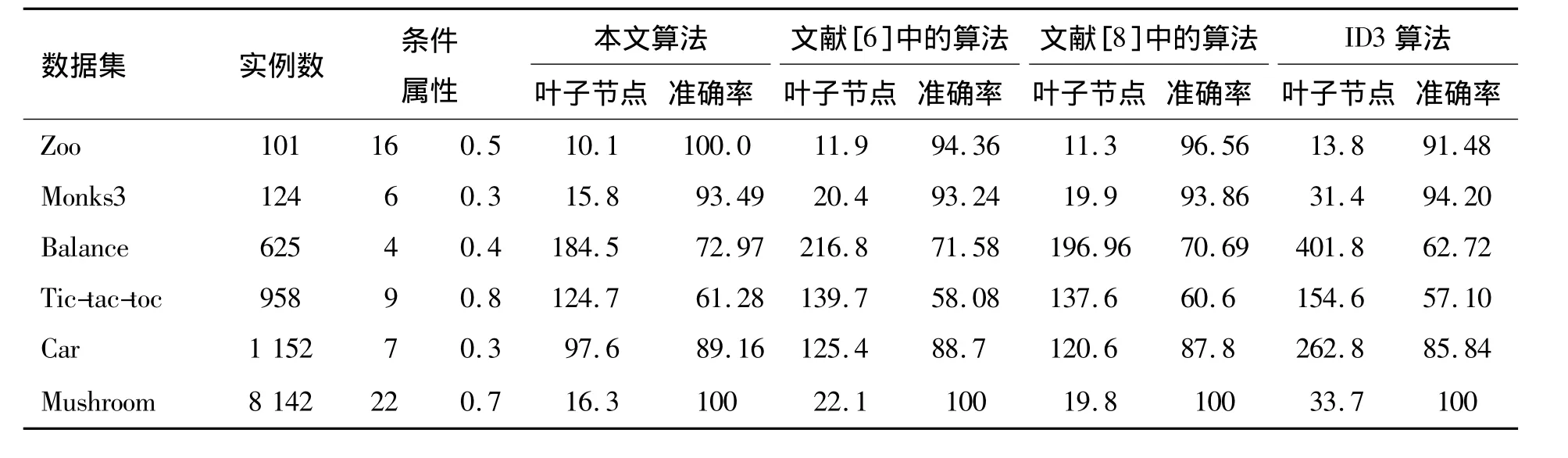
表2 不同算法生成的决策树的比较(准确率/%)
4 实验结果
为了测试算法的性能,本文在UCI[16]提供的部分数据集上分别运行了IDEDT算法、文献[6]中的算法、文献[8]中的算法和传统的基于信息熵的ID3算法,所选的数据集都经过了数据的预处理。用10层交叉的方法测试3种方法构造的决策树的平均分类精确度,对于没有测试集的数据集按照2∶1的比例划分成相应的训练集和测试集。同时为了更好地对这3种算法进行比较,随机抽取每一个数据集,把它分为10个不同的子集;然后,用上述4种算法分别在数据子集上进行决策树的构造;最后对平均叶子节点数进行统计,并且在不同的算法参数α设置下进行实验计算,确定合适的算法参数取值。得到的结果如表2所示。没有特别说明时,实验中取 β=0.8。
从表2可以看出,与基于信息熵的ID3方法和文献中的算法相比较,基于信息决策熵的方法有较高的平均分类精确度,同时构造的决策树有较低的复杂性。
作为一种分类算法,分类的准确率和从树中导出的规则的简洁程度都是衡量决策树性能优越性的一种重要指标,规模越小的决策树产生的规则越简洁,有利于规则的理解和使用。由于IDEDT算法并不是对所有训练数据进行精确匹配,而是还考虑了条件属性的当前分类能力和条件属性与决策属性之间的依赖度,因而,同ID3算法、文献[6]的算法以及文献[8]中的算法相比,构建的决策树规模大幅度降低。同时也说明本文算法相对于文献[8]中的算法,在处理大的数据集时有更好的效果。
5 结束语
本文在变精度粗糙集理论基础上进行分析,引出了信息决策熵的概念,并将其应用于决策树的构建。信息决策熵综合考虑条件属性的当前分类能力和条件属性与决策属性之间的依赖度。实例分析实验证明。本文的算法是有效的,但对于IDEDT算法暂且只能处理离散型的数据,下一步工作将是对算法进行修改使其能处理连续型的数据。另外,IDEDT算法中的两个参数α和β对算法的分类精度的影响与数据集中数据的具体分布有关,寻求最佳的α和β以提高算法的性能将是下一步的工作重点。
[1]Quinlan J R.Induction of Decision Trees[J].Machine Learning,1986,1(1):81 -106.
[2]Quinlan J R.C4.5:Programs for Machine Learning[M].San Mateo,CA:Morgan Kaufmann,1993.
[3]Pawlak Z.Rough Sets[J].International Journal of Computer Information Science,1982,11(5):341 -356.
[4]韦萍萍.结合ROUGH集的决策树构建方法[J].重庆工学院学报:自然科学版,2007,21(8):101-103.
[5]Ziarko W.Variable precision rough set model[J].Journal of Computer and System Sciences,1993,46(1):39 -59.
[6]董广,王兴起.基于决策分类熵的决策树构造算法及应用[J].计算机应用,2009,29(11):3104 -3016.
[7]蒋芸,李战怀,张强,等.一种基于粗糙集构造决策树的新方法[J].计算机应用,2010,24(8):21 -23.
[8]常志玲,周庆敏.基于变精度粗糙集的决策树优化算法研究[J].计算机工程与设计,2006,27(17):3175-3177.
[9]庞哈利,高政威,左军伟,等.基于变精度粗糙集的分类决策树构造方法[J].系统工程与电子技术,2008,30(11):2161-2163.
[10]苗夺谦.Rough Set理论中连续属性的离散化方法[J].自动化学报,2009,27(3):296 -302.
[11]Han jiawei,Kamber M.数据挖掘概念与技术[M].北京:机械工业出版社,2001.
[12]常犁云,王国胤,吴渝.一种基于Rough set理论的属性约简及规则提取方法[J].软件学报,2009,10(11):1206-1211.
[13]苗夺谦,胡桂荣.知识约简的一种启发式算法[J].计算机研究与发展,2010,36(6):681 -684.
[14]杨萍,李济生,黄永宣.一种基于二进制区分矩阵的属性约简算法[J].信息与控制,2010,38(1):70 -74.
[15]Blake C,Merz C J.UCI repository of machine learning databases[EB/OL].[2002 -09 -20].http://www.ics.uci.edu/~ mlearn/MLRepository.

