基于云计算及数据挖掘技术的海量数据处理研究
王鹏,王健安,郭畅,巴济慈
(长春理工大学 计算机科学技术学院,长春 130022)
随着网络技术的飞速发展,存储于计算机中的数据文件呈爆炸式的发展。这些数据又称为海量数据,这类数据常常伴随着噪声而且是异构数据,其很难直接被用户理解。如何从这样的数据里提取出规律和模式已经成为一个难题。数据挖掘作为一门能够高效的、便于扩展的解决以上问题的技术应运而生。选择云计算做海量数据的分类数据挖掘处理,可以减少构建分布式计算平台的开销,同时将底层屏蔽掉,便于开发,使得原有的设备拥有对大数据集的较高处理效率,增加了节点的个数和容错能力,提高了从海量数据中提取有效信息的能力[1,2]。
1 SPRINT算法
SPRINT算法主要包括树的创建与剪枝过程,由于在创建决策树时要求数次遍历数据,但剪枝却不需此过程,所以,对树的剪枝时间基本仅有创建数的百分之一。因此,我们把重点放在树的创建上;另外一方面,基于二叉树简洁又精准的特点,本文选择的是创建二叉树。
1.1 数据结构
SPRINT算法表示数据特征的方式是采用属性表与直方图这两种数据结构,其中,后者是依附在前者之上,而前者又是随着节点的划分而分裂的。它会依据属性的不同性质,如连续型或离散型而显现出相应的表现形式。
属性表是属性值,类标记和记录索引构成的三元组,它可以驻留在除内存外的介质上。直方图是表示节点上的一个属性所属类的分布情况,当属性是连续的数值型时,节点就涉及两个直方图:Cbelow表示已经处理完毕的样本的类型分布,而Cabove表示尚没处理的样本,它们通过不间断的刷新来找到最佳分裂点;当属性是离散型时,便仅需一个直方图,包括了这个属性每个值的类分布信息,只需要维护一个叫做计数矩阵的统计图。
1.2 最佳分裂点的度量和选择
SPRINT算法使用Gini指数代替信息量作为选择最佳分裂点的依据,它对决策树的生成至关重要,Gini指数方法可以定义为[3]:
对有着M个类型的N项记录的数据集S,对应的Gini为:
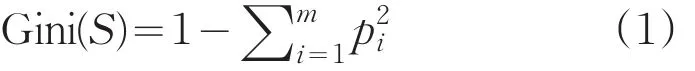
pi为第i类数据出现的频率。
对数据集S划分为S1、S2两个部分,分别有n1、n2个记录,则对应的Gini指数定义为:

处理属性的类型不相同的属性,采差别化的方法:如果是连续的数值型属性P,经过排序后,设其结果为<p1,p2,…,pn>,由于分裂只会发生在相邻节点之间,故有n-1个选择,分裂的形式是P≤pi与P>pi这两个部分,这是就选择相邻两值的中间值即(pi+pi+1)/2为待选的最佳分裂点。从小到大依次扫描,为每个待选的分裂点生成属性表的直方图,并计算它们的基尼值,取最小点为最佳分裂点;而如果是离散型的属性Q,就假设有n个不一样的取值。要做的工作就是把这些值组合为两个集合,即存在2m个选择。算出所有的基尼指数,选用指数最小的为最佳分裂点。
1.3 SPRINT算法基本思想
传统的SPRINT算法过程为:
(1)把数据集S做竖直的分割,之后生成属性表,它们表示着这个数据集全部的特征。若属性为连续型,就要进行排序处理了。
(2)创建一个根节点M,并把全部属性表附着在上面。
(3)对 M 执行BuildTree(S,A)。
(4)决策树创建完毕后,就要对树做剪枝处理了。最常用的方法是最小描述长度。由于树的剪枝仅占SPRINT算法的执行时间的一部分,所以在验证算法有效性的时候将忽略剪枝的时间复杂度[4]。
2 SPRINT算法并行策略
2.1 节点之间的并行
传统SPRINT算法的核心在于数据集的分裂,属性表依附于节点之上,当它发现了核实的分裂点便进行分裂。分裂之后继续在新的节点上进行分类。而在SPRINT并行算法中,通过调用Map函数接受一组键值对,之后将输出的中间健值对发送到Reduce函数。基于以上特性,算法就能够用Map函数将在同一个树层节点的全部的属性表发送到不一样的Reduce中去从而实现分裂的并行,如图1所示。

图1 节点之间的并行
2.2 属性表之间的并行
SPRINT算法在处理属性表时需要各自求出Gini指数并对最佳分裂点进行处理,这些操作都符合并行特征,可以采取并行的处理方式。但是由于进行操作的节点的属性表必须是有着一样的属性名称,所以,属性表之间的并行还需要在节点并行的策略基础之上才能实现,而且全部的属性表均标记上它所依附的节点的特定符号。

图2 属性表之间的并行
因此,若想要使得属性名不一样或是节点符号不一样的属性表可以并行处理如图2仅需在执行Map函数的过程中将分区函数Partitioner规定为:仅当属性表的节点符号一样并且属性表的属性也相同时才可能将它们映射到同一个Reducer。
2.3 排序的并行
在进行连续型属性的分裂之前,需要算出基尼指数和选择候选最佳分裂点,所以一定要预先进行排序。如果属性是连续型的,需要这两个直方图Cbelow和Cabove,分别代表未被扫描和已扫描过的属性表。连续型的属性的直方图的扫描过程为:一边对已排好序的属性进行扫描一边做刷新处理,把扫描的每一个节点都视为待选最佳分裂点进行处理,同时算出它的Gini指数。这样结束扫描时,就将Gini指数最小的待选最佳分裂点选作最终分裂点。
3 并行SPRINT算法到HADOOP平台的移植
3.1 并行SPRINT算法详细设计
并行的SPRINT算法相比于传统的SPRINT算法,除了需要具备属性表和直方图这两类数据结构之外,还需要引入哈希表来存储每次节点分裂之后的子节点的数据信息。通过这些记录的子节点信息来为节点的并行分割提供依据。其中哈希表的数据结构包含两类信息:一是决策时的节点号,用Tree-NodeID表示;另一个是当前树节点的子节点号,用ChildNodeID表示。ChildNodeID的值包括0和1,0代表该树节点是左子节点,1代表该节点是该树节点的右子节点。
其中计算最佳分裂点的部分代码如下所示:


3.2 SPRINT并行算法的移植
SPRINT并行算法的移植的过程主要是完成其算法的MapReduce化,通过Map()和Reduce()两个函数实现。这两个函数算法N-S图如图3和图4所示。

图3 Map函数N-S图

图4 Reduce函数N-S图
在上述处理结束后,属性表就已全部分送到了对应的叶子节点上了。此时,已经结束了整个决策树的创建。当前节点的有关文件存放到了分布式文件系统。具体的表示方法如表1所示,其中,不论是叶子节点与非叶子节点都用N代表。“fleaf”代表这不是叶子节点,而“tleaf”代表这是叶子节点。

表1 节点信息到HDFS的保存格式
采用了这样的表示方法,就能够方便的从HDFS中提取到简单易懂的决策树结构。所以本阶段的主要工作就是从保存在HDFS中的上一阶段的Reduce输出中得到整颗树的构造情况。
4 实验结果
本实验使用一个驾车风险高低预测的公用数据集作为训练集,它记录的是参保车险的车主的一些信息。其中图5为创建的决策树中全部节点信息,0、1代表风险的高低,P1至P4分别代表的是车主的年龄,性别,车种以及受教育程度。

图5 决策树中全部节点信息
为了判断算法挖掘产生出的模式是否正确,在实际操作的过程中,就是把将全部的样本集分割成了五个没有交集的组,去测试准确率。由此得到的数据如表2所示。
从表2可以计算出算法的准确率E为76.2%。
通过计算我们可以发现算法的预测结果的准确率在能够接受的范围之内。为了达到测试算法的伸缩性的目的,本文的实验对一千万条数据做了运行时间的评价。分别用三次实验构建了有着一至三个节点的集群。通过测试这些节点数量递增的集群,得到了如表3所示的对算法的一个循环单元的执行时间信息。

表3 不同节点数的算法执行时间
通过观察上表不难发现,在集群里每添加一个节点,算法的执行时间都会显著下降。这表明增加节点的个数可以提高并行度,继而提高算法效率。而这一切均可以证明,实验已成功的将改进后的SPRINT算法移植到了基于云计算的平台HADOOP上,并对海量的数据集实现了准确率较高的分类挖掘。
5 结束语
在这个数据呈爆炸式发展的时代,各类企业对大规模及超大规模数据进行处理和和挖掘的强烈需求促生了数据挖掘以及云计算等技术。本文就是在这个大背景下,把数据挖掘分类算法同基于云计算的HADOOP集群框架进行结合,借助于其超凡的存储计算能力,达到了对海量数据挖掘的优化。
[1]蒋良孝,蔡之华.分布式数据挖掘研究[J].计算机与现代化,2002,85(9):4-7.
[2]戴元顺.云计算技术简述[J].信息通信技术,2010(2):29-35.
[3]Naohiro Ishii,TakahiroY amada,Yongguang Bao.Rough Set Based Learning for Classification[C].20th IEEE International Conference on Tools with Artificial Intelligence,2008(2):97-104.
[4]韩松来,张辉,周华平.基于关联度函数的决策树分类算法[J].计算机应用,2005,25(11):2655-2657.
- 长春理工大学学报(自然科学版)的其它文章
- 基于线阵CCD的小型光谱仪研究
- 大型圆柱件圆柱度误差测量方法研究
- 基于群组的WI-FI指纹室内定位研究

