Black-Litterman 模型在中国养老金入市投资中的应用

王海琳

（山东大学数学学院，山东 济南 250100）

一、研究背景

一方面，中国养老金目前的状况不容乐观。因此，养老金的增值保值问题成为热点问题。增值保值的一大方法是放弃养老金单一的投资方法，转而进行多渠道的投资，比如投资债券，股票等高收益的金融资产。2012年3月20日，中国广东省政府将千亿养老金交于全国社保基金理事会代理投资运营，这是对中国养老金投资运营的试点，也是中国在养老金管理和运营方面迈出的一大步。这表明中国养老金入市投资成为必然趋势。

养老金入市面临的首要问题是如何保证在高风险的市场中保证稳定的收益。想要解决这个问题，可以首先从对各种金融资产的投资比例进行研究，即如何分配投资的金融资产的各项比例来达到在风险一定的情况下获得最高的收益。

另一方面，针对如何确定最优投资比例的问题，Black-Litterman模型较好得解决了这个问题。Black-Litterman模型是由Fisher Black和Robert Litterman在1992年首先提出，是基于金融行业对马可威茨（Markowitz）均值-方差模型数十年的研究和应用的基础上优化。Black-Litterman模型利用概率统计方法，将投资者对大类资产的观点与市场均衡回报相结合，产生新的预期回报。Black-Litterman模型自提出来后，已逐渐被华尔街主流所接受，现已成为高盛公司资产管理部门在资产配置上的主要工具。

基于以上两点，本文将用Black-Litterman模型来解决如何最优化养老金在各项金融资产中的投资比例这一问题。

二、Black-Litterman模型

本文使用的对资产配置的模型为可融入主观观点的Black-Litterman（BL）资产配置模型。

（一）Black-Litterman 模型的简介

Black-Litterman模型对markowitz模型要用到的均值和方差的估计方法进行了改进，它采用贝叶斯分析框架来处理这两个预测值，使之能够融合组合管理人的主观观点。在这个方法下，组合管理人只需要提供任意数量的观点，模型就会把这些观点转化为明确的证券收益率预测和相关的协方差矩阵。因此，Black-Litterman模型解决了将观点翻译成明确的收益率的预测问题。而在Black-Litterman模型出现之前，没有办法可以直接地，系统地把观点或信息转化为明确的预测。

（二）Black-Litterman模型的推导

1.市场模型

假设市场中有N个资产，收益率服从

对于μ值，Black-Litterman采用了贝叶斯的看法。此模型把均值参数看作随机变量，即

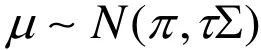
其中π是对μ的最佳估计。

市场均衡假设所有投资者为了最大化均值-方差的效用而进行无约束最优化

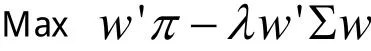
其中λ表示市场平均的风险规避系数，w：组合中资产所占权重向量。若weq表示均衡的市场组合的权重，由一阶条件可得相应的参照期望收益率

2.主观观点

BL模型中考虑关于预期收益率μ的观点，而且是线性的观点。设组合管理人对N 个资产产生了K 个观点，这K 个观点互不相关，用K×N的观点“选择”矩阵P 来表示。其中第k行表示第k个观点，这一行的每个元素表示对应期望收益率的相对权重，每个观点的权重和为1或0，分表表示绝对观点和相对观点。观点的期望收益向量用v来表示，协方差矩阵ΩK×K分别量化了观点及其不确定性，即组合管理人对观点的信心水平。由于观点互不相关，ΩK×K是对角矩阵。

举例说明，面对三种资产，组合管理人有两条观点：第一种资产的年收益率比第二种高3%，第三种资产的年收益率为5%。则其选择矩阵为

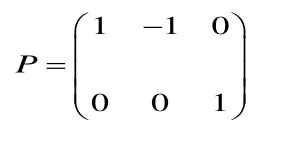
观点向量为v=（3%，5%）’。如果投资者对以上两个观点的信心水平为w1和w2，则其不确定性可用表示。

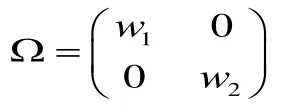
3.后验结果

利用贝叶斯公式从观点信息得到

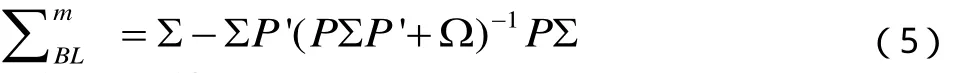
4.资产分配结果

在最优化的目标函数是Markowitz临界线算法，也就是市场均衡假设下所有投资者共享的效用函数，直接得到的优化结果是：

三、Black-Litterman模型对养老金投资比例优化的实证

文本首先针对运用black-litterman模型对养老金的投资方向的比例进行计算。

（一）假设

对养老金的投资方向做简化处理，下面只考虑国债，企业债券以及股票这三个投资渠道。

（二）数据分析及来源

本文采用的数据是国债指数，企债指数以及沪深300指数，时间区间是2011年4月1日至2013年3月31日，每种指数都有484个数据。之所以选择国债指数和企债指数是因为两者均是债券市场的晴雨表，他们的编制方法使得他们能够代表债券市场的收益情况；而选择沪深指数是因为此指数囊括上证和深证的有影响力和代表性的股票，因此也能较好的反应整体股市的情况和收益率。数据的来源是大智慧软件。

（三）以数据的均值与方差作为black-litterman模型的主观观点

选择均值和方差作为black-litterman模型的主观观点是因为长时间产生的多样本的均值与方差可以体现国债，公司债券以及股票相对稳定的收益率及风险情况，而这种情况可以作为组合管理人的主观观点。当然，由于组合管理人的观点具有很强的主观性，因此也可以有其他的方法来体现主观观点，如利用时间序列模型预测的结果作为主观观点等，但本文利用均值与方差作为对国债，企债和股票的主观观点。

我们采用以下的办法把指数变换成复利收益率：

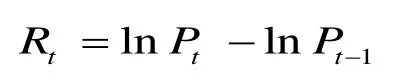
其中tP表示资产在t时刻的指数。

由于black-litterman模型中使用的是超额收益率，本文采用一年期的定期存款利率作为无风险收益率，年利率为3.25%，另外仍需把年利率转换为每天的利率来计算超额收益率。每天的利率是3.25%/365。下表是对国债，企债，股票收益率的描述统计数据。国债收益率的均值为0.0000622，标准差为0.000262；企债收益率的均值为0.000167，标准差为0.000564；股票的收益率的均值为0.000472，标准差为0.013182。

（四）把主观观点转换为可输入black-litterman模型的信息

其中P就是观点选择矩阵，由于本文对3种资产都发表了绝对观点，所以P 是3维的单位矩阵。

（五）应用Black-litterman模型获取后验分布

应用市场变量的black-litterman模型，结合组合管理人发表的观点及其不确定性，得到市场变量的后验分布。要想得到后验分布，我们还需要计算出市场均衡情况下的隐含收益向量π和各行业指数超额收益率的3维协方差矩阵Σ。

矩阵Σ易得，为

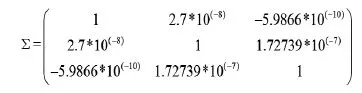
其中λ为风险规避系数。本文利用

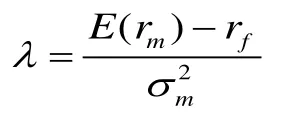
国债占0.2152%，企债占2.5535%，股票占97.2313%。

有了上述π，Σ，v，Ω，P的数据，就可以代入（2.4）（2.5），通过matlab的实现简单的矩阵代数运算可得到后验分布

（六）得出投资分配比例