一种半监督稀疏保持近邻判别嵌入算法

李世银，王 飞，彭 超

（中国矿业大学信息与电气工程学院，江苏徐州 221116）

一种半监督稀疏保持近邻判别嵌入算法

李世银，王 飞，彭 超

（中国矿业大学信息与电气工程学院，江苏徐州 221116）

保持近邻嵌入（NPE）算法对局部线性嵌入（LLE）算法进行了改进，克服了新来样本问题，但在处理分类问题上表现不足。基于此提出一种半监督稀疏保持近邻判别嵌入算法，该方法首先采用小波变换对数据进行预处理，然后执行等距离映射（Isomap）算法选择合适的低维嵌入维数，最后结合稀疏表示理论、NPE和线性判别分析（LDA）的思想，重构邻域图，并在建立目标函数时使得已标签信息中同类样本点之间相互靠近，异类样本点之间相互远离，未标签信息邻域信息得以保持。这样，既得到了高维映射函数，又提高了分类正确率。通过在人脸数据库上实验，并与其他半监督算法作比较，该算法在识别率上表现较好。

保持近邻嵌入;稀疏表示;线性判别分析;半监督

目前，在较为典型的降维方法中线性降维的方法主要有主成分分析（PCA）［1］、线性判别分析（LDA）［2］等，这些方法在处理具有线性结构的数据时表现出较好的优越性，但是在处理具有非线性数据结构时表现较差。后来出现的较为典型的流形降维方法，如等距离映射（Isomap）［3］、局部线性嵌入（LLE）［4］、Laplace 特征嵌入（Laplacian Eigenmaps）［5］等在处理非线性结构数据时表现较好，但是它们同时又都具有无法处理外来样本的缺点。为克服这些方法的缺点，文献［6］提出了保持近邻嵌入（NPE）算法，该方法能有效地处理外来样本的问题，但是该方法在处理分类问题时表现不足，因为它在线性重构时并没有对邻域的类别进行判断。文献［7］结合LDA思想，使得同类样本点分布尽可能密集，不同样本点分离，提出了一种新的半监督降维方法——半监督判别邻域嵌入（SSDNE），提高了识别率，但是该方法在选择邻域时依赖K值的选择，不能动态地反映数据之间的变化信息;文献［8］提出一种基于稀疏表示的半监督降维方法（SpSSDR），该方法结合稀疏表示和LDA思想，通过稀疏重构系数来同时定义图上边连接性及边权重，再结合边约束信息进行降维，但是容易忽略局部数据信息。综合上述文献的优点，本文结合稀疏表示思想、NPE和LDA算法，提出了一种基于半监督的保持近邻判别嵌入算法（SNPDE）。

小波变换是一种新的变换分析方法，它继承和发展了短时傅里叶变换局部化的思想，是进行信号时域分析的理想工具，在信号处理领域得到广泛的应用。在图像处理上，通过小波变换可将图像分解成不同尺度的低频分量和高频分量，低频分量保持图像的轮廓，高频分量保持图像的细节［9］。保留图像低频信息，适当去掉高频部分信息可以减少数据冗余，能很大程度地消除数据间的高频相关性，文献［10］把小波变换引入有监督增量式局部线性嵌入算法，提出了一种新的局部线性嵌入算法，用于人脸识别，提高了识别精度;而文献［11］把小波变换引入线性判别分析，提出了一种将人脸图像的小波分解和线性判别分析结合的人脸识别方法，提高了识别率。鉴于此思想，本文在数据预处理阶段引入小波变换思想，提取低频分量，然后再将处理后的数据应用到本文提出的算法中。

1 保持近邻嵌入算法

保持近邻嵌入算法（NPE）是局部线性嵌入（LLE）的线性逼近，能在降维后得到一个高维映射函数，弥补了LLE无法处理新来样本问题上的不足［6］。

设X={x1，x2，…，xn}∈Rm×n为训练样本，Y={y1，y2，…，yn}∈Rd×n为降维后训练样本的低维嵌入，n为样本数，m为样本维数，d为嵌入维数。NPE能在降维过程中得到一个投影矩阵W，将高维数据映射到一个低维d的特征空间中，即Y=WTX。NPE算法的具体步骤为:

首先，构造近邻图。与LLE类似，假定每个局部近邻是线性的，因此可以通过线性组合来描述局部的几何特征，选择每个样本点的K个近邻的构成近邻图。

然后，计算重建权值。近邻图中每一个训练样本xi用它的K近邻点xj线性重构，wij通过重建代价函数计算，公式为

式中:kn是xi的近邻个数。

最后，通过求解式（2）的广义特征向量得到线性映射关系

式中:M=（I-W）T（I-W），M是半正定矩阵。

2 基于半监督的保持近邻判别嵌入算法

2.1 数据预处理

2.1.1 小波变换

根据小波变换原理，低频部分具有较高的频率分辨力和较低的时间分辨力，在图像处理中，高频信号起到的作用非常微弱，而低频部分是针对有意义的某种尺度信号，对进一步的研究具有很好的帮助［9］。在运行本文提出的算法之前，首先对训练样本进行小波分解，并提取低频部分的数据作为人脸识别的特征矢量。图1是对ORL数据库中的一个图像的低频分量图，从左到右依次为:原始图像、进行小波1层分解和2层分解。原始图像大小为112×92，1层分解后图像大小为56×46，2层分解后图像大小为28×23。

2.1.2 Isomap 选择合适的维数

剩余方差描述的是低维特征空间中保持高维空间数据间几何关系的程度，剩余方差越小，表示这种几何关系保持的越好［3］。因此，本文在对高维数据降维前，并不是盲目选择某一低维进行降维，而是对高维数据先执行Isomap算法，通过剩余方差与维数之间的关系图来确定合适的低维嵌入维数。

图1 小波分解

2.2 稀疏重构权值

式中:X=［xi，x2，…，xn］为基信号矩阵;C 是重建系数向量;‖C‖0表示C的伪l0范数，用于衡量C的稀疏性，为C中非零元素的个数。针对上式条件存在的非凸问题，研究表明，只要所求的理论最优解足够稀释，则l0和l1问题等价，式（1）描述的优化问题的解唯一，且可以通过式（4）优化问题求解

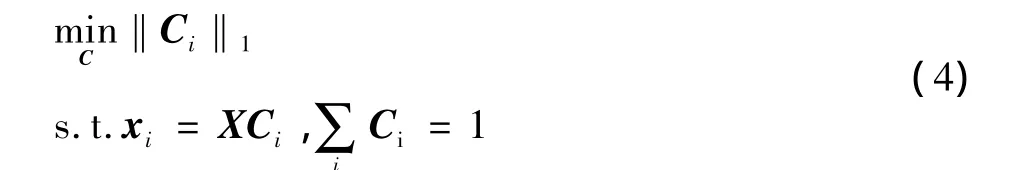
求解式（4）可以通过拉格朗日乘子法获得，即求解

同类样本离散度矩阵为

异类样本离散度矩阵为

未标签的样本，定义其上的稀疏保持项为

目标函数定义为

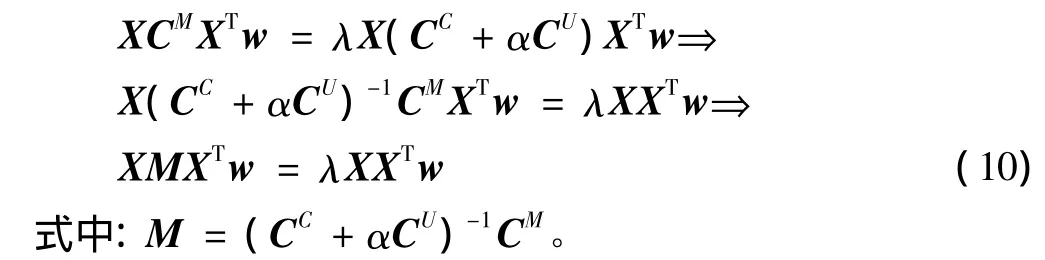
把上式的特征值从大到小排序λ0≥λ1≥…≥λd-1，对应的特征向量A={a0，a1，…，ad-1}，得到低维嵌入 yi=ATxi。

2.3 SNPDE 具体过程

综上所述，本文提出的具体算法步骤为:1）对训练样本进行小波分解，得到的数据运行Isomap选择合适的低维嵌入维数;2）根据标签信息和式（6）和式（7）分别计算同类样本离散度矩阵和异类样本离散度矩阵，根据式（8）计算未标签样本的稀疏保持项。

3 实验与分析

ORL标准人脸库是400个112×92灰度自然场景下的人脸图像，由40个测试者提供。其中人脸部分表情和细节均有变化，例如笑与不笑、眼睛睁着或闭着、戴或不戴眼镜等，人脸姿态也有变化，其深度旋转和平面旋转可达20°，人脸尺寸最多有10%的变化。在ORL人脸库上做实验，随机选择每个人5幅图像做训练样本，然后随机选择5幅作为测试样本，这样训练样本和测试样本总数均为200个。

另外，Jaffe人脸数据库，是在人脸表情识别研究中应用最多的数据库之一。包括216张人脸表情图像数据，每人20几幅分辨力为256×256的图像组成。在Jaffe人脸库上选10个人脸图像做实验，每个人均随机选择10幅图像做训练样本，另外随机选择10幅为测试样本，这样训练样本和测试样本总数均为100个。

首先，为验证小波分解的有效性，本文用ORL数据库分别对执行小波2层分解的NPE和未执行小波2层分解的NPE进行对比实验，结果如表1所示。

表1 未执行小波分解的NPE 算法与执行小波分解的NPE 算法比较

表1中的时间是NPE仅训练过程所用的时间，单位为s，可以看出执行小波分解和未执行小波分解的NPE算法中，最终的识别率相差不大，但时间上却节省了大约0.9 s，所以本文提出的算法在实验预处理上同样先进行小波分解。

本文实验对训练样本采用小波2层分解，对于ORL数据库分解后训练样本大小由原来的112×92降到28×23，Jaffe数据库分解后训练样本大小由原来的256×256降到64×64。然后分别对数据进行Isomap降维算法，得到剩余方差和维数关系图，如图2所示。对于ORL数据库，当维数大于10时，剩余方差变化就非常小了，因此这里可以选取低维空间大于10的维数，对于Jaffe数据库，选择大于20的维数，然后再分别运行PCA+LDA，NPE，NPDE，SpSSDR和SNPDE算法降到各维，最后采用1－NN分类器进行分类。

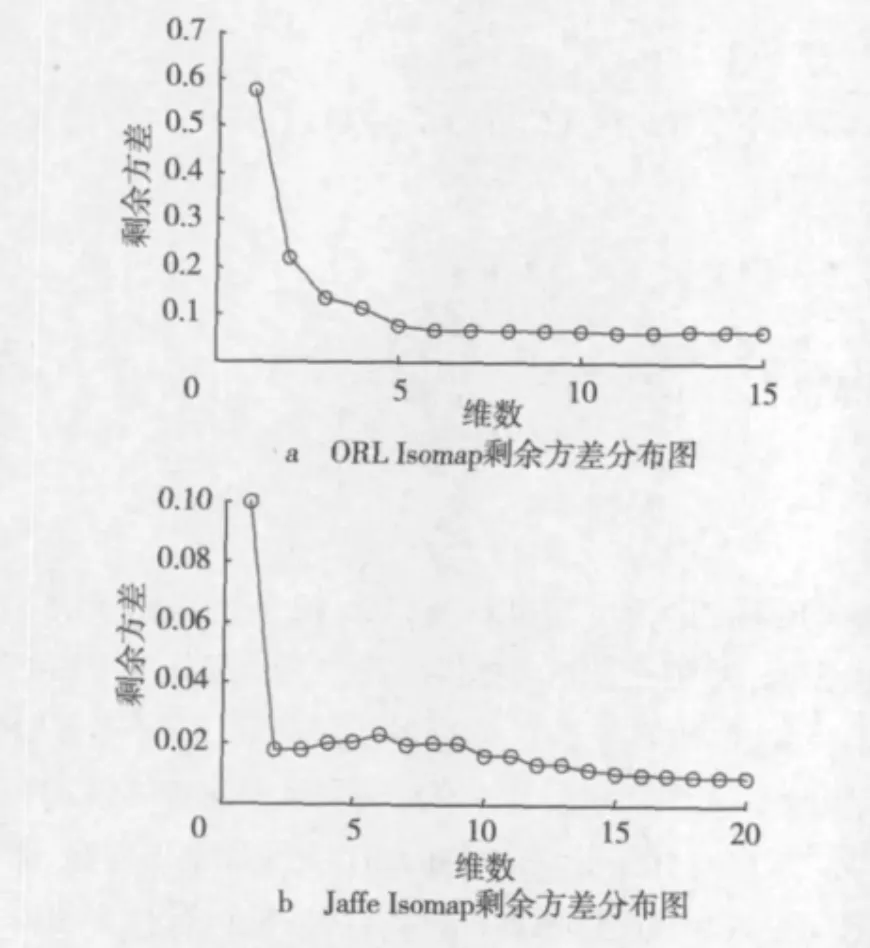
图2 剩余方差和维数关系图

实验中，近邻数K统一设置为10，α设置为0.01，为达到对比效果，本文分别对两个数据库进行不同维度下降维结果对比，为避免实验随机性，实验结果均为20次结果的平均值，实验结果如图3所示。图3a和图3b分别是ORL和Jaffe数据库中选择标签120和60个训练样本时各种算法的识别率，图3c和图3d分别是ORL和Jaffe数据库中选择标签80和40个训练样本时各种算法的识别率。

为了比较各种算法在不同目标维度下的性能，分别在ORL和Jaffe执行各算法，如图3a和图3b所示，本文提出的算法要优于其他算法，这是因为:人脸数据库是一种非线性结构，LDA方法在处理这些数据时，容易忽略局部数据信息，所以效果最差;SSDNE算法融合了NPE和LDA的思想，降维过程中，重构目标函数，既保证了局部数据信息，又使得同类样本点靠近，异类样本点远离，效果要好于NPE，但是在建邻近图时，K值的选择是人为的，容易丢失整体样本点之间隐藏的信息;SpSSDR引入了稀疏表示思想构建图，基于稀疏重构系数构建的图较其他算法构造的图具有更好的区分性，从而易于获得具有较好区分能力的判别子空间，其上的分类精度也较高，但是SpSSDR容易忽略数据间的局部信息;本文提出的算法SNPDE在重建图时，既引入了稀疏表示，又结合NPE思想保证了局部信息得以保留，最后的目标函数又结合了LDA思想，易于分类，所以效果最佳。另外，本文重做以上实验仅对三种半监督算法进行比较，但分别都减少了监督信息标签，如图3c和图3d所示，结果验证了本文算法的优越性，同时也可以看出，随监督信息标签减少，识别率也随之降低。

图3 实验结果

4 小结

本文提出了一种新的半监督降维方法，数据预处理部分选择小波分解，去掉了高频部分信息，很大程度地消除数据间的高频相关性，降低了维数，提高了算法的效率;通过执行Isomap算法选择了合适的低维嵌入维数进行降维，避免了低维选择的盲目性;新算法把稀疏表示理论引入到NPE算法中，重新构造了邻域图，保证了局部领域关系。同时，构建目标函数时又借助了LDA思想，既得到了映射函数，解决了新来样本问题，又提高了识别率。

:

［1］TURK M，PENTLAND A.Eigenfaces for recognition［J］.Journal of Cognitive Neuroscience，1991，3（1）:71－86.

［2］边肇祺，张学工.模式识别［M］.北京:清华大学出版社，2000.

［3］TENENBAUM J B，SILVA V D，LANGFORD J C.A global geometric framework for nonlinear dimensionality reduction［J］.Science，2000（290）:2319－2322.

［4］ROWEIS S T，SAUL L K.Nonlinear dimensionality reduction by locally linear embedding［J］.Science，2000（290）:2323－2326.

［5］BELKIN M，NIYOGI P.Laplacian eigenmaps for dimensionality reduction and data representation［J］.Neural Computation，2003（15）:1373－1396.

［6］HE X F，CAI D，YAN S C，et al.Neighborhood preserving embedding［C］//Proc.ICCV 2005.Washington D C:IEEE Computer Society Press，2005:1208－1213.

［7］刘志宇.一种半监督判别邻域嵌入算法［J］.计算机工程与应用，2011，47（19）:173－175.

［8］张春涛，郭皎，徐家良.基于稀疏表示的半监督降维方法［J］.计算机工程与应用，2011，47（20）:181－183.

［9］李春华，秦志英.图像的超小波稀疏表示［J］.电视技术，2012，36（13）:44－47.

［10］刘倩，潘晨.新的局部线性嵌入下的人脸识别方法［J］.计算机工程与应用，2011，47（24）:171－173.

［11］邓志国.基于小波变换和线性判别分析的人脸识别方法［J］.华东交通大学学报，2006（5）:102－104.

［12］MALLAT S G，ZHANG Z.Matching pursuits with time－frequency dictionaries［J］.IEEE Trans.Signal Orocessing，1993，41（12）:3397－3415.

Semi－supervised Sparse Neighborhood Preserving Discriminant Embedding Algorithm

LI Shiyin，WANG Fei，PENG Chao

（School of Information and Electrical Engineering，China University of Mining and Technology，Jiangsu Xuzhou 221116，China）

Neighborhood preserving embedding（NPE）algorithm is improved on Locally Linear Embedding（LLE）algorithm，and it overcomes the new coming sample problem，but it is not good in dealing with the classification.A semi－supervised sparse neighborhood preserving discriminant embedding algorithm is presented，the method preprocesses the data by using the wavelet transform，and then it performs Isomap algorithm to select the appropriate low－dimensional embedding dimension，and the last it reconstructs the neighborhood graph which is based on the theroy of sparse representations，NPE and linear discriminant analysis（LDA），at the same times，it makes closer between the same class points and away from each other between different class points which have been labeled，maintains the information of points which have been unlabeled.So the new algorithm has both got the high－dimensional mapping function，and it improves the classification accuracy.Experiments on face databases，comparing with other semi－supervised algorithms，the proposed algorithm performes better on the recognition rate.

NPE;sparse representation;LDA;semi－supervised

TP391

A

【本文献信息】李世银，王飞，彭超.一种半监督稀疏保持近邻判别嵌入算法［J］.电视技术，2013，37（3）.

徐州市科技计划项目（XX10A001）

责任编辑:时 雯

2012－07－15