基于格子Boltzmann方法的孔隙率对泡沫金属内相变材料融化传热的影响

张岩琛 杲东彦 陈振乾

(1东南大学能源与环境学院，南京 210096)

(2南京工程学院能源与动力工程学院，南京 211167)

基于格子Boltzmann方法的孔隙率对泡沫金属内相变材料融化传热的影响

张岩琛1杲东彦2陈振乾1

(1东南大学能源与环境学院，南京 210096)

(2南京工程学院能源与动力工程学院，南京 211167)

基于局部热非平衡条件在表征单元尺度上构建出双温度分布函数的格子Boltzmann方程，用该方程来表征泡沫金属骨架与相变材料融化传热的温度场，用密度分布函数演化方程来表征融化液相速度场.然后模拟了泡沫金属内相变材料融化界面位置随时间的变化及金属骨架和相变材料的温度分布情况.模拟结果与其他文献的计算结果吻合较好.重点分析了泡沫金属孔隙率对相变材料融化传热的影响.结果表明，孔隙率的减少有利于增强金属骨架热传导换热的作用，但也会导致自然对流传热的降低及相变材料蓄热量的减少.因此在设计泡沫金属蓄热装置时，对于孔隙率的确定需要结合工程需求进行选择.

格子Boltzmann方法;泡沫金属;相变材料;固液相变

泡沫金属是一种具有一定刚度和强度、孔隙率高、密度低及传热效率高的新型功能材料［1］.固/液相变储能材料由于相变潜热大、相变前后体积变化小被广泛应用于相变储能、航天器件热防护及电子器件温度控制系统等.然而目前很多常规的相变材料导热系数都比较小，导致了整体的传热速率及冻融速度相对较低.综合考虑泡沫金属和相变材料的功能特点，可以采用泡沫金属作为骨架和强化传热的材料，内部填充相变蓄热材料，从而开发出具有较高传热速率的蓄热装置.

目前关于泡沫金属填充相变材料的融化传热过程的研究相对较少.大多数研究是关于低孔隙率、低渗透率的填充床类多孔介质内融化、凝固相变传热过程，且能量方程大多数采用的是基于局部热平衡条件假设的单温度方程［2］.与传统的多孔介质相比，泡沫金属具有高孔隙率、高渗透性、强局部热非平衡效应等特性.Krishnan等［3］基于双温度模型采用有限体积法数值模拟了泡沫金属内相变材料融化相变过程.彭冬华等［4］采用有限体积法数值模拟了泡沫金属内填充石蜡的融化传热过程.而实验研究［5］表明，孔隙率、孔密度对融化传热过程有着一定的影响.王杰利等［6］的实验研究表明泡沫金属孔隙率对融化传热影响较大，而孔密度对融化传热的影响相对比较小.受实验研究［5－6］启发，本文在数值研究［2－3］基础上，尝试构建包含孔隙率等几何结构因素的泡沫金属内相变材料融化传热过程的数学模型，并通过数值模拟手段来分析孔隙率等几何结构因素对融化传热过程的影响.

格子Boltzmann方法(简称LBM)是近20多年来发展起来的一种不同于传统数值计算方法的流体计算和建模新方法.该方法在许多传统计算方法难以胜任的领域，如多孔介质、多相流等，都取得了成功的应用.近年来已经将格子Boltzmann方法用于研究固液相变传热问题，然而大多数研究均针对无多孔介质的固液相变问题［7－9］;另一方面，Guo等［10］在表征单元(REV)尺度上构建了描述多孔介质内自然对流的双分布函数的格子Boltzmann模型，表明格子Boltzmann方法模拟多孔介质流动及传热的可行性.Seta等［11］进一步验证了格子Boltzmann方法模拟多孔介质内自然对流的正确性.然而这些模型［10－11］中都没有涉及具有相变的自然对流过程，且能量方程采用的是单温度方程.因此已有的格子Boltzmann模型并不能直接应用在泡沫金属系统内融化传热过程中.

本文将基于局部热非平衡条件构建出表征泡沫金属内融化相变的格子Boltzmann模型并进行数值模拟，重点分析孔隙率对融化传热过程的影响.

1 控制方程

控制方程假设条件:① 在多孔介质骨架与孔隙内相变物质之间处于局部热非平衡;② 在表征单元尺度上有自然对流.

1)连续性方程

2)动量方程

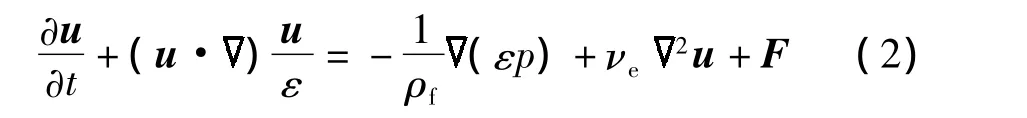
3)泡沫金属骨架的温度方程

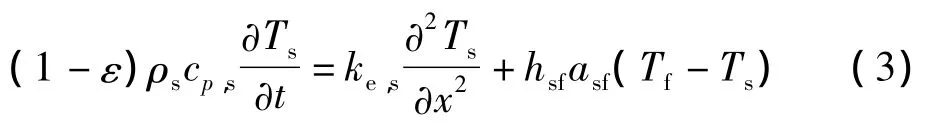
4)相变材料的温度方程

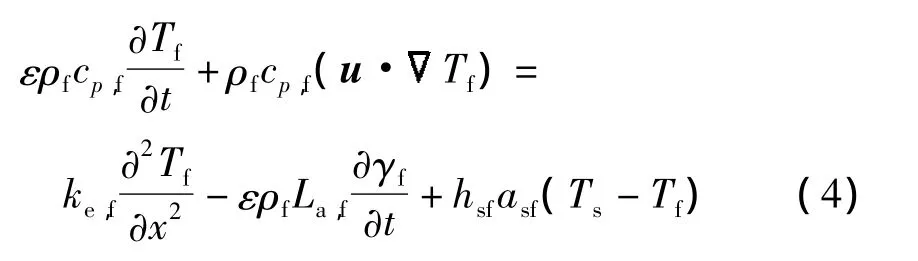
方程(1)～(4)中，下标f，s分别表示相变材料及泡沫金属骨架;ε 为孔隙率;u，p，F，T，ρ，νe，ke，cp，La，γf分别为宏观渗流速度、压力、体积力项、温度、密度、有效黏性系数、有效导热系数、定压比热、融化潜热和融化液相比;hsf，asf分别为内部热交换系数和内部热交换面积.其中体积力项为

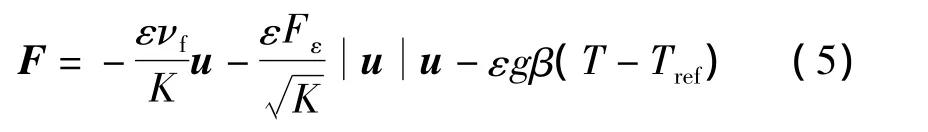
式中，K和Fε分别为多孔介质渗透率和形状因子;νf和β分别为流体动力黏性系数及热膨胀系数;Tref为参考温度.方程(5)中右边第1项和第2项分别为线性(Darcy)和非线性(Forchheimer)介质阻力，右边第3项为浮升力.此外方程(2)中右边第2项是体现边界作用的Brinkman黏性项，因此式(2)又称Brinkmann-Forchheimer-Darcy方程.

为了求解方程组(1)～(4)，必须给出相关参数或方程，其中固体骨架与相变材料有效导热系数的经验模型为［12］

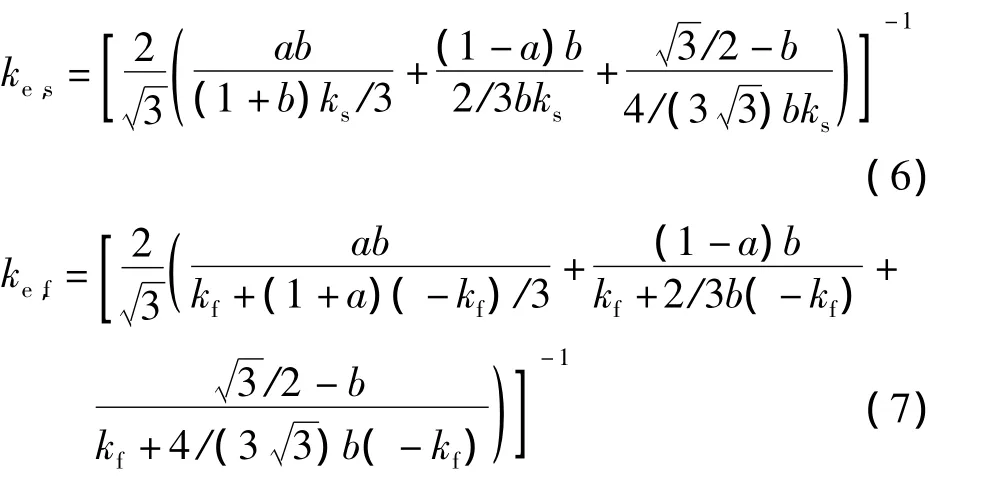
式中，参数a=0.09;参数b可根据孔隙率ε和参数a的表达式求出，即

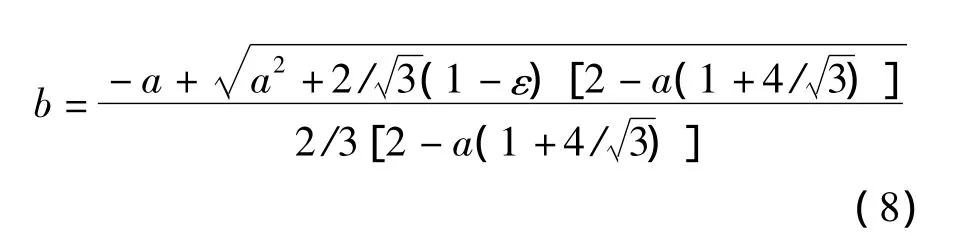
泡沫金属内部有效热交换面积asf为［13］

式中，df和dp分别为孔纤维直径、平均孔径，两者与孔隙率ε相关关系为［14］为

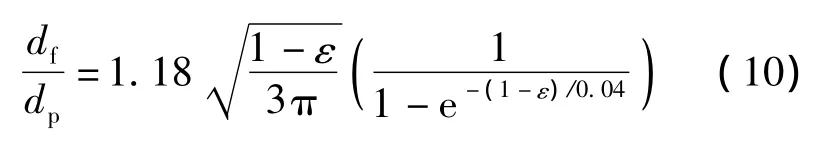
内部热交换系数hsf［14］为

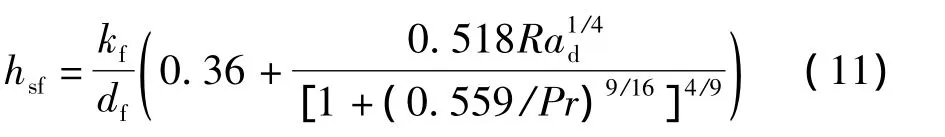
式中，局部Rayleigh数.此外渗透率K和形状因子Fε参数为［12］

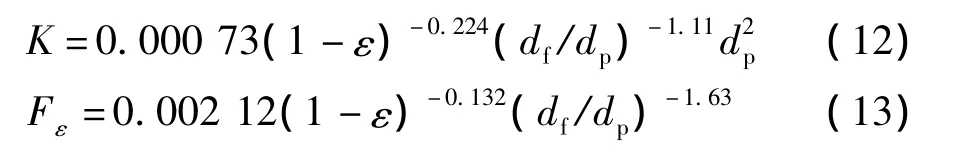
2 格子Boltzmann模型

在模拟泡沫金属内相变材料融化传热过程中，速度场密度分布函数fi的LBM方程为

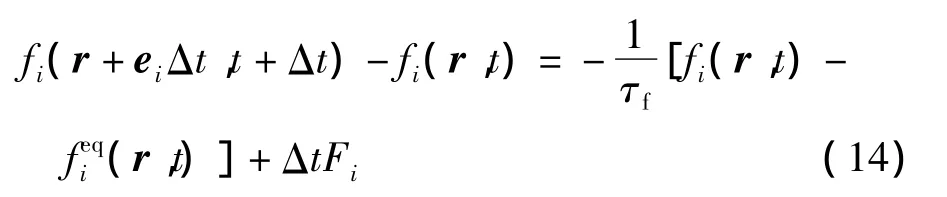
式中，r为空间矢量位置;t为时间;i表示格子离散速度的方向;ei为格子离散速度;Δt为时间步长;τf为无量纲松弛时间;fieq为平衡态密度分布函数;Fi为离散作用力项.方程(14)相关参数设置及表达式的详细信息可见文献［10］.由于融化传热方程式(3)、(4)中含有源项，不能直接采用Guo

等［10］基于局部热平衡条件下针对多孔介质内自然对流传热提出的温度分布函数演化方程，因此，需要构建表征融化温度场的分布函数演化方程.Shi

等［15］提出了非线性对流扩散方程的LBM模型，该模型通过选择适当的平衡态分布函数及非线性源项，使模型能够准确地回归到相应的宏观方程.因此本文采用非线性对流扩散方程格子Boltzmann

模型构建泡沫金属骨架及相变材料温度分布函数格子Boltzmann方程:

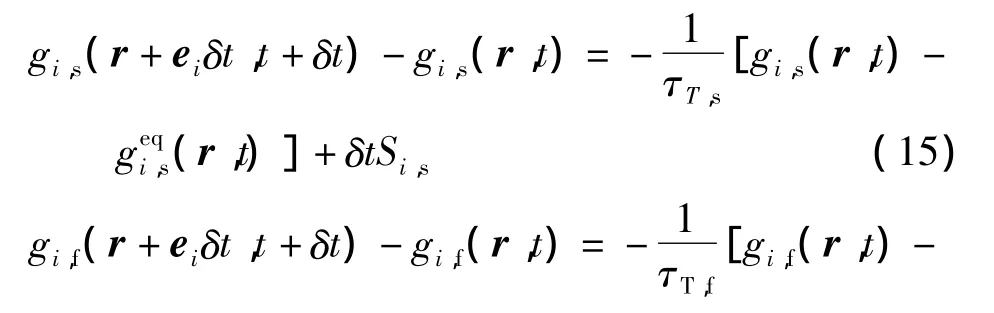
式中，τT为温度分布函数无量纲松弛时间参数;geqi为平衡态分布函数;Si为演化方程离散源项.平衡态分布函数geqi及源项Si表达式为

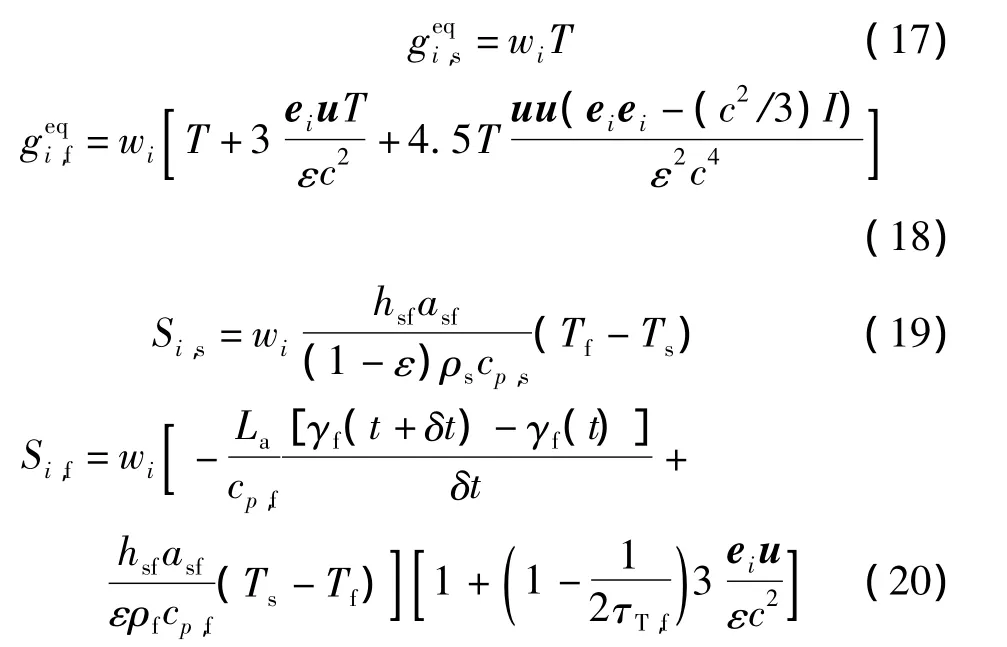
式中，wi为格子方向相关的权系数;格子速度c=Δx/Δt，Δx为格子步长.无量纲松弛时间参数 τT，s，τT，f定义为

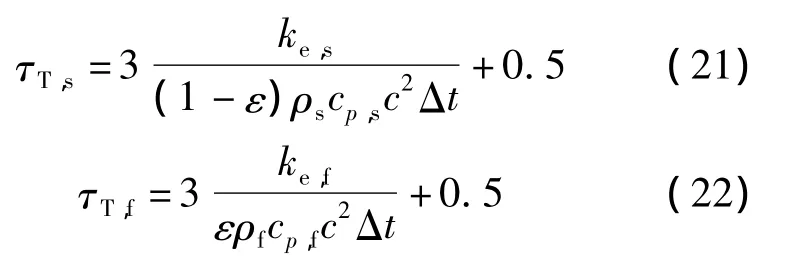
温度定义为T=∑gi.通过Chapman-Enskog多尺度展开，式(16)、(17)可回归到相应的宏观方程(3)和(4).

采用格子Boltzmann方法进行模拟时，不同的边界条件会直接影响到模拟的精度和稳定性.本文在速度边界条件处理上，采用Guo等［16］提出的具有二阶精度的非平衡外推格式，热边界条件处理采用Tang等［17］提出的非平衡外推格式.

3 计算结果及讨论

3.1 模型验证

由于目前尚没有可用来检验模型的实验研究资料，所以利用模拟结果与文献［3］中控制体积法计算结果进行对比，以验证模型的正确性.文献［3］的计算对象为一个二维矩形区域，高为H，宽为L=H，区域内是孔隙率为ε=0.8的泡沫金属，泡沫金属孔隙内填充固体相变材料.计算区域左壁为恒热温壁面，其无量纲温度设置为Th=1.0，右壁为恒冷温壁面，其温度为Tc=0.0，上、下壁面为绝热壁面，区域初始温度Ti=0.0，相变材料的融化温度为Tm=0.3.其他重要的无量纲参数设为:dp/H=0.013 5，Ra=gβ(Th－Tc)H3/(νfαf)=1.0×108，Da=K/H2=1.0 × 10－4，St=cp，f(Th－Tc)/La=1.0，Pr= νf/αf=50.0，局部Nui，d=hsfasfdp2/kf=5.90，热传导系数比 λ =ks/kf=1 000，Ω = ρscp，s/(ρfcp，f)=1.0，Fε=0.068，黏性比J= νe/νf=1.0.图1给出了LBM模拟结果与文献［3］数值计算结果的对比，图中无量纲时间 θ=(Fo)(St)=tαf/(H2St).由图可见，LBM模拟结果与文献［3］数值计算结果吻合较好，因此在一定程度上验证了LBM模型的正确性.图1(a)是孔隙率为0.8的泡沫金属材料中相变材料融化界面随时间的变化.由图可见，在自然对流的作用下，融化截面不断增大而越来越弯曲.图1(b)是孔隙率为0.8的泡沫金属骨架与相变材料温度的变化.金属骨架由于导热系数较高，在左侧加热作用下温度上升较快，而蓄热材料温度上升会慢一些.此外，蓄热材料在相变温度为0.3时发生相变，在局部地区温度维持相变温度不变，而金属则继续升温，所以当相变材料温度在0.3时，与骨架的温度相差最大.这一区域表现出局部热非平衡效应的特征，相变材料融化区差异最明显，而最终差异随时间的增大而变小.

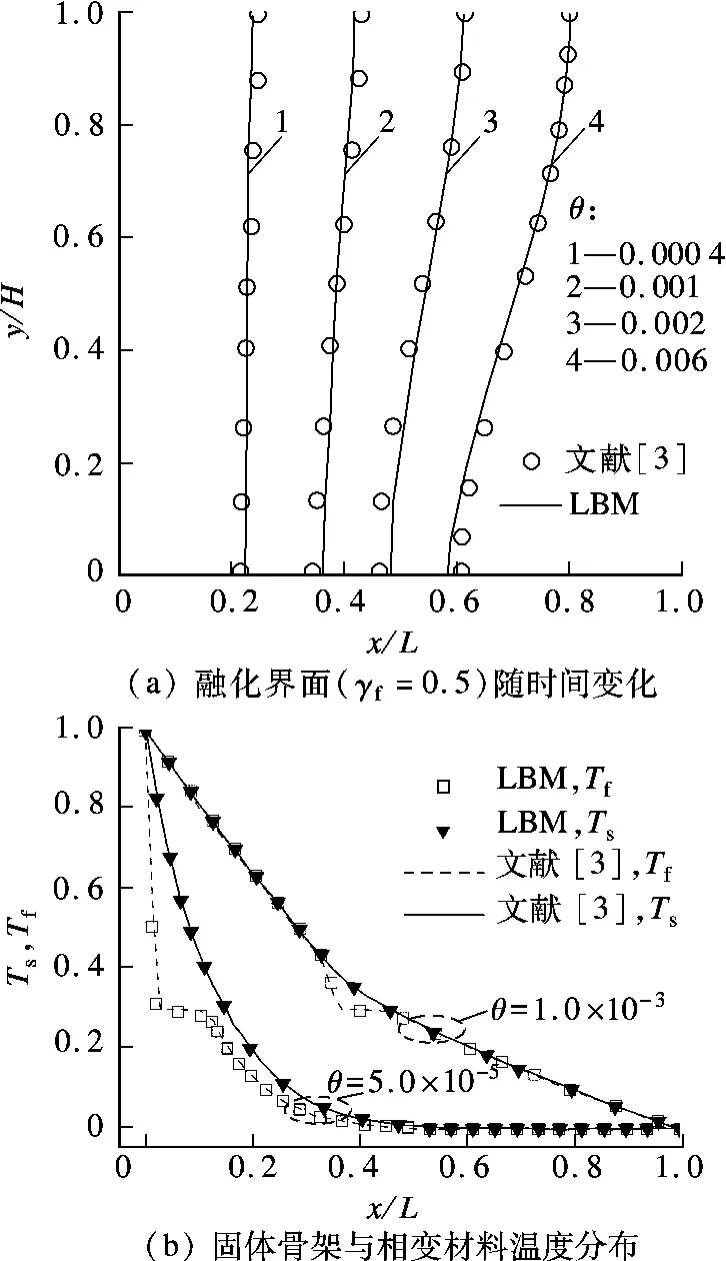
图1 LBM模拟结果与文献［3］数值结果对比

3.2 泡沫金属孔隙率对相变材料融化传热的影响

用LBM模拟了在不同孔隙率情况下相变材料的融化传热过程.物理模型同图1相同，主要相关参数为:L/H=1.0，dp/H=0.1，Th=1.0，Tc=0，Ti=0，Tm=0.3，Ra=1.0 ×108，Pr=50，St=1.0，J=1，λ =1 000，Ω =1.0.采用融化液相比V*和热壁面平均Nu来定量比较泡沫孔隙率对融化传热的影响，其定义分别如下:

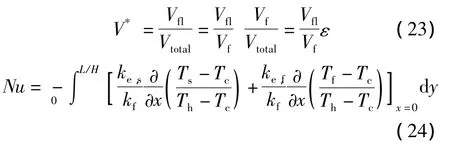
式中，Vfl，Vf，Vtotal分别为相变材料融化液相体积、相变材料总体积和区域总体积.图2为泡沫孔隙率对融化传热的影响.从图中可以看出，在目前孔隙率范围内随着孔隙率的降低融化率在增加，这说明孔隙率降低虽然会导致一定程度上削弱自然对流作用，但较大提高了金属骨架的热传导作用，且后者处于主导作用;但当孔隙率进一步降低时，融化率的增大幅度越来越小，这说明孔隙率小到一定程度后，可能会导致自然对流效应大幅度的降低而影响整体传热.由图2(b)可见，随着孔隙率的降低平均Nu随着增加，这主要是孔隙率越小，其金属骨架传热越大，初始Nu就大，但孔隙率越小其下降的幅度越大，因此孔隙率小的系统其自然对流传热就弱.LBM模拟的结果与文献［5－6］的实验研究结论一致.

图2 泡沫金属孔隙率对融化传热的影响

此外，孔隙率的减少意味着装置中泡沫金属材料比例增大，相变材料的比例相应减小，从而导致整体蓄热量的减少.因此在设计蓄热装置时，需要考虑对蓄能量和相变传热速度的实际需求和约束条件，并对泡沫金属材料孔隙率进行优化选择.

4 结论

1)格子Boltzmann方法模拟的结果与文献［3］数值计算结果一致，方法的可行性和模型的适用性得到了一定验证.

2)孔隙率的减小有利于增强金属骨架热传导换热的作用，但也会导致自然对流传热的降低.在一定孔隙率范围内，骨架的热传导换热起主导作用，对流换热起次要作用，孔隙率的减少将导致融化率的增大，但增加幅度会减小.此外，孔隙率的减少也会导致储能容量减小.因此，孔隙率的选择需要综合考虑和优化选择.

3)对于表征单元尺度上的流动及传热模型，其精度受到参数模型的限制，因此能够计算预测几何结构相关参数的孔隙尺度微观模型仍需进一步研究.

［1］Hutter C，Buchi D，Zuber V，et al.Heat transfer in metal foams and designed porous media［J］.Chemical Engineering Science，2011，66(17):3806－3814.

［2］Gao D Y，Chen Z Q.Lattice Boltzmann simulation of natural convection dominated melting in a rectangular cavity filled with porous media［J］.International Journal of Thermal Sciences，2011，50(4):493－501.

［3］Krishnan S，Murthy J Y，Garimella S V.A two-temperature model for solid-liquid phase change in metal foams［J］.Journal of Heat Transfer，2005，127(9):995－1004.

［4］彭冬华，陈振乾，施明恒.泡沫金属内相变材料融化传热过程的数值模拟［J］.工程热物理学报，2009，30(6):1025－1028.

Peng Donghua，Chen Zhenqian，Shi Minheng.Numerical simulation of phase change material thawing process in metallic foams［J］.Journal of Engineering Thermophysics，2009，30(6):1025－1028.(in Chinese)

［5］Lafdi K，Mesalhy O，Shikh S.Experimental study on the influence of foam porosity and pore size on the melting of phase change materials［J］.Journal of Applied Physics，2007，102(8):083549.

［6］王杰利，屈治国，李文强，等.封装有相变材料的金属泡沫复合散热器实验研究［J］.工程热物理学报，2011，32(2):295－298.

Wang Jieli，Qu Zhiguo，Li Wenqiang，et al.Experimental study of hybrid heat sink sintered with metal foams filled with phase change materials［J］.Journal of Engineering Thermophysics，20011，32(2):295－298.(in Chinese)

［7］Semma E A，Gauaoui M E，Bennacer R.Lattice Boltzmann method for melting/solidification problems［J］.Comptes Rendus Mecanique，2007，335(5/6):295－303.

［8］杲东彦，陈振乾.格子Boltzmann方法模拟自然对流条件下融化传热过程［J］.计算物理，2011，28(3):390－396.

Gao Dongyan，Chen Zhenqian.Lattice Boltzmann method for heat transfer in melting with natural convection［J］.Chinese Journal of Computational Physics，2011，28(3):390－396.(in Chinese)

［9］Huber C，Parmigiani A，Chopard B，et al.Lattice Boltzmann model for melting with natural convection［J］.International Journal of Heat and Fluid Flow，2008，29(5):1469－1480.

［10］Guo Z L，Zhao T S.A lattice Boltzmann model for convection heat transfer in porous media［J］.Numerical Heat Transfer Part B，2005，47(2):157－177.

［11］Seta T，Takegoshi E，Okui K.Lattice Boltzmann simulation of natural convection in porous media［J］.Mathematics and Computers in Simulation，2006，72(2/3/4/5/6):195－200.

［12］Calmidi V V.Transport phenomena in high porosity metal foams［D］.Boulder，USA:University of Colorado，1998.

［13］Calmidi V V，Mahajan R L.Forced convection in high porosity metal foams［J］.Journal of Heat Transfer，2000，122(3):557－565.

［14］Churchill S W，Chu H H S.Correlating equations for laminar and turbulent free convection from a vertical plate［J］.International Journal of Heat and Mass Transfer，1975，18(11):1323－1329.

［15］Shi B C，Guo Z L.Lattice Boltzmann model for nonlinear convection-diffusion equations［J］.Physical Review E，2009，79(1):016701.

［16］Guo Z L，Zheng C G，Shi B C.An extrapolation method for boundary conditions in lattice Boltzmann method［J］.Physics of Fluids，2002，14(6):2007－2010.

［17］Tang G H，Tao W Q，He Y L.Thermal boundary conditions for the thermal lattice Boltzmann equation［J］.Physical Review E，2005，72(1):016703.

Influence of porosity on melting of phase change materials in metal foams with lattice Boltzmann method

Zhang Yanchen1Gao Dongyan2Chen Zhenqian1

(1School of Energy and Environment，Southeast University，Nanjing 210096，China)
(2School of Energy and Power Engineering，Nanjing Institute of Technology，Nanjing 211167，China)

Under local thermal non-equilibrium conditions，a lattice Boltzmann model based on double temperature equations was constructed to characterize the temperature field of metal foams framework and heat conduction of phase change materials in metal foams，and a equation based on density distribution function was constructed to characterize the velocity field of melt fluid.The melting front locations as a function of time and the temperature field were simulated by the lattice Boltzmann model.The results agree well with the results obtained in other literature.Then，the effects of porosity on the melting processes of phase change materials were investigated.The results show that the decrease of the porosity results in the increasing conduction heat transfer，the decreasing convection heat transfer and the decreasing heat storage capacity.Therefore，it is suggested to consider engineering requirements to determine porosity in the design of the foam metal heat storage device.

lattice Boltzmann method;metal foams;phase change materials;solid-liquid phase change

TK124

A

1001－0505(2013)01-0094-05

10.3969/j.issn.1001－0505.2013.01.018

2012-09-27.

张岩琛(1986—)，男，硕士生;陈振乾(联系人)，男，博士，教授，博士生导师，zqchen@seu.edu.cn.

国家自然科学基金资助项目(50776015，51206076)、“十二五”国家科技支撑计划资助项目(2012BBA07B02)、科技部国际科技合作技术交流专项资助项目(2011DFA60290).

张岩琛，杲东彦，陈振乾.格子Boltzmann方法研究孔隙率对泡沫金属内相变材料融化传热的影响［J］.东南大学学报:自然科学版，2013，43(1):94－98.［doi:10.3969/j.issn.1001－0505.2013.01.018］