基于随机计算的LDPC译码初始化实现方法﹡

尚生珑， 秦晓卫， 戴旭初

（中国科学技术大学 电子工程与信息科学系，安徽 合肥 230027）

0 引言

LDPC码，最早由 Robert G. Gallager博士于1963年提出，它具有逼近Shannon限的良好性能，目前已广泛应用于深空通信、光纤通信、卫星数字视频等领域。文献[1]中首次提出了运用逻辑门电路来实现二进制 LDPC（以下都为二进制 LDPC）译码的思想，而真正运用随机计算（Stochastic Computation）实现 LDPC译码是在文献[2]中提出。文献[3-6]针对迭代译码公式的实现分别提出了Supernodes、TFM、Delayed以及EM等方法。针对译码延迟的问题，文献[7]中提出了 NDS（Noise Dependent Scaling）的方法，对初始化公式进行放缩，以增加随机比特之间的信息交换。

然而在利用随机计算进行 LDPC译码的过程中，初始化公式的计算大多采用存储器的方法来实现。但采用存储器的方法会大大增加电路的面积。文献[5]中根据初始化公式的对称性，提出存储一半数据，而另一半数据通过比特翻转得到的方法，降低了硬件复杂度。为了进一步降低其实现复杂度，利用随机计算的方法来实现初始化公式的计算。

1 基于随机计算的初始化硬件实现方法

1.1 初始化公式的线性近似

在高斯白噪声信道下，采用 NDS方法，对似然比进行放缩，得到LDPC译码初始化公式为：

对接收到的符号值做进一步的限定，当接收到的符号值大于4或小于-4时都判决为4或-4，对符号值进行映射，转换到概率域上，有iy′=，于是公式（1）转换为：为降低实现复杂度，避免使用存储器，首先对公式进行线性近似，线性近似分段的准则是：

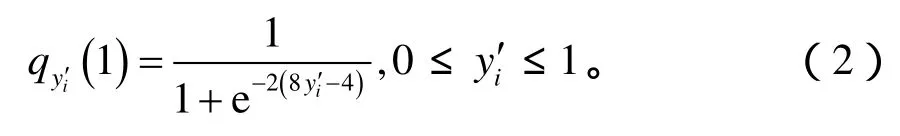
准则 1：分段数越少则线性公式越简单，实现复杂度越低，但近似误差越大，译码误差越高；反之，分段数越多则近似误差越小，译码误差越低，但实现复杂度越高。

准则 2：当似然值接近 0或接近 1时，较大的近似误差对译码的性能影响很小，因而近似误差可以较大；当似然值接近 0.5时，较大的近似误差对译码的性能影响较大，因而近似误差应该尽量较小。

考虑准则1采用3段线性近似，考虑准则2线性近似函数在 0.5处应该尽可能接近原函数，对公式（2）求二阶导数并令其等于0有：

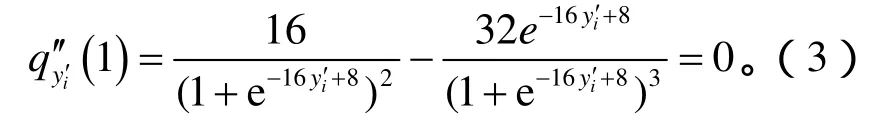
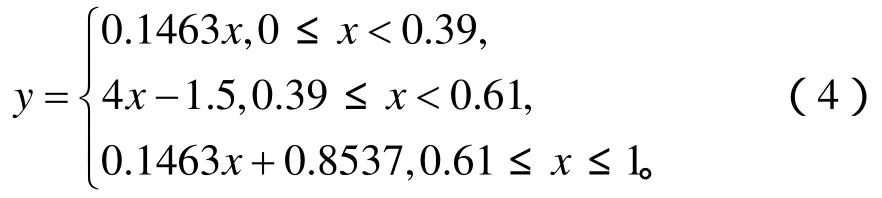
1.2 译码公式的随机计算实现

图 1给出了利用随机计算实现公式（4）的硬件框图，其中区间选择器得到数据所在区间，数据变换完成公式的计算，随机比特流产生器将数据转换为随机比特序列，运算电路实现公式在概率域上的计算，其中0.1463x通过简单的与门来完成，则可变换为通过一个非门以及一个与非门来完成计算。

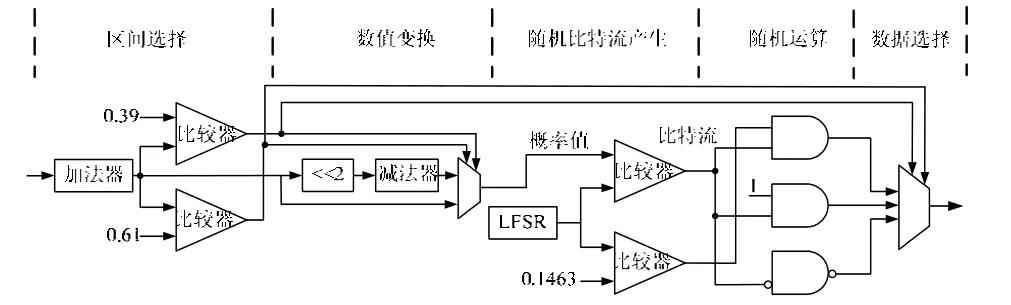
图1 基于随机计算的初始化硬件实现框

2 译码性能及实现复杂度

2.1 译码性能

为了比较该方法的性能，采用不同长度的LDPC码在不同性噪比下，同存储器方法以及和积算法方法进行了比较。图 2给出了（16,8）LDPC码的译码性能[8-9]，可以看出利用文中方法同存储器方法的译码性能基本相同。

图2 （16,8）LDPC码译码性能比较

图3给出了采用IEEE 802.16e[11]标准中的非规则（1056,528）LDPC码的译码性能比较，可以看出在低信噪比环境下，文中方法与存储器方法在译码性能上基本相同，在高信噪比环境下，译码性能约有0.15 dB的损失。

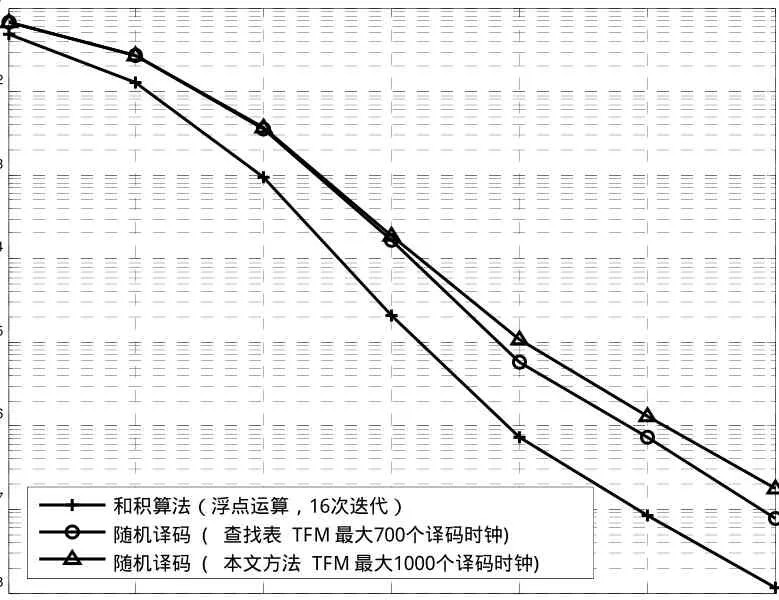
和积算法（浮点运算，16次迭代）随机译码 ( 查找表 TFM 最大70 0个译码时钟)随机译码 ( 本文方法 TFM 最大1000个译码时钟)

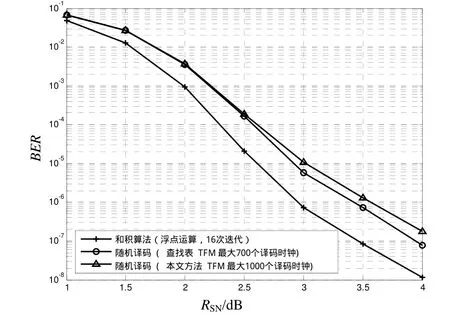
图3 （1056,528）LDPC码译码性能比较

2.2 实现复杂度

表 1给出了运用存储器方法、文献[10]的方法以及文中方法实现初始化公式的硅片面积。可以看出采用文中方法相比于存储器方法以及文献[10]的方法在面积上分别减少了54%和37%。

表1 实现初始化公式的电路面积比较

表 2给出了运用不同的方法实现（16,8）全并行LDPC随机译码所得到的硅片面积，当迭代公式采用文献[4]中提出的 TFM 方法时，运用文中的方法在面积上分别减少了8.6%以及13.2%，而当迭代公式采用文献[5]中提出的 DS方法时，运用文中的方法在面积上分别减少了12.3%以及23.5%。

表2 实现（16,8）LDPC译码器的电路面积比较

最后，利用文中方法和文献[10]的方法，在Xilinx-Virtex-4 XC4VLX200下实现（1056,528）LDPC译码器，表 3给出了利用文中的方法以及文献[10]中的方法所占用的 FPGA资源情况，可以看出利用文中的方法所需要的 4输入查找表个数比文献[10]的方法减少了12.8%。

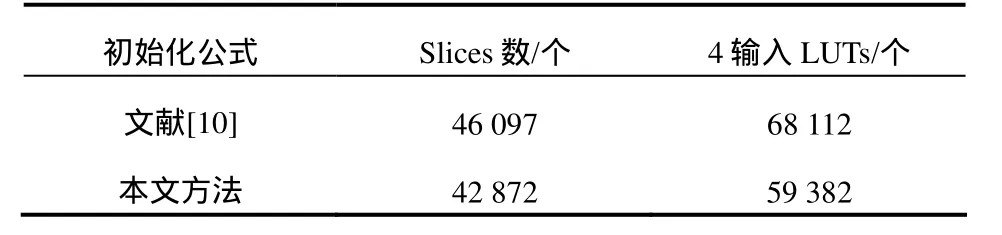
表3 （1056,528）LDPC译码器在FPGA上所占资源比较

3 结语

文中提出了一种基于随机计算的LDPC译码初始化公式的硬件实现方法，避免了使用存储器，实验证明，该方法适合于短LDPC码，或低信噪比情况下的长LDPC码。该方法相比于存储器方法在硅片面积上减少了37%，并使译码器的总体面积减小了12.3%，当采用FPGA实现时，该方法使得相应的4输入查找表个数减少了12.8%。

[1] KSCHISCHANG F R.Factor Graphs and the Sumproduct Algorithm[J]. IEEE Transactions on Information Theory,2001(47):498-519.

[2] GAUDET V C,RAPLEY A C.Iterative Decoding Using Stochastic Computation[C].USA:[s.n.],2003:299-301.

[3] WINSTEAD C.Stochastic Iterative Decoders[D].USA:Utah State University,2005.

[4] TEHRANI S S.Tracking Forecast Memories in Stochastic Decoders[C]. USA: IEEE International Conference on, 2009:561-564.

[5] NADERI A.Delayed Stochastic Decoding of LDPC Codes,Signal Processing[C].USA:IEEE Transactions on,2011:5617-5626.

[6] 任祥维,文红,张颂.LDPC码的全并行概率译码[J]. 通信技术,2011,44(08):42-44.

[7] TEHRANI S S.Survey of Stochastic Computation on Factor Graphs[C].USA:IEEE,2007:54-54.

[8] 黄琪,李丹,汪洋.一种优化 LDPC码环分布的改进算法[J].通信技术,2010,43(05):56-57,60.

[9] 张志亮,卿粼波,刘英.一种线性编码半随机构造 LDPC码及其仿真[J].通信技术,2009,42(02):12-14.

[10] TEHRANI S S. Fully Parallel Stochastic LDPC Decoders[C].USA:IEEE,2008:5692-5703.

[11] 邵湖,赵恒凯.LDPC码在 IEEE802.16e标准中的编译码分析[J].信息安全与通信保密,2011(07):45-47.