无谐振峰减振器在雷达晶体振荡器上的应用*
冯永平,帅立国,钟剑锋,刘国维
(1. 东南大学机械学院, 江苏 南京 211189; 2. 南京电子技术研究所, 江苏 南京 210039)
无谐振峰减振器在雷达晶体振荡器上的应用*
冯永平1,帅立国1,钟剑锋2,刘国维2
(1. 东南大学机械学院, 江苏 南京 211189; 2. 南京电子技术研究所, 江苏 南京 210039)
分析了振动环境对某雷达晶体振荡器的影响,并以此为依据设计了一种轻质的无谐振峰钢丝绳减振器,并与橡胶减振器进行了对比。实验结果表明,在基本保证减振效果的前提下,钢丝绳减振器更适合低温环境使用,晶体振荡器相位噪声相对橡胶减振器高出9~18 dBc/Hz @100Hz,可以在宽温度范围内用于地面、机载、舰载、球载等条件下的晶振减振。
晶体振荡器;钢丝绳减振器;轻质;相位噪声;低温
引 言
随着现代雷达技术的发展,电子元器件的稳定度要求越来越高。作为电子元器件中不可缺少的核心部件,晶体振荡器的稳定性将直接影响到整个雷达系统的作战性能。而晶体振荡器在振动环境下极易受到影响[1],会产生频率漂移和相位噪声,严重时会产生灾难性的后果。因此有必要对晶体振荡器采取隔振措施,以保证系统工作的精确度和稳定度。
无谐振峰减振器作为一种已在电子产品上广泛应用的减振结构,具有温度适应范围宽、无谐振峰的优点。其在晶体振荡器减振上的应用多使用压簧结构,这样不仅占用很大的空间,而且增加模块的重量,在雷达中的应用受到了很大的挑战。
本文从宽温度范围出发,基于无谐振峰减振器工作原理,设计了一种针对晶体振荡器的无谐振峰钢丝绳减振器,其结构更轻质、空间更小巧、走线更方便、维护更简易,并进行了与橡胶减振器的减振效果实验对比研究。
1 无谐振峰减振系统的理论分析
图1为无谐振峰减振系统的抽象模型[2]。图中,m为晶体振荡器的质量;k为减振器的劲度系数;Fμ为干摩擦力;z、ze分别为晶体振荡器和基座的位移。该模型的运动微分方程可表示为

(1)
式中,λ=±1是取决于质量与基础相对速度的符号函数。
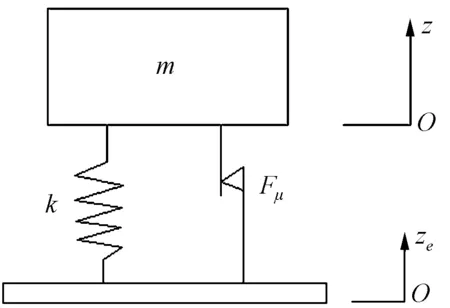
图1 库仑阻尼系统
由非粘性阻尼的能量等效原理可知,库伦阻尼可等效为粘性阻尼,其等效粘性阻尼系数为
(2)
式中:μ为干摩擦阻尼系数;N为正压力;p为激励频率;B为阻尼力在一个周期中的振幅。
如将干摩擦力等效为粘性阻尼,则式(1)可改写为

令ze(t)=A0eipt,u=z-ze,则有
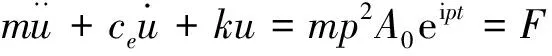
若z=Bsin(pt-θ),则有传递率:
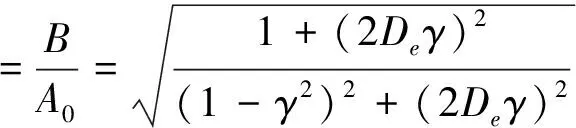
(3)
式中:θ为滞后相位角;γ为频率比;De=ce/cc为等效阻尼比,即粘性阻尼与系统临界阻尼的比。

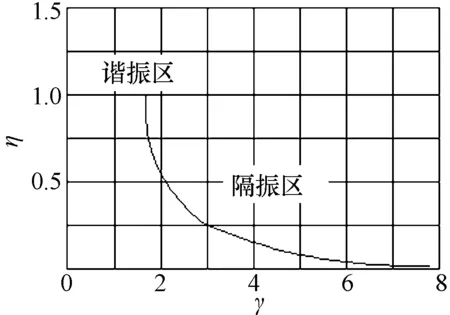
图2 无谐振峰传递率曲线
2 减振系统结构设计
2.1 布局设计
传统的无谐振峰减振器通常将隔振体安装在盒内,压簧和隔振体四周安装簧片,利用簧片与盒内壁的干摩擦来实现无谐振峰隔振。此设计如运用在晶振减振上,则对整个减振系统的重量、空间、后续的维护性要求有很大的挑战。本文全面考虑这些问题,设计了一个专用的隔振缓冲系统,如图3所示。

图3 晶振减振系统结构图
晶振“架”在框架中间,框架底部与模块连接,框架四角用了8根钢丝绳,其中4根作为限位装置,起导向与摩擦作用;另外4根制作成环形,一端与底部固定,环形端连接晶振,将晶振“架”空。
鉴于单质体多自由度系统一个方向的振动必然会引起另一个方向的振动,为了使该单质体质量重心与刚度中心重合,从而不引起耦合振动[2],在晶振四周对称安装环形钢丝绳,晶振上加装锁紧盖帽,将减振器重心尽量调整到系统中心平面内。由此,减振系统在铅直方向是非耦合运动,水平方向也基本符合非耦合布置条件。
2.2 减振结构的算例分析
设计无谐振峰减振器所需参数如表1所示。

表1 无谐振峰减振器输入参数
本文所使用晶振质量为50 g,体积为50 mm × 50 mm × 25 mm,外界激励的最低频率为20 Hz,晶振相位噪声动态相对静态恶化指标:随机振动条件40 dBc/Hz @100Hz内;正弦加随机振动条件50 dBc/Hz @100Hz内。
首先为了避开共振区域,减振系统的固有频率至少应设定为
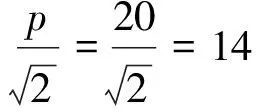
本次设计所需的钢丝绳泊松比为0.34,密度7.8 g/cm3,直径1.8 mm,钢丝绳内部结构阻尼比0.15,由

可知k≤394 264.9 N/m,带入公式:
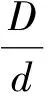

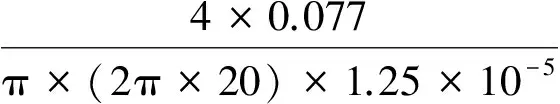

当条件为随机振动f=20Hz,加速度功率谱密度为0.202 g2/Hz时,由式(3)可得系统隔振率η≈0.73。此时,晶振将一直处于隔振区。此后随着激励频率的增加,γ值越来越大,系统的隔振传递率将逐渐降低,从而进一步保证晶振在中、高频处频率的稳定度。
对该减振系统在随机振动、正弦加随机振动100Hz处进行理论分析,发现结果满足实际的指标要求。
如不要求晶振时刻处在隔振区内,可从晶振相位噪声恶化指标考虑,分析共振区的影响是否满足要求。鉴于本文晶振在雷达上有很高的可靠性要求,故直接从隔振区考虑。
3 实验研究
所选晶振中心频率为120MHz。为了测试该减振系统的效果,进行了两种条件下的实验,并与橡胶减振器进行了对比。
3.1 试验对比输入条件
该试验采用:(1)随机振动,加速度功率谱密度参数见表2,功能试验时间30min。(2)正弦加随机振动,加速度功率谱密度见图4,试验持续时间每个轴向为1h。

表2 随机振动加速度功率谱密度

f1=20 Hz; A1=2.97g; f2=39.6 Hz;A2=3.75g; f3=59.4 Hz;A3=2.25g; f4=79.2 Hz; A4=2.25g;W0=0.005 g2/Hz;W1=0.04 g2/Hz; ft=500 Hz图4 正弦加随机振动加速度功率谱密度
针对该减振器,分别做了高低温环境下的振动试验,并与两种结构的航空橡胶板减振器进行了对比。
3.2 试验对比标准
1981年,Raymond L. Filler研究了振动环境对晶体振荡器输出频率造成的影响[4]。在单方向上的单一频率振动环境下,晶体振荡器的输出频率:
f(t)=f0〔1+SgA(t)〕
式中:f0为晶体振荡器静止状态的输出频率;Sg为晶体振荡器的加速度灵敏度;A(t)为振动的瞬时加速度。此种情况下,由振动引起的相位噪声可近似表达为
式中:fv为振动频率;Ap为振动的加速度,g。
多数情况下,晶体振荡器处于随机振动环境中,加速度可用其功率谱密度函数G(fv) 表示,此时晶体振荡器的相位噪声为
3.3 试验对比结果
晶体振荡器输出的电信号在各个频率点下相位噪声结果见表3~表6。
表3 20 ℃下随机振动条件下晶体振荡器的相位噪声 dBc/Hz

减振器0.1kHz无振动有振动1kHz无振动有振动2kHz无振动有振动10kHz无振动有振动钢丝绳-87-52-99-96-108-107-114-114航空橡胶板(底部安装结构)-87-63-99-98-108-108-114-114航空橡胶板(四周拉接结构)-87-63-99-99-108-108-114-114
表4 -55 ℃下随机振动条件下晶体振荡器的相位噪声 dBc/Hz

减振器0.1kHz无振动有振动1kHz无振动有振动2kHz无振动有振动10kHz无振动有振动钢丝绳-85-50-97-96-108-108-114-114航空橡胶板(底部安装结构)-85-32-97-94-108-107-114-114航空橡胶板(四周拉接结构)-85-32-97-94-108-107-114-114
表5 20 ℃下正弦加随机振动条件下晶体振荡器的相位噪声 dBc/Hz

减振器0.1kHz无振动有振动1kHz无振动有振动2kHz无振动有振动10kHz无振动有振动钢丝绳-87-41-99-94-108-107-114-114航空橡胶板(底部安装结构)-87-45-99-96-108-108-114-114航空橡胶板(四周拉接结构)-87-44-99-96-108-108-114-114
表6 -55 ℃下正弦加随机振动条件下晶体振荡器的相位噪声 dBc/Hz

减振器0.1kHz无振动有振动1kHz无振动有振动2kHz无振动有振动10kHz无振动有振动钢丝绳-85-38-97-90-108-107-114-114航空橡胶板(底部安装结构)-85-29-97-85-108-106-114-114航空橡胶板(四周拉接结构)-85-30-97-85-108-106-114-114
3.4 试验对比结论
1)不同振动条件下,减振器对晶振输出信号的影响在频率近端(100 Hz附近)较大,远端(1 000 Hz以上)很小。
2)在低温条件下,钢丝绳减振器对晶振的减振效果好于航空橡胶板减振器,在晶振输出信号功率谱近端100 Hz处相位噪声高出9~18 dBc/Hz。在常温下,钢丝绳减振性能则低于航空橡胶板减振器,100 Hz处相位噪声低3~11 dBc/Hz,原因是橡胶材料在常温下弹性性能很好,而钢丝绳弹性性能较差。
3)钢丝绳减振器比较适合宽温度环境,特别是在低温环境下能够保持较高的稳定性。
4 结束语
基于无谐振峰减振原理,针对电子产品晶体振荡器设计开发了无谐振峰减振系统。该无谐振峰钢丝绳减振器相对已有的减振器质量更轻、空间更小,采用非线性弹簧和非线性阻尼器等非线性元素降低了系统的固有频率,提升了低频特性以及隔振传递率。通过试验对比,在频率为20~2 000 Hz的随机振动以及20~500 Hz的正弦加随机振动条件下,特别是在低温-55 ℃环境下,该减振系统可有效降低由振动环境引起的晶体振荡器的相位噪声,在常温时减振性能与橡胶减振器相近,低温时减振性能优于橡胶减振器。
[1] SPENCER W J, SMITH W L. Precision crystal frequency standards[C]//15th Annual Symposium on Frequency Control, 1961: 139-155.
[2] 邱成悌, 赵惇殳, 蒋全兴. 电子设备结构设计原理[M]. 南京: 东南大学出版社, 2005: 147-150, 177-188.
[3] 陈维民, 刘刚, 刘玉兰. 环形钢丝绳减振器刚度和阻尼性能试验研究[J]. 材料科学与工艺, 1996(1): 70-75.
[4] FILLER R L. The effect of vibration on frequency standards and clocks[C]//35th Annual Symposium on Frequency Control, 1981: 31-39.
冯永平(1989-),男,硕士,主要从事电子设备结构设计工作。
帅立国(1968-),男,博士生导师,主要从事触觉系统以及物联网的研究。
钟剑锋(1967-),男,研究员级高级工程师,主要从事雷达大型阵面结构、微波及T/R组件结构研究。
刘国维(1971-),男,高级工程师,主要从事电子设备结构设计工作。
Applicaiton of Vibration Isolator without Resonance Peak to Radar Crystal Oscillator
FENG Yong-ping1,SHUAI Li-guo1,ZHONG Jian-feng2,LIU Guo-wei2
(1.MechanicalEngineeringCollege,SoutheastUniversity,Nanjing211189,China;2.NanjingResearchInstituteofElectronicsTechnology,Nanjing210039,China)
In this paper, the influence of vibrations on radar crystal oscillator is analyzed. Based on the analysis results, a lightweight wire-rope vibration isolator which has no resonance peak is presented and is compared with a rubber damper. Experimental results show that with the premise of good damping effect, the wire-rope vibration isolator is more suitable for using in low temperature, the phase noise level of the crystal oscillator could be 9~18 dBc/Hz @100Hz higher comparing with the rubber damper. It can be used under the conditions of ground, aircraft, ship, balloon etc. and under wide range temperatures.
crystal oscillator; wire-rope vibration isolator; light weight; phase noise; low temperature
2013-03-13
TB535;O328
A
1008-5300(2013)03-0001-04

