CFRP薄壁管空间伸展臂模态与影响参数分析及试验

刘 靖，周 伟

（长安大学 公路学院，陕西 西安 710064）

复合材料以其高比强度、高比刚度、高尺寸稳定性和超低热胀系数等优点，在航空、航天等众多领域得到广泛应用.透镜式碳纤维增强复合材料（CFRP）薄壁管是一种基本的空间可展构件，其具有展开原理简单、轻质、可重复性精度高等特点，可用于空间可展抛物面索网天线支撑肋、平面阵面支撑框架、探测臂等[1－2].美国国家航空航天局（NASA）等成功研制径向肋、缠绕肋、盘绕式伸展臂等空间可展结构[3].日本宇航开发局（JAXA）研制出天线反射面、苜蓿花形和扇形薄膜太阳帆、三棱柱和六棱柱单元构架式展开天线[4].欧洲宇航防务集团（EADS）亦根据其特定宇航计划而研制了多种空间展开结构.德国宇航中心（DLR）研制了高性能大型CFRP薄壁管空间伸展臂[5－6].

我国在20世纪90年代初期，开展对空间可展结构的研究，并取得了一些技术成果[1，7－8]，对空间可展结构分析理论、概念模型与样机技术等有突破性进展.文献[7]对CFRP薄壁管压扁和缠绕过程进行了数值模拟研究，文献[8]对CFRP薄壁管缠绕过程的力学行为特性进行了试验及分析研究.

本文依据复合材料力学理论和试验分别计算出材料整体弹性模量，并利用数值计算方法计算了CFRP薄壁管伸展臂的自振频率，并进行试验验证，进而对影响自振特性的结构参数进行研究.

1 材料试验及弹性模量计算

1.1 材料试验与实测弹性模量

薄壁管采用环氧树脂碳纤维增强复合材料4层（45°／-45°／45°／-45°）铺设，每层厚度为0.1mm.分别取纵向和横向试件进行试验，每根薄壁管的长L＝300mm，宽B＝30mm，厚H＝0.4mm，有效长度L0＝200mm，制作误差均小于1mm，如图1所示.

图1 肋片试件Fig.1 Test specimens

试验在常温正常环境下进行，试件被恒速拉伸直至破坏，夹具移动速度为200mm／min.试验设备采用CHA-20kN型拉伸强度试验仪.假设3个试件编号为L1～L3.

测得试件拉伸力－位移曲线，计算开始弹性阶段的弹性模量，通过计算转换为应力－应变关系如图2所示，使用最小二乘法对试件L1～L3的试验值进行线性拟合，利用直线斜率计算弹性模量，并取3个试件的平均值.由于材料4层（45°／-45°／45°／-45°）铺设，纵向和横向弹性模量应该相等，计算出试件的整体拉伸弹性模量为E11＝E22＝35.8GPa.E11和E22表示层合整体弹性模量.

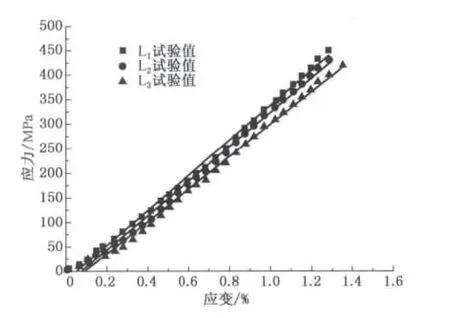
图2 CFRP薄壁管试件的拉伸应力－应变曲线Fig.2 Stress-strain curves of the CFRP thin-walled tubes

1.2 理论计算弹性模量

根据单层碳纤维预浸料材料参数，由复合材料力学理论计算出整体材料参数[9].

1.2.1 单层碳纤维复合材料的本构

单层碳纤维复合材料应力－应变关系式为

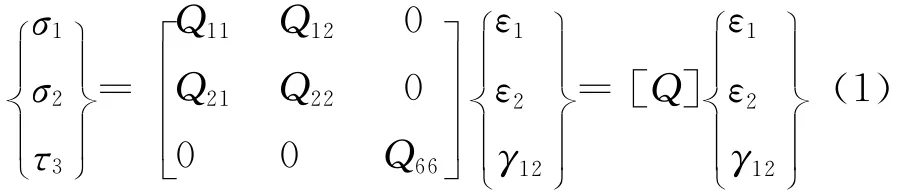
[Q]为折减刚度矩阵，它的元素为

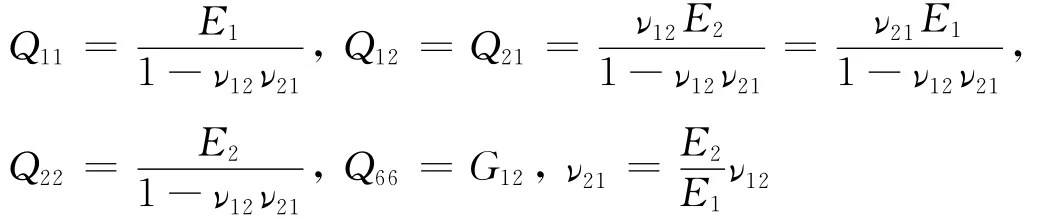
式中：E1和E2分别为单层碳纤维板沿纤维方向和垂直纤维方向的弹性模量；ν12和ν21分别为各向异性材料两个方向的泊松比；G12为单层碳纤维剪切模量；σ和ε分别为各向异性材料的应力和应变；τ3和γ12分别为各向异性材料的剪应力和剪应变.

当单层复合材料主向坐标系与自然坐标系间有夹角θ时，得到转换折算刚度矩阵为

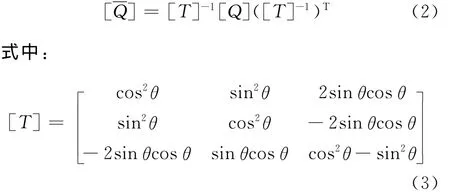
1.2.2 2N层反对称角铺设层合复合材料的本构

单位宽度复合材料的内力－应变关系式[9]为

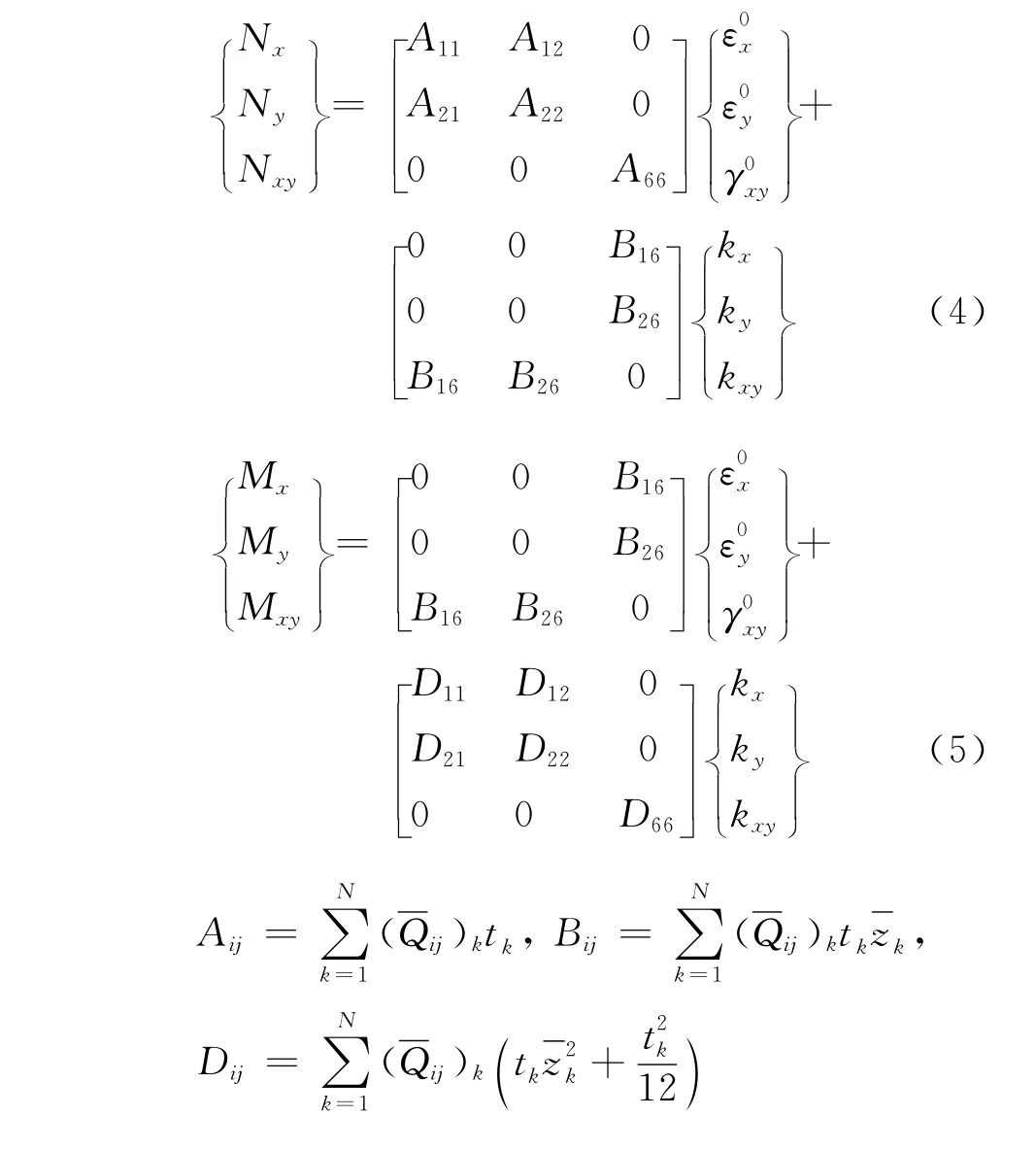
式中：Aij，Bij，Dij依次为拉伸刚度、耦合刚度、弯曲刚度；tk为第k层的厚度为第k层中心的z坐标值；Nx，Ny，Nxy分别为复合材料单位宽度两个方向轴力和面内剪力；Mx，My，Mxy分别为复合材料单位宽度两个方向弯矩和面内扭矩表示相应折减刚度矩阵.

4层（45°／-45°／45°／-45°）环氧树脂碳纤维单层预浸料后参数：E1＝126GPa，E2＝7.2GPa，ν12＝0.3，G12＝3.6GPa，将其代入式（1），得到[Q].单层材料主向坐标系与自然坐标系间的夹角θ＝45°，将θ及[Q]代入式（2）和（3），计算各变量.

将各参数代入式（4）和（5），得A11＝A22＝15.26，B16＝B26＝－0.59，D11＝D22＝0.2，D12＝0.16，D66＝0.17，因为B和D的值都较小，可不考虑拉弯耦合效应.忽略弯曲刚度和扭转刚度，t为碳纤维4层总厚度，t＝0.4mm，得到

并将上式结果转换为45°方向，计算得到4层复合材料与自然坐标呈45°方向的整体弹性模量E11＝E22＝38.16GPa，比实测结果大6.6%.考虑到材料实际制作偶然误差、几何缺陷较大，试验结果和理论计算结果基本吻合，可用实测值作为计算分析材料的参数.

2 透镜式CFRP薄壁管空间伸展臂模态分析

采用如图3所示薄壁管建模，CFRP材料4层（45°／-45°／45°／-45°）铺设，每层厚度为0.1mm，长度为700mm.薄壁管由上、下两片通过黏结胶黏结，黏结胶厚度为0.1mm.单层材料参数：E1＝126GPa，E2＝7.2GPa，ν12＝0.3，G12＝3.6GPa，ρ＝1 600 kg／m3.空间伸展臂假设为一端固定悬臂梁.

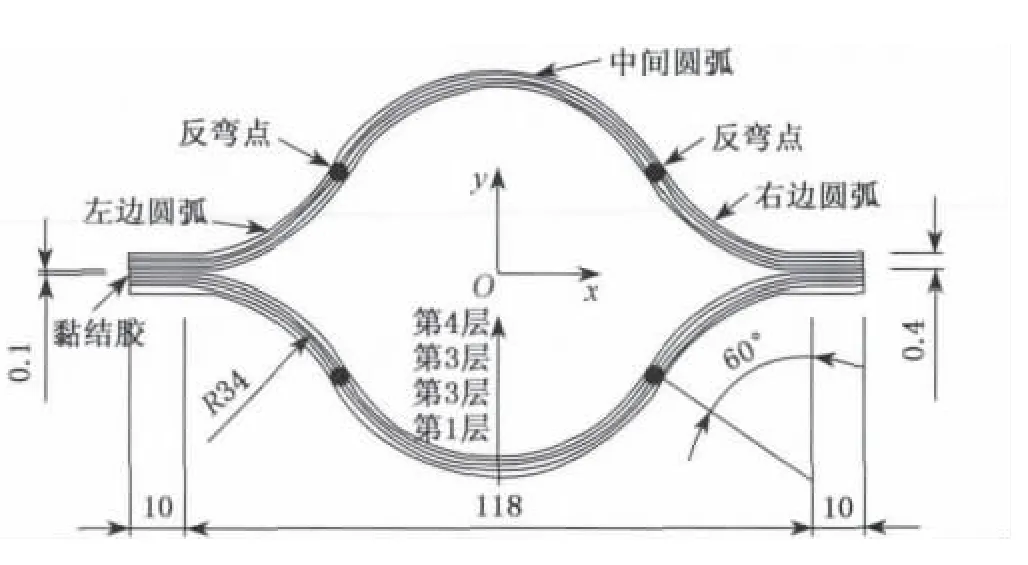
图3 薄壁管截面（单位：mm）Fig.3 Thin-walled cross-section（unit：mm）

伸展臂由上、下两片在边缘黏结而成，单片由4层组成，各层纤维方向以-45°／45°布置，单片截面定义如图4所示.

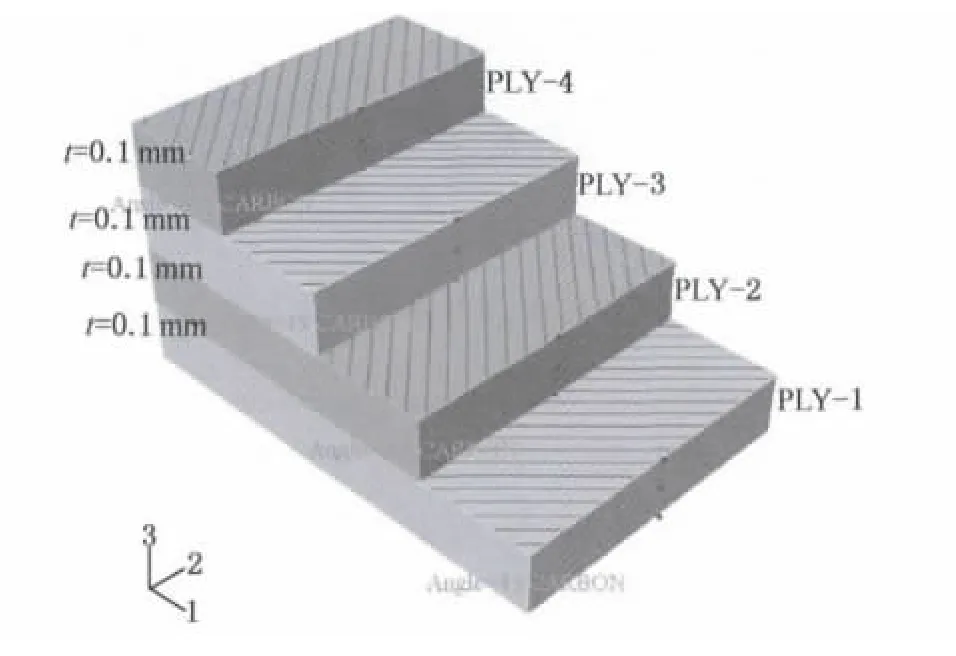
图4 CFRP薄壁管各层材料铺设布置Fig.4 Lay-up of CFRP thin-walled tube

利用ABAQUS对CFRP薄壁管建立有限元模型，单层采用以上材料参数，整体是薄壁壳结构，采用壳单元S4R（4节点1次减缩积分）划分有限元网格进行模态分析，上、下片之间黏结胶采用cohesive单元模拟.采用分块兰索斯法（Block-Lanczos）[10]求解模态.

计算分析得到前5阶频率分别为63.94，109.28，119.43，175.95，201.16Hz.第1阶模态为弯曲型，如图5所示.由于伸展臂长度较短，截面薄壁中空，其他阶模态均发生局部振动，而非整体弯曲.

图5 第1阶模态Fig.5 The first mode

利用第1节计算得到的层合整体弹性模量为参数进行数值计算，材料采用各向异性参数一层建模，边界条件及计算方法与前面相同，得到第1阶频率为58.9Hz，模态为弯曲型，与分层参数输入计算结果一致，因此，数值计算时可利用复合材料单层参数或者整体参数进行模态计算.

3 透镜式CFRP薄壁管空间伸展臂模态试验

为了得到空间伸展臂的自振频率和模态，采用CFRP材料4层（45°／-45°／45°／-45°）铺设，每层厚为0.1mm，长为700mm，取3个试件进行了试验，截面如图3所示，薄壁管伸展臂及夹具如图6所示.

图6 CFRP薄壁管伸展臂及端夹具Fig.6 CFRP thin-walled space boom and end clamping device

用预先制作的夹具固定伸展臂的一端，保持水平悬臂状，并将夹具与地面装置固定.采用德国polytec激光扫描测振系统，测试前采用polytec测振系统建模，划分几何网格，共设置5行9列共45个测点，在每个测点粘贴表面反光纸用于反射激光，并使用激光精确定位，调整激光束与各个测点一一对应.测点布置如图7所示.

图7 测点布置图Fig.7 Measure points lay-out

这里分别采用声波激振和激振器激振进行模态测试.声波激励和激振器激励都使用正弦曲线能量输入，激光测试系统及激励如图8所示.其中，polytec激光测振仪是整个测试系统的核心部分，由激励系统输入能量进行激励，采用激光扫描测振.自振频率、模态采用每个点测试3次取其平均值，再取全部测点的平均值.

图8 激光测振系统Fig.8 System of laser vibrometer

在实际测试时，要使敏感元件振动起来，并且保证其振动幅度能被检测出来，必须保证激励信号在要求的频带内有足够的功率.而且由于不同的传感器的谐振频率不同，同一个传感器也有多个谐振频率.所以在选择激励信号时，必须满足信号的功率集中于所要求的频带内，在频域上可以方便地调整信号频带所在的位置.

参考数值计算结果，调整输入能量大小，经过反复尝试发现声波激励能量输入太弱，测出结果不理想，所以进一步使用激振器激励进行测试.激振器激励位置可在根部、中部和端部，由于激振器本身的摩擦等阻力对模态测试有影响，经过各个位置测试结果发现，在根部激励时符合悬臂梁本身振动特征，能够得到一端固定悬臂梁第1阶频率及模态的精确结果.

测试得到前5阶频率分别为61.5，120.7，124.1，170.3，189.8Hz.采用polytecscan软件提取模态，第1阶振型为1阶弯曲型，如图9所示，与数值计算结果吻合.由于高阶频率均发生局部振动，测点布置较少导致测试误差较大，第2频率比数值计算结果大10.5%，第5阶频率比数值计算结果小5.6%.通过细化网格，增加测点数，调整激励位置，能够较精确地测试出有局部振动的振型.

图9 伸展臂第1阶振型Fig.9 The first mode of space boom

4 频率影响参数分析

由于伸展臂自振特性对其缠绕、展开过程及工作状态有很大影响，而薄壁管自身材料参数、截面形状、密度、长度对其自振频率都产生影响，这在一定程度决定了空间可展结构可实现的几何尺寸和工作形态.基于第2节的分析方法和定义的特征截面、单元，这里进行伸展臂截面形状、材料参数分析，评价其对自振频率的影响，包括线刚度（EI／L）和刚度线密度比（刚度与单位长度质量比，EI／m）对自振频率的影响.其中，E为第1节计算得到沿管轴的复合材料整体弹性模量，I为图3薄壁截面对x轴的惯性矩，m为单位长度质量，L为长度.

4.1 伸展臂线刚度（EI／L）对自振频率的影响

采用图3所示截面，CFRP材料4层（45°／-45°／45°／-45°）铺设，厚度为0.4mm，分别进行了伸展臂长度为0.7～50m模态数值模拟分析，材料参数、模型及边界条件同第2节.伸展臂的第1，3，5阶振型都为弯曲型，下文仅取此3阶频率进行研究.

空间伸展臂自振频率随长度的变化如图10所示.当臂长小于10m时，第1，3，5阶频率随长度增加显著降低，长度对频率影响敏感；当臂长大于10m时，频率变化较平缓；当臂长超过30m时对频率的影响很小.空间伸展臂线刚度对频率的影响如图11所示，随着线刚度增大，频率基本呈抛物线型增加，对第3和5阶高频频率的影响较明显.

图10 伸展臂长度对频率的影响Fig.10 The space boom length effect on frequency

4.2 伸展臂刚度线密度比（EI／m）对自振频率的影响

采用图3所示截面，CFRP材料4层（45°／-45°／45°／-45°）铺设，厚度为0.4mm，臂长为700mm，EI与上文相同，分别进行了不同密度情况下数值模拟分析，并转化为EI／m与频率的关系，材料参数、模型及边界条件同第2节.

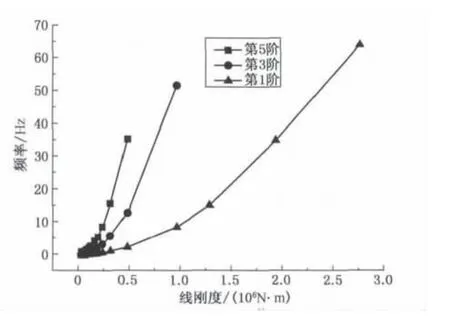
图11 伸展臂线刚度（EI／L）对自振频率的影响Fig.11 The linear stiffness of space boom effect on frequency

伸展臂的第1，3，5阶频率随EI／m的变化关系曲线如图12所示，随着EI／m增加，频率呈曲线增加，但对频率的影响逐渐减弱.与图11比较发现，刚度线密度比（EI／m）对不同阶频率的影响没有线刚度明显.

图12 伸展臂刚度线密度比（EI／m）对频率的影响Fig.12 The stiffness to linear mass ratio of space boom effects on frequency

5 结 语

本文根据单层碳纤维预浸料试验参数，按照复合材料力学理论计算出 CFRP材料4层（45°／-45°／45°／-45°）铺设情况下的整体弹性模量，结果与实测弹性模量一致，由此可知，材料分层参数和整体参数均可用于数值计算模态材料参数.

通过伸展臂自振模态试验，测得自振频率和振型与数值模拟结果吻合，验证了CFRP薄壁管伸展臂自振模态数值分析时可采用单层材料参数和整体参数，得到可行的试验测试方法和计算方法，进一步分析得到伸展臂线刚度（EI／L）、刚度线密度比（EI／m）对频率的影响，研究结果为伸展臂合理设计提供指导.

参 考 文 献

[1]陈务军.空间可展结构体系与分析导论[M].北京：中国宇航出版社，2006：10-75.

[2]MURPHEY T W.Historical perspectives on the development of deployable reflectors[C]／／The 50th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference.Palm Springs，California.2009.

[3]SOYKASAP O， WATT A M.New deployable reflector concept[C]／／The 47th AIAA／ ASME／ASCE／AHS／ ASC Structures，Structural Dynamics and Materials Conference.Palm Springs，California，2004.

[4]TANAKA H.Design optimization studies for large scale contoured beam deployable satellite antennas [J]. Acta Astronautica，2006，58（9）：443-451.

[5]GAN W W，PELLEGRINO S A.Numerical approach to the kinematic analysis of deployable structures forming a closed loop [J]. Mechanical Engineering Science， 2006，220（7）：1045-1056.

[6]PELLEGRINO S，GUEST S D.Symposium on deployable structures：Theory and applications[J].Solid and Structures，1998，80（9）：211-220.

[7]戈冬明.盘绕式空间可展伸展臂屈曲机理和结构动力分析[D].上海：上海交通大学船舶海洋与建筑工程学院，2007.

[8]李瑞雄，陈务军，付功义，等.透镜式缠绕肋压扁缠绕过程数值模拟分析[J].宇航学报，2011，32（1）：224-231.

[9]沈观林.复合材料力学[M].北京：清华大学出版社，2006：21-110.

[10]魏志刚，汤文成.复合材料网格结构模态分析的均匀化等效建模[J].复合材料学报，2008，25（2）：188-193.