电动汽车电池测试系统建模与仿真

俞 聪，姚 维，王子敬

(浙江大学电气工程学院，浙江杭州310027)

0 引 言

随着全球经济的高速发展以及能源环保等问题的日益突出，传统的内燃机汽车已经无法满足节约能源、绿色环保的要求，电动汽车以零排放和低噪声等优点已成为节能环保汽车发展的主要方向之一［1］。

然而电动汽车的发展才刚刚起步，还有很多问题亟待解决。众所周知，变频器驱动三相异步电机时，由于变频器中功率元件的开关、电机的换向等会对直流侧电流造成影响，产生较大的电流谐波。电动汽车中的驱动器与通用的变频器不一样，其直流电直接由电池提供，若不加以抑制和预防，谐波会导致电池放电不均匀，对电池寿命及发热造成影响。

电路中的滤波电路可抑制电流的谐波，故本研究搭建一个电池测试平台来测试最佳电感电容组合，以及不同种类的电容对谐波的抑制效果［2］。由于实际的测试中需要频繁地更换电容电感，测试耗时耗力，本研究在Simulink下搭建测试系统模型，可以快速地观测电感电容值以及载波频率的选取对谐波的影响。

1 系统整体模型

实验室中的电池测试系统由电池组、电感、驱动变频器和负载变频器及电机组成。电池组由100节3.2 V的锂电池串联而成;驱动侧变频器直接由电池组供电，其回路上可以串接不同电感值的电感，驱动侧变频器的母线支撑电容可以选择电解电容或者薄膜电容;负载侧变频器通过PWM Converter连接到电网上，能够将测试过程中的电能回馈到电网上，通过对负载变频器的负载率设定为驱动电机加载。

测试系统采用电流探头和示波器观测直流母线上电流，选用LeCroy公司的104MXs示波器，该示波器自带FFT分析功能，可以对直流母线电流进行FFT分析，以便与模型中的仿真数据对比。

本研究参照实际系统在Simulink下搭建了一个仿真模型，系统模型如图1所示，与实际系统不同的是，模型中的负载是通过LOAD值直接给定的，这个值可以通过实际变频器中的负载给定值计算得到。该模型通过示波器记录直流母线波形，同时以数组的形式将波形数据保存在工作空间中以便进行FFT分析。

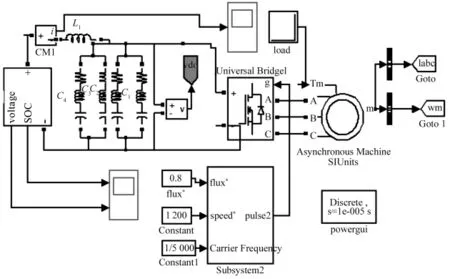
图1 系统模型

2 电池的等效电路模型

2.1 常见等效电路模型选择

等效电路模型比较直观，容易理解，且参数辨识比较方便，因此本研究选用等效电路模型。常见的等效电路模型主要有一阶Thevenin模型、PNGV模型、二阶RC模型［3］。具体介绍如下:

图2 Thevenin模型和PNGV模型

(1)Thevenin模型，也称为一阶RC模型，含一个电压源和一个RC并联电路，该模型如图2(a)所示。RS和Cs构成的回路用来模拟电池的动态过程，这种模型考虑到了电动势与SOC的关系和电池的动态过程，可较为准确地模拟电池充放电过程，因此被广泛应用在动力电池的建模中［4］。

(2)PNGV等效电路模型是美国新一代汽车合作计划(PNGV，Partnership for a New Generation of Vehicles)在2001年提出的。该模型如图2(b)所示，PNGV模型在Thevenin模型的基础上增加了一个电容Cp用来描述负载电流的时间累计产生的开路电压变化。PNGV模型对处理器要求不高且容易实现，比较适合模拟电池的动态性能，不适合对电池的长时间稳定充放电仿真。

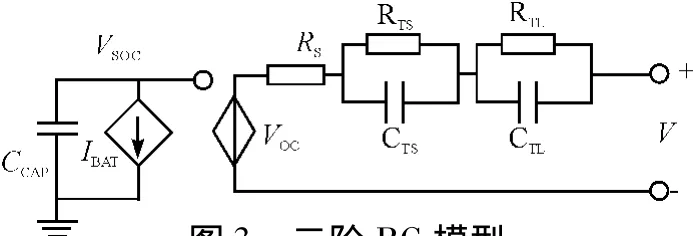
图3 二阶RC模型

(3)二阶RC模型，本研究在Thevenin模型的基础上再增加一组RC回路，组成二阶RC等效电路模型，在该模型中，这两个电路靠一个可控电压源联系在一起，左边电路表示电池的容量，右边电路通过一个串联电阻和两个RC电路表示电池的内部电阻和瞬态响应。二阶RC模型如图3所示。综上所述，二阶RC模型能很好地兼顾电池的稳态特性和暂态特性，因此该系统选用二阶RC模型。

2.2 二阶RC模型及其参数辨识

如图3所示，将两个电路联系在一起的可控电压源表征的是电池的SOC和开路电压之间的非线性关系。因为模型并不用来仿真长时间工作的情况，二阶RC模型中并没有包含自放电电阻，另外，该模型中也没有考虑温度对电池的影响。

依据电路图，研究者可以写出描述电路的常微分方程，进而可以写出模型的状态空间模型:

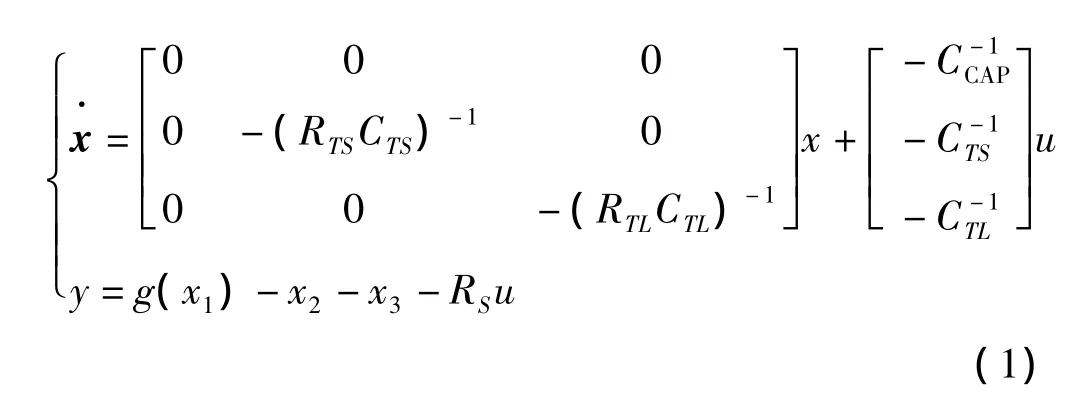
式中:RS—串联电阻;RTS，CTS—短时间(Shorter Time)RC电路;RLS，CLS—长时间(Longer Time)RC电路;CCAP—电池的容量。

设SOC为状态变量x1，RTS两端的电压为状态变量x2，RTL两端的电压为状态变量x3，系统输入u代表电池的放电电流，系统输出y表示电池的输出端电压，g(x)表示SOC与开路电压之间的非线性关系。

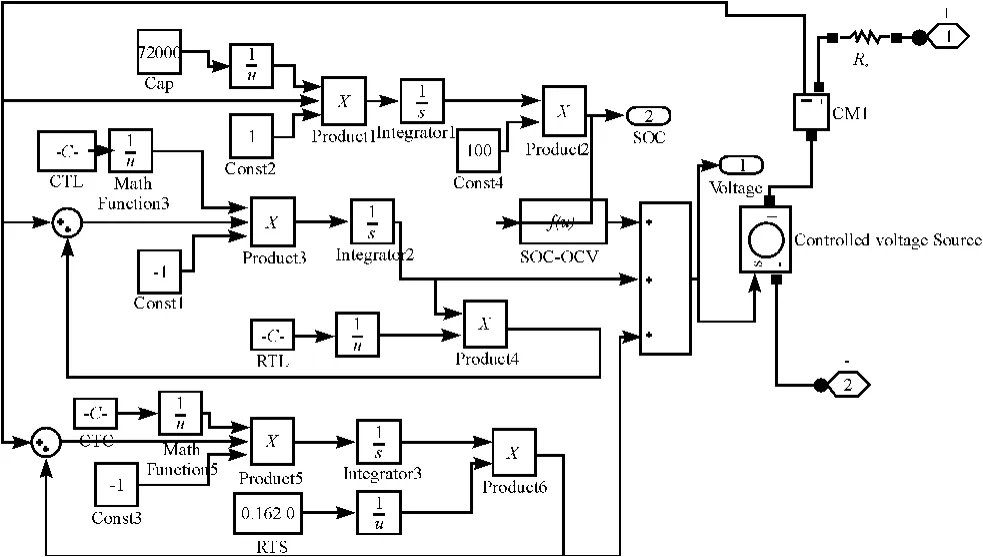
图4 最终电池模型

依据上面的状态空间模型，可以在Simulink中搭建电池模型，最终电池模型如图4所示。

2.2.1 开路电压与SOC的关系

电池的开路电压是指电池与充、放电回路断开后电压最终到达的稳定值。开路电压表征了电池在某一SOC下所对应的电动势，是一个对电池状况有着较强描述能力的状态量，提高开路电压的精度能够完善电池模型，因此，通过设计合理的实验方法以获取准确的开路电压十分重要。

本研究用两种不同的放电倍率，将电池恒流放电至SOC为0。利用获得的两条电池电压曲线。依据等效电路的原理图，可以得到电池开路电压的计算公式，如下式所示:

UIn和Ulm都是可以通过实验获得的量，因此可以根据上面两式将Uoc和∑R求出，其结果如下:

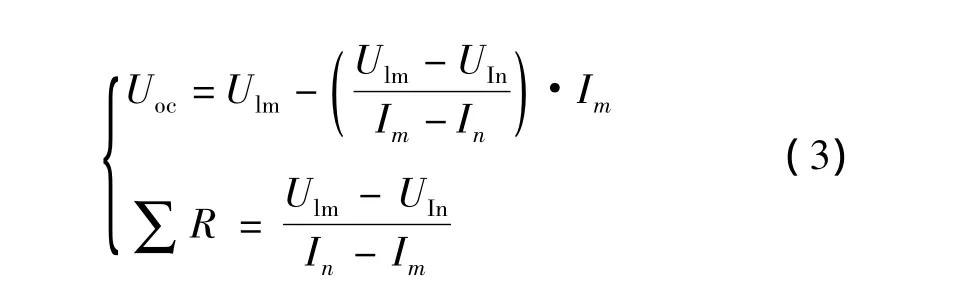
该实验采用恒流放电的得到不同放电倍率下两条电池端电压曲线，开始放电时认为放电深度为0，放电结束时为100，笔者在每条放电曲线中各取等间隔的100个点作为电池端电压，并计算出开路电压。

通过观察曲线的形状，参照已有论文中的模型，并通过比较各个不同非线性关系表达式的拟合效果，最后得出开路电压与SOC之间的非线性关系，如下式所示［5］:

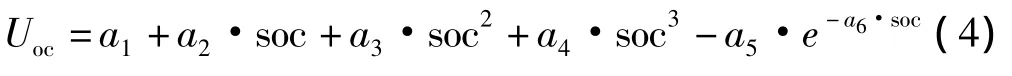
本研究利用非线性最小二乘原理，对曲线进行拟合，即可得到对应的参数，通过调用Matlab的lsqcurvefit函数实现。其拟合的曲线和实际曲线如图5(a)所示。为更清晰地分析其拟合效果，笔者将实际曲线与拟合曲线的误差绘制成曲线，如图5(b)所示。

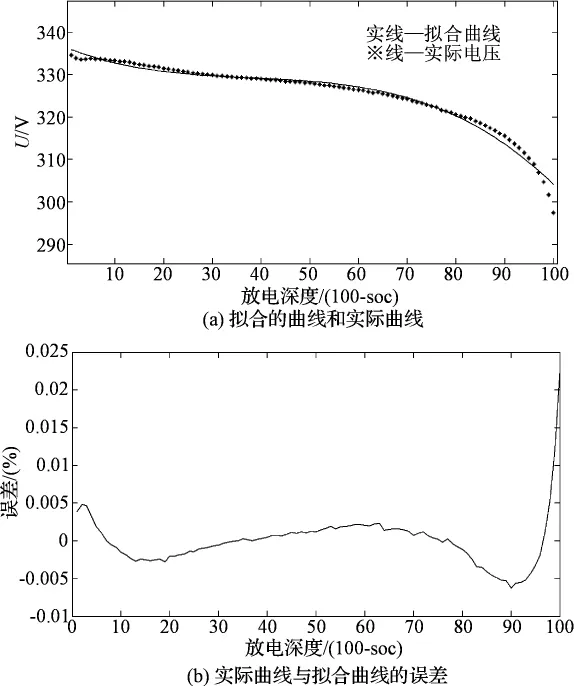
图5 开路电压与SOC的拟合曲线及误差

2.2.2 RC 参数辨识

模型中的并联RC电路主要是为了模拟锂电池的动态特性，因此本研究必须给电池以动态的电流刺激才能得到与RC参数相关的实验数据。目前，应用最广泛的方法就是脉冲实验法［6］。由电路知识可知，电池端电压的函数关系式如下:

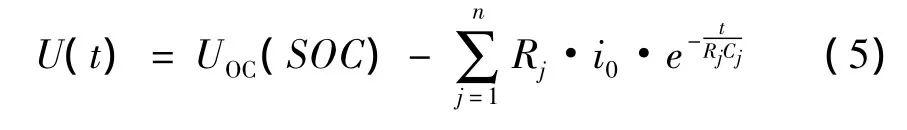
实验开始时电池以20 A恒流放电，在某一时刻突然断开负载，记录电池端电压的恢复过程。系统每秒采样一次，将数据和上面的函数关系式导入Matlab，调用lsqcurvefit函数进行曲线拟合，便可得到二阶RC电路的RC参数。

3 电机驱动建模

该系统采用的是三相交流感应电机，采用矢量控制方式，因此模型中也采用相同的控制方式，即SVPWM控制策略。

电压空间矢量PWM(SVPWM)控制策略是依据变流器空间电压矢量切换来控制变流器的一种新的控制策略［7-8］。空间矢量控制策略早期由日本学者在20世纪80年代初针对交流电动机变频驱动而提出，其主要思路在于抛弃了原有的正弦波脉宽调制(SPWM)，而是采用逆变器空间矢量的切换来获得准圆形旋转磁场，从而在不高的开关频率下，使交流电机获得了较SPWM 控制更好的性能［9］。

电机驱动模型如图6所示，整个模型采用双闭环的结构，内环为电流环，外环为速度环。

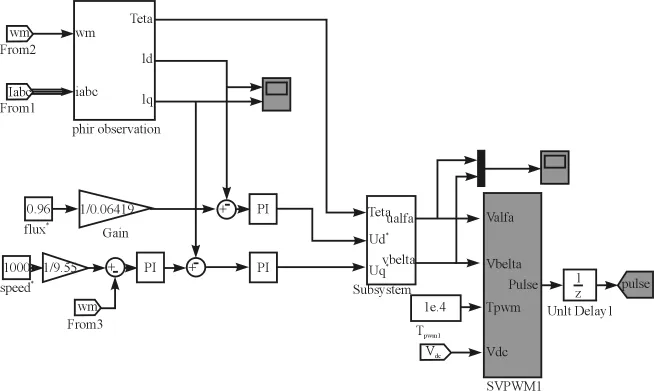
图6 电机驱动模型

电机的转速经反馈后与给定转速进行比较，其差值经过PI调节作为q轴电流的给定值，而d轴电流的给定值是根据d轴电流与给定磁链的关系计算得到的，此时的两个给定值再与由磁通观测器计算所得的实际值进行比较，这两个差值经过PI调节后即可得到Ud、Uq的给定值，再经过SVPWM的变换获得6个IGBT的触发信号控制逆变输出的电压值［10］。

4 模型的验证

本研究将开路电压与SOC的关系曲线以及RC参数填入模型，得到电池模型。由于电池模型是以10 A和20 A放电的实验数据下建立的，为验证模型的精确性，系统测试15 A放电时的电池电压变化曲线，并对比其误差，对比结果如图7所示。由图7可以看出，除了在SOC低于10或高于90的两端外，中间段电池误差基本为0。而用在分析谐波的电池电量一般不是在SOC过高或过低情况下，因此模型可用。

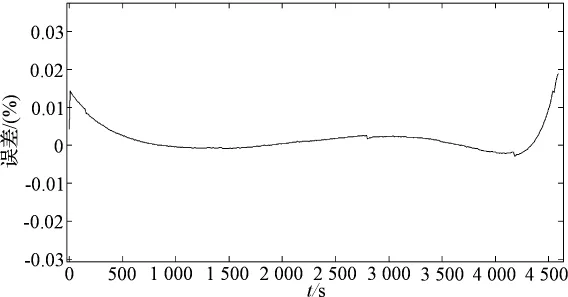
图7 模型误差

最终电池模型是用在分析电流谐波上的，因此在系统模型中，本研究通过电流谐波的FFT分析与实际电流的FFT分析的比较验证其正确性。以有没有电感情况下的载波频率分量比较为例，模型中数据通过示波器保存到Matlab工作空间中，再编写m文件加载这些数据并调用FFT函数对其进行FFT分析，其结果如图8、图9所示，图8、9中，左边无电感，右边有电感，仿真结果如图8 所示，载波频率分量分别为0.48 A 和0.31 A［11］。

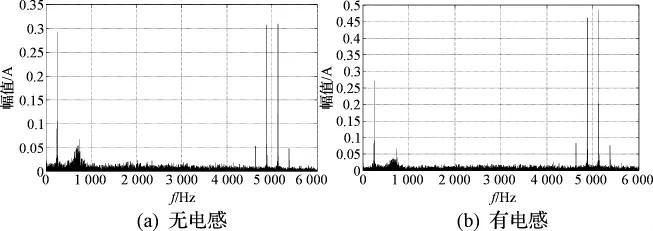
图8 仿真结果

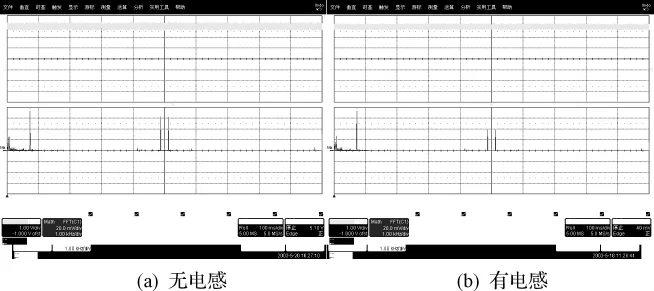
图9 实际波形及FFT分析

实际情况下示波器FFT分析的结果如图9所示，其载波频率分量分别为0.3 A和0.2 A。由于模型中电机驱动部分与实际应用中变频器不可能完全相同，控制策略也可能有所差异，存在一些误差，但电感的有无造成的影响是一致的，且在有、无电感两种情况下母线电流谐波含量比例接近，因此模型可以用来仿真实际电路确定电感电容值［12］。

5 结束语

本研究通过分析实际的放电测试实验数据，在Simulink下搭建了电池的二阶RC等效电路模型，并通过长时间放电实验和在电机负载下的谐波分析实验验证了模型的正确性，为后面的系统仿真及滤波优化奠定了基础，但是该模型在SOC过高或过低时误差偏大，尚需进一步完善。

［1］卢少武.基于永磁同步电机的电动汽车调速系统研究［D］.武汉:武汉理工大学信息工程学院，2009.

［2］杨兴辉.电动汽车驱动系统试验平台的控制研究［D］.北京:北京工业大学机电学院，2011.

［3］夏 晴.电动汽车用锂离子电池荷电状态估计算法的研究［D］.哈尔滨:哈尔滨工业大学航天学院，2011.

［4］王志贤.最优状态估计与系统辨识［M］.西安:西北工业大学出版社，2004.

［5］陈全世，林成涛.电动汽车用电池性能模型研究综述［J］.汽车技术，2005(3):1-5.

［6］CHENG Min，GABRIEL A.Accurate electrical battery model capable of predicting runtime and I-V performance［J］.IEEE Transactions on Energy Conversion，2006，21(2):504-511.

［7］邵海岳，钟志华，何莉萍，等.电动汽车动力电池模型及SOC 预测方法［J］.电源技术，2004(10):637-640.

［8］周 翔，杨 林，羌嘉曦，等.电动车用新型复合电源系统的设计［J］.机电工程技术，2012，41(3):7-11.

［9］KNAUFF M，MCLAUGHLIN J，DAFIS C，et al.Simulink Model of a Lithium-Ion Battery for the Hybrid Power System Testbed［C］//Proceedings of the ASNE Itelligent Ships Symposium.Philadelphia:［s.n.］，2007.

［10］赵仁德.变速恒频双馈风力发电机交流励磁电源研究［D］.杭州:浙江大学电气工程学院，2005.

［11］洪乃刚.电力电子和地理拖动控制系统的MATLAB仿真［M］.北京:机械工业出版社，2009.

［12］陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社，2008.