实现超长零件测量的三坐标测量机辅助设备研制及检测方法研究

陈 锋，邴智刚，李尚会，程 力，杨 翊，张治权，陈 佳

(浙江省质量检测科学研究院，浙江杭州310027)

0 引 言

在零部件的形位公差测量过程中，往往不能在同一坐标系中将零部件的形位公差一次测出，其主要原因是:产品尺寸超出测量机行程(如本研究所涉及的三坐标测量机的长度方向上的行程为750 mm，无法满足750 mm以上形位公差的测量要求，超出测量范围的工件称为超长零件，下同);测量探头不能触及产品的反面;当零部件移动后需要对产品进行重定位测量［1］。对于复杂或超出测量范围很多的零部件，测量过程中常需要多次定位测量，最终的测量数据就必须依据一定的计算方式进行多次重定位整合，把各次定位中测得的数据转换成一个公共定位基准下的测量数据，实现超长尺寸形位公差的测量。这种技术就是逆向工程，又称“反向工程”或者“反求工程”［2］。逆向工程的发展推动着测量技术的发展，也对测量技术提出了更高的要求。

国内已有一些高校在逆向工程方面进行了研究，如浙江大学李剑、单岩等［3］研发了逆向工程中三坐标测量数据处理系统，在CT复原三维模型方面开展了大量的研究工作，推出了Re-Soft软件系统;上海交通大学邢镇容［4］、尹忠慰等［5］研究了在一张自由曲面薄金属片上整体的逆向工程技术研究，提出了整体逆向工程技术的模型，提出了服从边界约束条件下的数字化点云的NURSS曲面的一种算法;华中科技大学李建军等［6］对逆向工程及其相关技术问题包括数据采集方法、坐标点的精简分割等进行了研究。此类研究以理论研究为主，主要用于小零件的形貌复现。由于所设计的装置价格高昂，测量范围限制等特点，上述研究很少应用到超长尺寸形位公差的检测中，尤其是基于三坐标测量机的超长零件检测的相关报道甚少。

本研究提出一种基于平台移动的、利用平台上的精密几何体作为基准点、采用刚性变换进行基准点测量和计算优化的检测方法，设计制造基于三坐标测量机辅助测试设备，以实现超出特定三坐标测量机量程的超长零部件的精密测量。

1 测量原理

1.1 重定位基本原理

因被测量物体的尺寸超出了测量范围而必须进行两次定位的示意图如图1所示。本研究在被测物体上选取不共线且在两次定位状态下均可测量的3个点(A、B、C)称为重定位基准点。设在第1次定位状态下测得 A、B、C 的坐标值分别为(x1，y1，z1)、(x2，y2，z2)和(x3，y3，z3)，在第2次定位状态下测得的坐标值分别为(X1，Y1，Z1)、(X2，Y2，Z2)和(X3、Y3，Z3)，通过如下的矩阵变换可将第2次定位坐标下的测量数据转换至第1次定位坐标中:

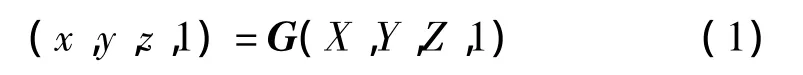
式中:G—4×4阶齐次变换矩阵，可通过A、B、C前后两次的测量结果得到。

另外3个点(D、E、F)作为辅助点存在。

如果一次移动还无法满足测量的要求，可以根据上述原理进行再次重定位。把重定位的数据进行整合，就能得到所需要的大尺寸测量的相关形位公差。

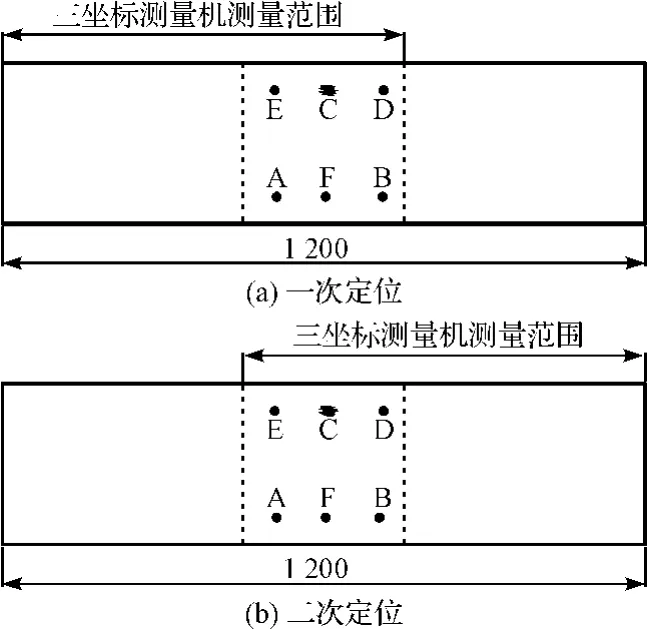
图1 再次定位示意图

1.2 超长零件测量实现原理

测量超长零件(工件)移动前后坐标值时，常采用的方法有:多次测量取平均值［7］，同线多点同面多线测量［8］等。但这些方法由于以下原因而存在着测量误差:①每次定位时需要测量同一个点，显然该操作比较困难;②受环境和测量人员视力等方面的影响，每次测量都会有一定误差;③测量机探针倾斜导致的误差，使得同一点的每次测量值会有所不同而存在误差。

工件移动前后，无法找到同一测量点，这势必影响坐标变换的精度，并最终影响测量精度。为此有学者提出了使用几何中心作为坐标变换的基准点［9］。这减少了测量的难度，即不用完全找到工件移动前的点进行测量，而只要测得几何体表面点，并进行构造几何特征点即可。

在实际测量中，被测工件上很难找到多个适用的几何体，且无法获得几何体的几何精度和几何体表面质量。鉴于以上原因，本研究不采用被测工件上的几何体特征，而采用在承载移动平台上安装高精度的几何体特征(如球心)。

本研究提出如下测量实现思路:

(1)采用移动平台作为超长零件的承载平台，利用承载平台的大量程移动来实现超长零件的长距离移动，通过移动来测量超长零件中不同部位的相关参数。

(2)在移动平台上安装6个精密标准球(其中3个球是测量基准球，两个球是检验用球，另一个球是备用球)。利用精密球良好的球度，可方便、准确地找到基准几何体特征(球心)。

(3)平台长距离移动前后，分别测量基准几何体特征，并对所测几何体特征坐标值进行修正优化变换，以实现基准点坐标值的精确测量。

(4)按照重定位整合的基本原理，利用三坐标测量机自带软件和项目设计软件相结合的方法，进行数据处理(其中，形位公差的计算通过三坐标自带软件处理，坐标变换相关数据通过项目设计软件进行处理)，实现坐标平台移动后数值的坐标变换，获得超长零件的形位公差。

2 辅助设备研制

根据测量实现原理，测试平台只需要提供承载、移动和安装重定位基准点的功能，对平台的移动无特殊要求。但考虑到计算结果的随时监控性，平台的移动方向以三坐标X方向为基准，确保平台移动过程中在Y和Z方向上实现最小量的变化。平台的移动距离为450 mm，测量范围在X方向上由原来的750 mm扩展到了1 200 mm，使长度测量范围拓宽了60%。超长零件辅助测量设备实物如图2所示，主要包括移动平台、精密基准球、导轨副和相应夹具。

图2 三坐标测量机辅助设备实物图

3 数据优化和软件设计

3.1 基本数据处理和数据校准优化

两次定位坐标变换示意图如图3所示，两次基准点按△A1B1C1、△A2B2C2测量顺序形成一一对应关系。其中 A1、B1、C1依次对应 A2、B2、C2。基准点两组测量值构成的两个三角形之间，对应边边长有相对误差。本研究设经过一顶点的两条边的相对误差为D1、D2，定义顶点精度为D=(D1+D2)/2，D越大则顶点精度越低。据此可以对顶点按精度排序。

根据上述基本数据处理，可以放弃精度比较差的测量点，但在一些特殊情况下可能出现误判。

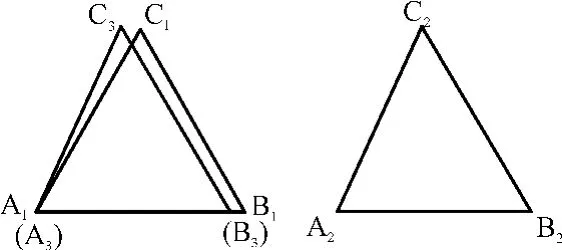
图3 两次定位坐标变换

两次定位变换示意图如图4所示，假设△A1B1C1变形到△A3B3C3，其中|A1B1|=|A3B3|，A1点精度最高，A3点相对A1点位置不变，如果C3点也相对于C1点不变，这时A3点误差为0，B3点误差为|B3C3|/2，C3点误差为|B3C3|/2。按照规定可以放弃B3点和C3点中的任意一点，但事实是，C3点的实际误差为0，这就存在着把精度较高的点放弃的概率。

又假设△A1B1C1变形到△A2B2C2，其中|A1B1|=|A2B2|，A1点精度最高，A2点相对A1点位置不变，如果C2点也相对于C1点发生如图所示变化，这时A2点误差为|C1C2|/2，B2点误差为(|B1C1|－|B2C2|)/2，C2点误差为［(|B1C1|－ |B2C2|)+|C1C2|］/2，即 C2点误差＞B2点误差＞A2点误差。按照规定可以放弃C3点。但从图上可以看出:B2点误差＞C2点误差＞A2点误差，所以存在着把精度较高的点放弃的概率。

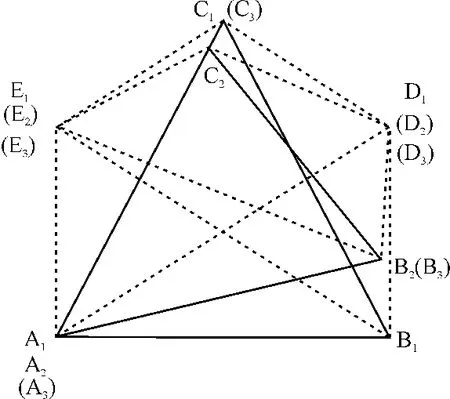
图4 两次定位变换

为了防止类似判断失误的出现，必须另加校准点，对上述情况进行查错。本研究采用近似等边三角形上的精密测量球作为基准测量球(A，B，C)。另安装两个球体(D，E)，理论上D球到A球和C球(E球到B球和C球)距离相等。利用D、E球对第2和第3精度点进行校准。比较［(||D1B1|－|D2B2||)+(||E1B1|－|E2B2||)］和［(||D1C1|－|D2C2||)+(||E1C1|－|E2C2||)］大小，误差大者放弃。通过上述防错措施，可实现基准点的高精度测量。

3.2 程序设计

本研究所设计的程序主要解决以下几个问题:

(1)输入各点坐标值和判别各精密球体测量精度;

(2)计算各需要坐标变换点的坐标值。

本研究中的软件设计思路是基于VB(Visual Bas-ic)编程，实现三坐标测量机辅助设备坐标点的计算和精确度判别，程序界面如图5所示。

图5 三坐标测量机辅助设备测试计算软件

4 试验验证及误差分析

4.1 试验及结果

无论是长工件还是短工件，均有:①只要放在所设计制造的平台上，平台移动了450 mm后，被测工件上各点的位置都发生了变化;②变换所用基准点的位置移动量是一致的。

鉴于上述两方面的考虑，为了能简单方便地对所设计平台的性能进行考核，验证试验采用如下方法:

几何量选择:位置公差验证选择两个位置关系:角度和平面度。其中角度利用直角尺，测量直角值;平面度采用1 000 mm平尺。长度(形状公差)考核采用两个球心距。辅助设备试验实物图如图6所示。

基准确定:当工作台移动到一边时(称为A状态)，以直角尺的端面作为工件原点建立工件坐标。利用编程自动测量的方法对6个标准球进行测量，可得到各标准球的球心坐标。笔者通过软件计算并确定最佳基准球，通过基准球坐标点变换来验证基准球的准确性。

图6 辅助设备试验实物图

测试方法:当工作台在A状态时，执行以下步骤:①测量直角尺形成直角的两个面(a面和b面)，并构造角度(直角1);②测量能够测量到的平尺平面，构造平面度(平面度1);③构造球E和A、B、C的距离。

当工作台移动(移动距离450 mm)到另一边(称为B状态)时，继续测量6个球的球心坐标，与此同时:①重复测量直角尺的两面，构造角度(直角2);②测量平尺在该状态下能够测量的平面，构造平面度(平面度2);③构造球E和A、B、C的距离。

坐标变换:将B状态下获得的球A、B、C、E的球心坐标通过坐标变换至A状态所在坐标，获得球A、B、C、E的球心坐标(此状态称为C状态)，构造球E和A、B、C 的距离。

将B状态下获得的直角尺b面数据进行坐标变换，获得C状态下的b面数据，构造A状态下的a面和C状态下的b面的角度(角度3)。

将B状态下获得的平尺平面各点坐标变换到A状态下各点坐标，获得C状态下的各点坐标，构造A状态下的各点坐标和C状态下的各点坐标共同形成平面，计算平面度(平面度3)。

数值验证:比较各状态下的角度、平面度、球心距离，具体数据如表1所示。

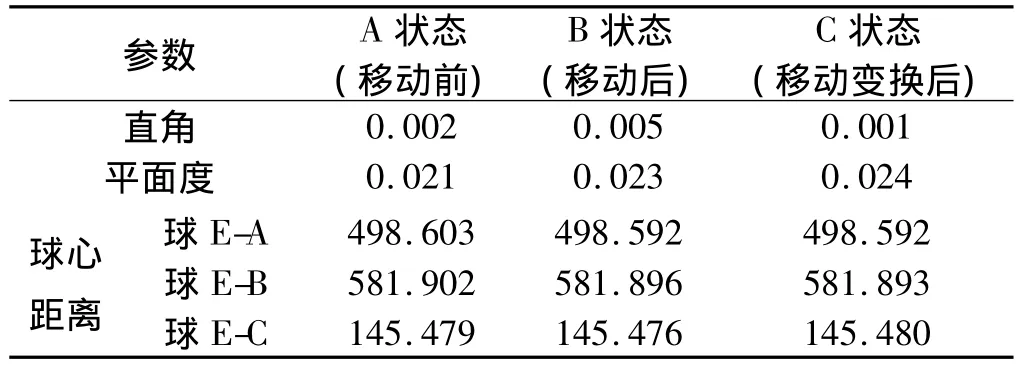
表1 超长零件测量验证结论表(单位:mm)

从所验证的方法和数据可以得出:

(1)直角参数在各种状态下所测值都小于0.005 mm/1 000 mm，最大误差为0.004 mm/1 000 mm。

(2)平面度参数的最大误差是0.003 mm/1 000 mm。

(3)球心距离最大误差是0.011 mm，三坐标本身两次测量的平均误差是0.07 mm，所以辅助机构的误差小于0.011 mm，按误差简单线性累加的原理计算可以得到辅助机构的误差为0.004 mm。

(4)测量位置公差(角度、平面度)所获得的数据比测量形状公差(距离)所获得的数据精度高。这是因为测量形状公差(尤其是长度、距离)时，所有误差都是累加的。而测量位置公差(如角度)时，其误差能进行部分抵消，甚至在构造几何形状中能把部分劣质数据剔除。故该系统更适合于大尺寸的位置公差的测量。

4.2 误差分析

在精密测量中，一般提高测量精度方法有:①提高设备结构精度;②减小环境因素带来的影响;③采用适当的采样策略［10］。本研究也从这几个方面去分析测量误差，通过试验分析可知，主要影响超长零件测量精度的因素有:①测量机和辅助设备的精密性;②基准球的表面质量和球度;③基准球测量精度和精度级别判断准确性;④测量环境和测量点的选择。为了减少测量误差，需要对上述4个方面进行重点关注，提高设备精度、使用高精密基准球、优化数据判别能力。

5 结束语

本研究基于理论分析和实际三坐标测量机机构，制造了一套基于三坐标测量机的超长零件形位公差测量装置，同时在超长零件测量上，利用移动平台中精密几何体的特征，设计了相应的测量软件。笔者分析了测量过程中精度的影响因素，优化了设计方案和测量方法，实现了超长零件形位公差的精密测量，达到了在测量长度上由原来的750 mm扩展到了1 200 mm的要求。数据计算、判断和相关修正通过VB编程实现，提高了测量效率和准确性。研究结果表明，超长零件的测量数据精度符合测量要求，实现了超长零件形位公差的精密测量。

［1］单 岩，魏志刚，梁建国.反向工程中三坐标测量重定位整合［J］.模具工业，2001(8):8-11.

［2］刘之江.反求工程［M］.北京:机械工业出版社，1996.

［3］李 剑，王恒奎.三维曲面非接触式测量系统机械设计及误差补偿研究［J］.机电工程，2001，18(1):48-51.

［4］XING Yuan，XING Zhen-rong，WANG Hai-bin.Research on integrated reverse engineering technology for forming sheet metal with a freeform surfaee［J］.Journal of Materials Proeessing Teehnology，2001，112(2-3):153-156.

［5］YIN Zhong-wei.Reverse engineering of a NURBS surface from digitized points subject to boundary conditions［J］.Computers ＆ Graphies，2004，28(2):207-212.

［6］李建军，温建勇，肖祥芷.逆向工程及其相关技术［J］.机械与电子，1999(3):16-18.

［7］许志龙.逆向工程中多视角点云数据拼合技术［J］.组合机床与自动化加工技术，2006，13(1):26-28.

［8］丁 燕，蔡一湘，张立华.粉末冶金制品三坐标测量的基准定位方法［J］.广东有色金属学报，2003，13(1):68-72.

［9］吴立军，何培峰，王瑞金，等.基于几何体中心的三坐标测量数据重定位整合技术［J］.新技术新工艺，2007(5):65-67.

［10］CASKEY G，HAIR Y，HOCKEN R，et al.Sampling Techniques for Coordinate Measuring Machines［C］//Proceedings of the 1991 NSF Design and Manufacturing Systems Conference，Austin.Texas，USA:［s.n.］，1991:779-786.