基于混沌理论的微弱信号检测及自跟踪扫频电路实现*

吴 敏，赵文礼，周 芳

(杭州电子科技大学机械工程学院，浙江杭州 310018)

0 引 言

从强噪声背景中检测微弱的有用信号是工程应用中的重要内容，前人已经开展了大量的研究工作。传统的基于线性理论的信号检测方法由于对噪声背景下的输出信噪比难以提高而存在局限性，尤其对强噪声背景下的微弱信号检测更是受到限制。然而很多研究证明，利用“混沌振子对周期小信号具有敏感依赖性，而对噪声具有免疫性”的特点［1-2］，从强噪声背景中提取微弱的周期信号是一种行之有效的方法，引起了人们极大的兴趣。1995年Haykin［3］利用人工神经网络方法实现了混沌背景噪声中的小信号提取。

1996年Leung［4］利用MPSV方法进行了混沌通信系统中如何提取有用信号的研究。之后Wang Guan-Yu等人［5-6］利用混沌测量系统实现了白噪声背景下信噪比低达－66 dB的正弦信号的测量，成功提取了谐波信号;2004年李月、杨宝俊［7］提出了在色噪声背景下nV级正弦信号、方波信号、周期脉冲信号的混沌测量方法。文献［8］作了基于Duffing振子系统的电路仿真试验研究;文献［9］中开展了微弱信号检测的试验电路研究，并对2 Hz、20 Hz和60 Hz频率下的微弱信号进行了检测试验;文献［10］研究了如何利用混沌控制实现对微弱信号的检测。目前关于微弱信号检测虽然有了理论计算以及实验验证，但是实际的效果却缺乏说明。

本研究针对工程实际中常见的中、低频率信号开展微弱信号的自跟踪扫频检测方法的研究，并设计制作相应的自跟踪扫频检测电路，从而实现在噪声背景下的中、低频率微弱周期信号的检测。

1 混沌系统检测微弱信号基本原理

通过对Duffing振子混沌过程的控制实现微弱信号的检测是经典的方法之一，即利用混沌系统对参数及初值具有敏感依赖性的特点，通过控制混沌系统从临界状态到周期态形态的变化进行微弱周期信号的检测，Duffing方程的具体形式为:

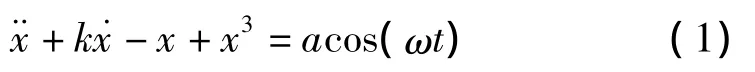
式中:k—阻尼比;－x+x3—非线性恢复力;acos(ωt)—周期策动力;a，ω—周期策动力的幅值、频率。

这是一个描述非线性动力学的运动方程。

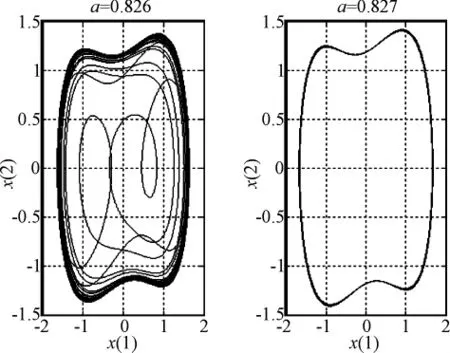
图1 大尺度周期轨迹

在调整周期策动力的强度从小到大时，系统相平面(x，x˙)将会出现有规律的变化:历经同宿轨迹、分岔轨迹、混沌轨迹、混沌临界轨迹、大尺度周期轨迹。假设ω=1，并取阻尼比k=0.5，仿真发现混沌临界轨迹经过很小的激励变化(a由0.826增大到0.827)即会进入T=2π的大尺度周期轨迹，如图1所示。

2 适应不同检测频率的控制方法

Duffing振子检测微弱信号方法实质上就是如何实现对混沌的有效控制［11］。为了使系统能检测任意频率的信号，本研究对式(1)所示系统改进为如下方程:

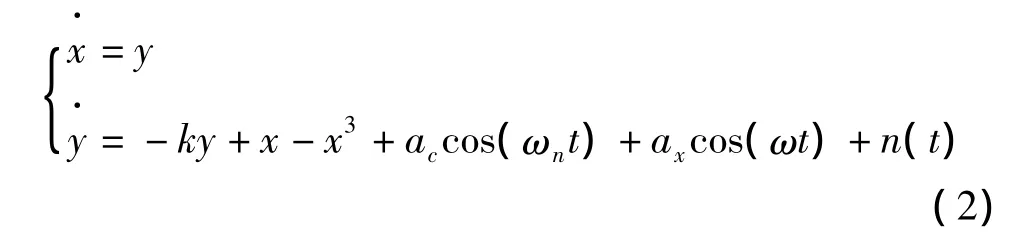
式中:accos(ωnt)—驱动系统的扫频控制信号，axcos(ωt)+n(t)—待测信号，n(t)—高斯白噪声。

对于不同的控制信号accos(ωnt)，利用Melnikov方法可以求出Duffing振子存在混沌的阈值为［12-14］:

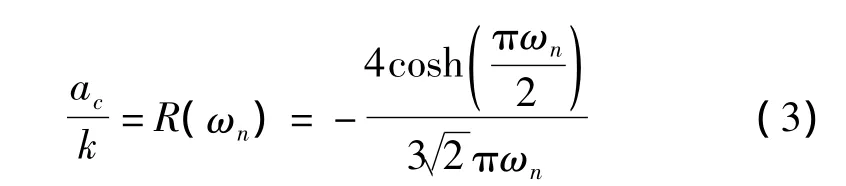
由此可知，不同的频率对应不同的混沌阈值。为了进行微弱信号的检测，必须求得不同频率时混沌阈值所对应的控制信号幅值。如ω1对应于ac1=kR(ω1)，ω2对应于 ac2=kR(ω2)，ωn对应于 acn=kR(ωn)等。

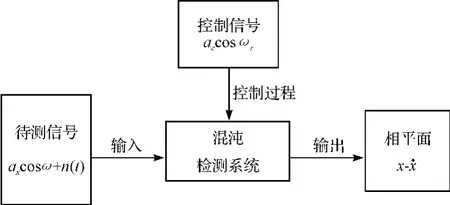
图2 检测原理图

混沌振子检测原理如图2所示，其中策动力(即扫频控制信号)为accos(ωnt)，待测信号为axcos(ωt)+n(t)，首先将扫频控制信号输入到混沌系统中，调整扫频控制信号强度至混沌阈值，此时相平面为混沌临界状态，输入待测信号，若待测信号与驱动力频率相同，输出相图转变为大周期状态，若使用相关滤波方法，当信号同频时，相关性最大，但是当微弱信号绝对强度低到nV级别或者噪声强度超过信号强度10倍以上时，相关滤波方法并不理想。

根据检测原理图，取阻尼比k=0.5，令x=v1，y=v2，则方程式(2)对应的电路状态方程为:

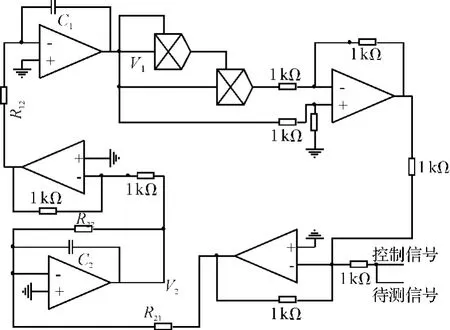
图3 检测电路图

选定电阻R22=2R21=2R12，其中积分电容C1=C2=C，通过改变电阻阻值和积分电容的大小可以使电路适应不同频率的正弦信号。根据式(4)设计的原理图如图3所示。根据图3所示，本研究选定电阻为R22=2 kΩ，R12=R21=1 kΩ，只需要通过调整电容 C1、C2以适应不同频率的信号检测。

3 自跟踪扫频控制方法及其电路实现

在工程实际中，待测信号的频率往往是未知的，或者只知道某一个大致的范围。为了实现未知微弱信号的自跟踪检测，该设计采用芯片合成控制信号作为扫频信号输入Duffing振子检测电路中，利用单片机使控制信号扫频输出，在控制信号扫频的过程中，通过单片机实时调整Duffing振子检测电路的电容C1、C2，以适应不同频率的信号检测，识别淹没在强噪声背景下的微弱信号，具体实现介绍如下。

3.1 控制信号的合成

该设计采用Atmega16A控制AD9850芯片产生扫频信号，然后经过幅值调整模块将控制信号的强度调整为混沌临界状态阈值。

AD9850芯片是一种高性能DDS芯片，主要由可编程DDS系统、高性能模数变换器(DAC)和高速比较器3部分构成。AD9850芯片在有一个精确的时钟源作为参考频率源时，能产生一个频谱很纯的频率或相位可编程的模拟正弦波输出，AD9850包含一个40位控制字，32位用于频率控制，5位用于相位控制，1位用于电源休眠控制，2位用于选择工作方式，可以通过并行或者串行方式送入器件，在串行传输模式下，通过总线D7向AD9850芯片输入频率控制字，设定初始相位为零，则只需要输入32位频率控制字，其他位默认为零，AD9850的工作原理如图4所示。

AD9850的输出正弦波的频率计算公式为:

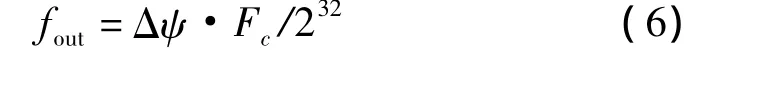
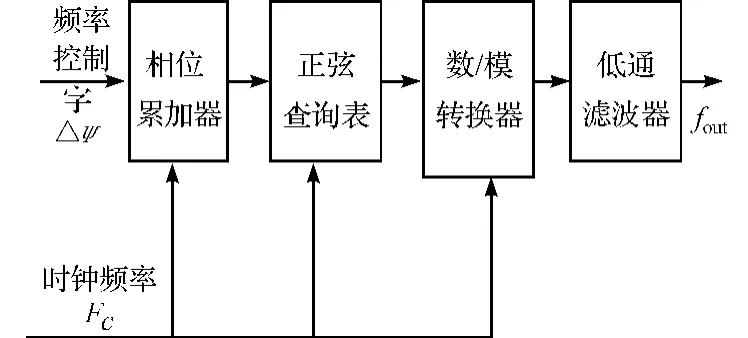
图4 AD9850原理框图

式中:Δψ—32位频率控制字的值，fout—输出信号频率，Fc—参考时钟频率。

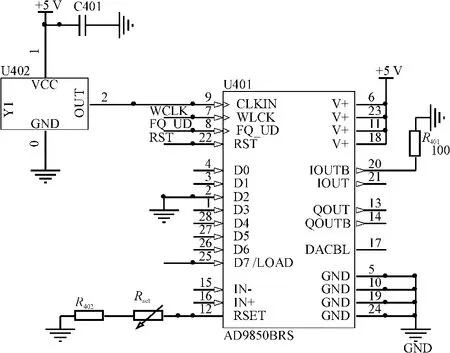
图5 AD9850电路图

如图4所示，AD9850采用32位的相位累加器将信号截断成14位输入到正弦查询表，查询表的输出在被截断成10位后输入到DAC，DAC输出两个互补的电流。DAC满量程输出电流通过一个外接电阻RSET调节，调节关系为ISET=32(1.248/RSET)，当这个外接电阻大小确定，输出正弦波幅值随之确定，该设计通过调节RSET，使输出控制信号峰峰值为1 V，AD9850输出信号为cos(2πfoutt)。电路原理如图5所示，其中，D2引脚接地表示串行通信，第7、8、22引脚为控制信号输入，第25引脚为频率控制字输入口，第21引脚为输出信号。

AD9850输出频率分别为10 Hz、1 000 Hz的正弦信号如图6所示。

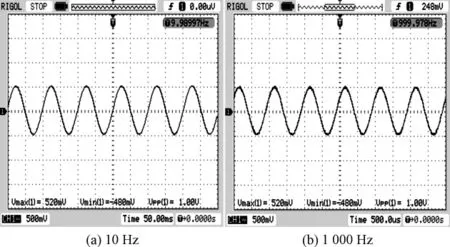
图6 AD9850芯片生成的控制信号

为了获得能够使混沌检测电路处于混沌临界状态的控制信号，需要进一步调整由AD9850芯片输出的控制信号，使它的强度处于混沌阈值。该设计采用可编程数模转换器TLC5615、乘法器AD633或乘法器AD534、运放电路实现控制信号幅值的调整，其中每个频率对应的混沌阈值存储在Atmega16A单片机的存储器ROM中，控制信号频率改变时，单片机读出需要的阈值输入到幅值调整模块。

TLC5615是串行10位D/A转换器，最大输出电压是基准电压值的2倍，具有上电复位功能，只需要3条串行总线就可完成10位数据的串行输入，TL5615的输出函数为:

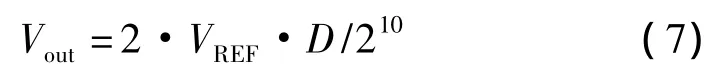
式中:VREF—参考电压，可选2.5 V 或者3.0 V，该设计选2.5 V;D—控制字，根据需要软件可编程设置。

微处理器控制TL5615，实现10位幅值调节，精度达0.005 V。本研究将TLC5615输出的直流电压与AD9850输出的正弦信号输入到乘法器后，经过运放线性放大(放大3倍)便可得到符合要求的扫频控制信号，幅值调整原理如图7所示。

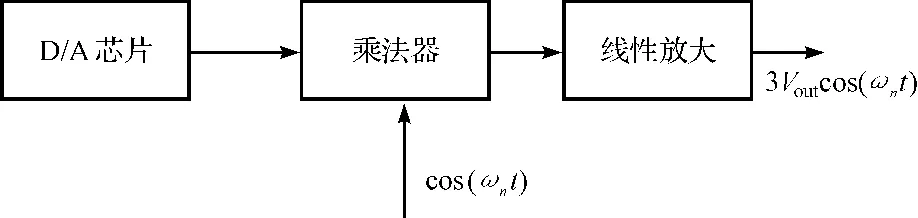
图7 幅值调整原理图

由于TL5615的输出精度为0.005 V，如图7所示，经过线性放大后输出控制信号精度达到0.015 V，通过调整控制字D，可以得到强度在0～15 V区间的控制信号。幅值调整模块电路原理图如图8所示。通过微控制器调整输入幅值调整模块的控制字D=512，得到10 Hz、1 000 Hz的输出控制信号实例如图9所示。

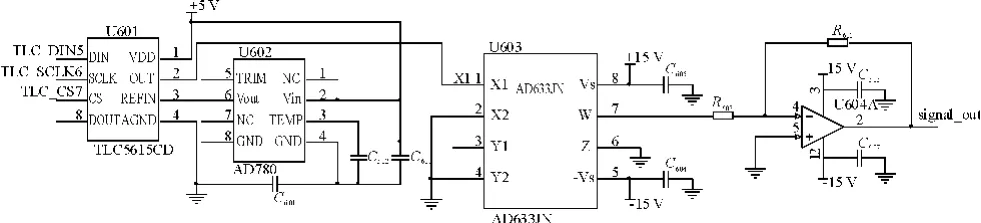
图8 幅值调整模块原理图

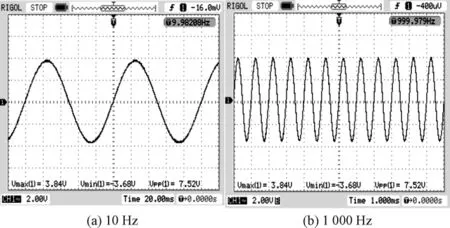
图9 幅值调整后控制信号

3.2 自跟踪扫频的实现

该设计采用Atmega16A单片机作为控制单元，控制检测电路所需控制信号的生成;在控制信号扫描过程中，如图3所示电路中，电容C1、C2根据控制信号的频率实时改变，该设计采用继电器控制检测电路电容的调整，继电器控制部分如图10所示，通过单片机引脚控制继电器的开关K通断来改变检测电路电容参数，以适应不同控制信号频率。

系统原理框图如图11所示:系统上电初始化后，通过输入模块设定初始值，包括扫频间隔时间t(间隔时间t需确保检测电路的输出相图稳定)、根据估计输入(实际工程中一些故障能够知道信号的大概频率范围)控制信号扫频范围ω1～ω2、扫频步长b(根据需要进行粗扫、细扫);按“扫频”键后，系统控制信号从频率 ω1开始扫频，经过时间 t，2t，3t，…，nt，…后，控制信号频率为 ω1+b，ω1+2b，ω1+3b，…，ω1+nb，…，直到控制信号频率为ω2，系统停止扫频;扫频期间若相图没有出现大周期状态，则待测信号频率不在ω1～ω2之间，需要重新评估待测信号频率范围，重新扫频;若扫频过程中检测模块输出相图能稳定在大周期状态，此时按“暂停”键，系统停止扫频，显示模块显示控制信号频率为ω、强度为a1;然后按下“幅值扫描”键，控制模块控制幅值调整模块将控制信号的强度逐渐减小，等待检测模块输出相图重新回到混沌临界状态，按下停止键，控制信号强度不再减小，此时显示模块显示控制信号强度改变为a2。因此待测信号即为频率ω，强度为a1－a2。软件流程图如图12所示。

图10 继电器控制部分

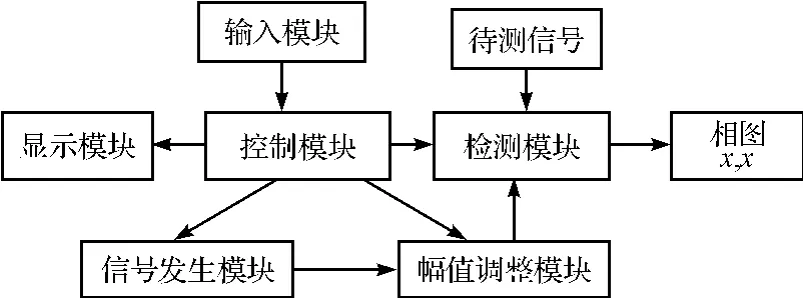
图11 系统原理款图

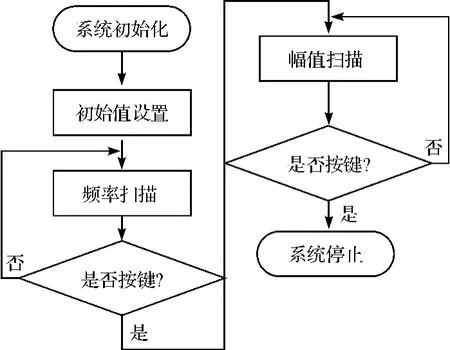
图12 软件流程图

4 噪声背景下微弱信号的扫频检测

假设一个微弱信号频率为100 Hz，峰峰值为0.1 V，本研究将其作为待测信号加入到如图3所示检测电路中，设置好系统初始值，设置扫频范围为95 Hz～105 Hz，扫频间隔时间为10 s，扫频步长为1 Hz，然后按“扫频”键，系统开始扫频，在检测电路输出相图如图13(b)所示大周期状态;按下“暂停”键，系统停止扫频，显示模块显示控制信号频率为100 Hz，峰峰值为2.7 V;然后按下“幅值扫描”键，控制信号强度开始减小，检测模块再次进入如图13(a)所示的混沌临界状态后，按下停止键，显示模块显示频率为100 Hz，峰峰值为2.6 V，故待测信号的频率为100 Hz，峰峰值为0.1 V。

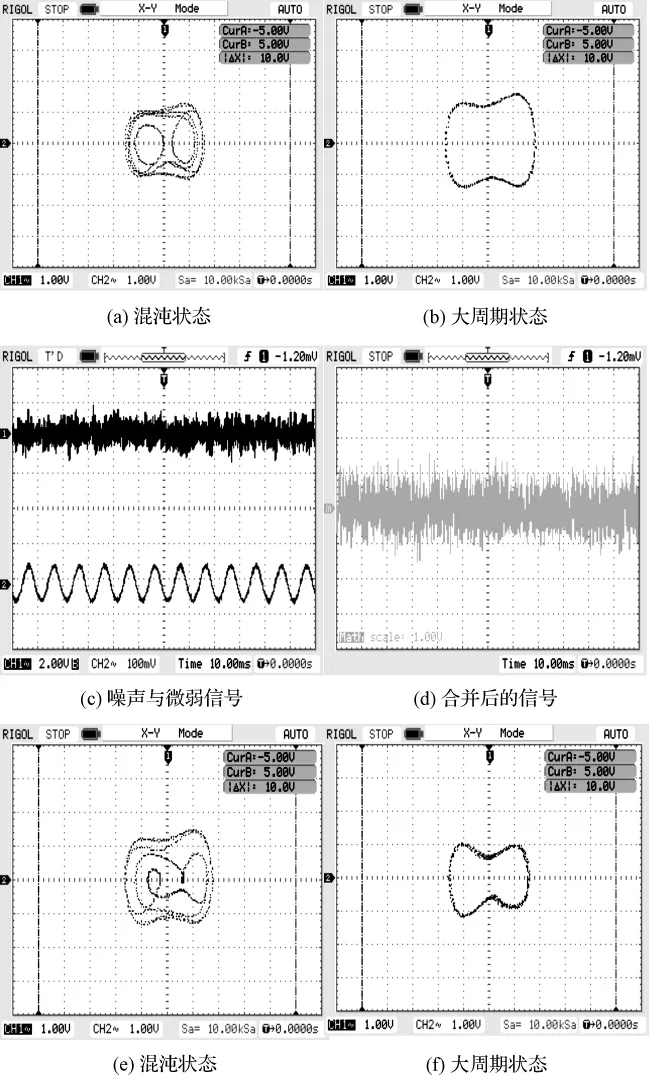
图13 示波器显示图

如图13(c)所示的正弦信号频率为100 Hz，峰峰值为0.1 V，高斯白噪声强度为10 V;两个信号经加法器合并后如图13(d)所示，此时SNR=－40 dB;将如图13(d)所示的信号加入混沌电路后，扫频输出相图混沌临界状态和大周期状态分别如图13(e)、13(f)所示。

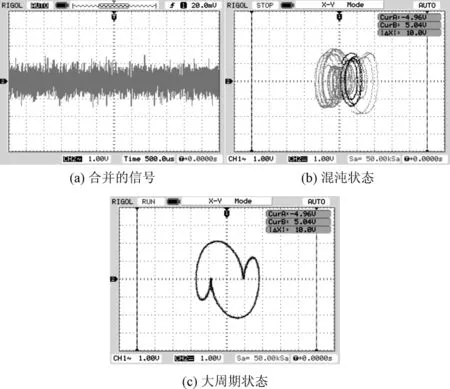
图14 示波器显示相图

示波器显示相图如图14所示，合并的信号如图14(a)所示，并不能看出该信号中是否含有周期信号，本研究将图14(a)所示信号作为待测信号送入检测电路，按照第3.2节中所述检测步骤，设定扫频范围为100 Hz～400 Hz;频率扫描步长为1 Hz，然后开始频率扫描，当控制信号为293 Hz时，示波器显示为如图14(c)所示的大周期状态，此时LCD显示控制信号峰峰值为7.3 V，然后按键控制开始控制信号幅值扫描，控制信号强度开始减小，当控制信号的峰峰值显示为7.2 V时，示波器相图显示为如图14(b)所示混沌状态，可知待测信号中含有293 Hz的正弦信号，且峰峰值为0.1 V。因此，淹没在强噪声背景下的微弱信号能够被有效地识别出来。

5 结束语

该设计根据Duffing振子原理实现了微弱信号的检测电路，在检测电路的基础上进行微弱信号自跟踪扫频方法的研究，使电路具有了一定的自适应性，最后完成了微弱信号的自跟踪扫频检测电路，利用AD9850、TLC5615等数字芯片产生扫频信号，利用继电器进行参数的自动跟踪控制，通过AVR芯片控制继电器的通断来实时的控制混沌检测系统内的电容参数，使系统扫频过程中处于临界状态，等待微弱小信号的合并，进入大尺度周期状态，确定小信号的信息;最后实验结果表明，该电路实现了噪声背景下一定范围中低频率微弱正弦信号的检测。

［1］谌 龙，王德石.基于Lorenz系统的微弱谐和信号检测［J］.仪器仪表学报，2007，28(11):2034-2038

［2］冯 奇.噪声对杜芬振子的混沌性质的影响［J］.同济大学学报，1994，22(1):69-75.

［3］HAYKIN S.Neural Nerworks，Acomprehensive Foundation［M］.Prentice Hall，Englewood Cliffs，NJ，1999.

［4］PILGRIM C J，LEUNG Y K.Appropriate use of the Internet in computer science courses［C］//Proceedings of the 1st conference on Integrating technology into computer science education.Barcelona，Spain:［s.n.］，1996:81-86.

［5］WNAG Guan-yu，CHEN Da-jun，LIN Jian-ya，et al.The application of chaotic oscillators to weak signal detection［J］.IEEE Transactions on Industrial Electronics，1999，46(20):440-443.

［6］WANG Guan-yu，WEI Zheng，HE Sai-ling.Estimation of amplitude and phase of a weak signal by using the property of sensitive dependence on initial conditions of a nonlinear oscillator［J］.Signal Processing，2002，82(1):103-115.

［7］李 月，杨宝俊，石要武.用特定的混沌系统检测弱周期脉冲信号［J］.仪器仪表学报.2002(S1):35-36.

［8］王永才，肖子才.Duffing混沌系统电路仿真研究［J］.电路与系统学报，2008，13(1):132-135.

［9］赵文礼，黄振强，赵景晓.基于Duffing振子的微弱信号检测方法及其电路实现［J］.电路与系统学报2011，16(6):120-123.

［10］朱少平，钱富才，刘 丁.基于两级算法的混沌控制［J］.控制理论与应用，2010，27(9):1259-1.

［11］王冠宇.混沌振子在具有强噪声背景的信号检测中的应用［J］.仪器仪表学报，1997，18(2):209.

［12］夏其表，王 洁.基于虚拟仪器的精密球研磨加工的振动信号检测［J］.轻工机械，2011，29(2):79-82.

［13］李 月，杨宝俊.混沌振子检测引论［M］.北京:电子工业出版社，2004.

［14］BARTK S.Adaptive Stochastic Resonance［C］//Proceedings of the IEEE 1998.San Franeisco:［s.n.］，1998:2182-2183.