热冲击下的复合材料壳刚柔耦合动力学研究

潘科琪，刘锦阳

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

在热冲击载荷作用下，复合材料的各向异性性质将引起大范围运动和拉伸变形、弯曲变形、扭转变形、剪切变形和翘曲变形的相互耦合，呈现高度非线性特征。在轨航天器的太阳翼展开，或者航天器变轨的过程中，受到太阳辐射的影响，其热流条件的突变，其温度场会发生变化，从而容易诱发天线的热振动，影响航天器的姿态运动。复合材料在航天器中的广泛应用，弹性变形对航天器姿态运动的影响愈加明显，因此对复合材料薄壁柔性附件精确的变形位移描述是提高复杂结构航天器仿真精度的前提，也是航天器安全性的保障。为了保证刚－柔耦合动力学仿真精度和动应力的计算精度，建立复合材料层合壳多体系统的动力学模型是很有必要的。

前人工作表明，复合材料层合壳的横向剪切变形影响比各向同性材料显著。对于高模量复合材料(例如碳硼纤维增强机体复合材料)，在厚跨比h/L小于1/30时，横向剪切变形的影响不可忽略。基于Mindlin假设，假定垂直于中面的法线在变形后仍为直线，以3个中面变形位移u，v，w和2个法线转角φx，φy为变形位移坐标，非中面上任意一点的变形位移的表达式中包含u，v，w，φx，φy与z的一次项，建立复合材料层合板的动力学模型。基于复合材料板理论，Ding等［1］研究了闭合复合材料壳的热弹性耦合特性。Krejaa等［2］在应变－位移关系中考虑高次项，研究了大变形复合材料层合壳的动力学特性，Abea等［3］研究了一边固支的复合材料层合壳的共振特性，Zhou等［4］基于几何非线性理论对复合材料层合壳的运动稳定性进行了分析。

随着复合材料在工程中的大量应用，近几年来，国内外学者对复合材料多体系统的动力学开展了一系列工作。Yoo等［5］等考虑几何非线性和横向剪切变形，研究了作旋转运动复合材料梁的频率特性。刘锦阳等［6］建立了复合材料梁系统的动力学模型，研究了温度变形对复合材料梁动力学特性的影响。Neto等［7］基于线弹性理论，建立了复合材料层合板多体系统的动力学模型，在建模过程中考虑了横向剪切变形，但是没有考虑几何非线性。Yoo等［8］研究了作旋转运动复合材料层合板的频率特性，考虑几何非线性的影响。同样，在热载荷下的复合材料曲梁也是力学界研究的重点，早在1992年，Huang等［9］研究了受瞬时热冲击的壳的动力学特性，Khdeir等［10］使用模态方法研究复合材料壳的瞬时受热问题。Oguamanam等［11］关于复合材料圆柱壳在温度场的大范围运动的动力学性能的分析采用16节点的等参拉格朗日差值的单元，研究对象为常曲率的壳结构，使其在工程中的适应性受到很大的限制。

基于Mindlin假设，考虑了几何非线性和材料的各向异性，建立了任意形状复合材料壳的刚柔耦合动力学模型，研究了在热冲击的条件下，中心刚体－复合材料壳动力学响应。为了提高计算的精度，采用了16节点的等参单元进行差值，由于节点数目较多，广义质量阵、力阵较为复杂，采用高斯积分法对常值阵进行积分。壳的动力学方程为高度非线性的微分代数方程，为提高计算效率，将广义－α法结合Newton-Raphson迭代法对刚－柔耦合的动力学方程进行积分，求出了动力学响应的时间历程。最后给出了仿真算例，对复合材料壳的动力学特性进行了研究。

1 复合材料壳的数学模型

图1表示一个中心刚体和一个任意形状柱状壳结构，壳的一端固支与中心刚体。为了方便描述，引入了惯性坐标系，连体基坐标系0(bbb)以及局部坐标系c。图2表示壳的中线面在连体基坐标系bb面的形状，z=f(x)为形函数，对于只有一个方向曲率的柱状壳，柱状壳在连体基上的方程为以及连体基内任意点的曲率半径么分别为:

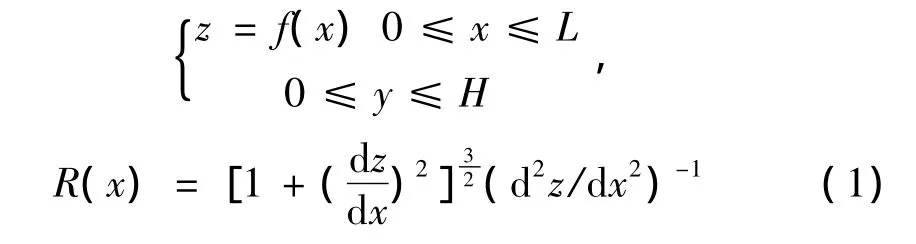
其中:H表示壳宽度方向的长度。

设热冲击ΔT沿壳的厚度方向均匀分布，具体表示为:

图1 复合材料层合壳Fig.1 Laminated composite shell

其中:ΔTss为温度载荷稳态时的幅值，t为仿真时间，Tf与热冲击时间相关的温度常数。

图2 任意形状壳在连体基面的投影函数bbFig.2 The functions of shell center plane in body coordinate with arbitrary shape

根据Mindlin理论，壳上非中面上任意点的变形可以表示为:

2 复合材料壳的运动学描述

式(6)的变分表达式以及相对于时间的二阶导数分别为:

其中:

3 有限元离散

等参单元离散，上任意点变形和转角可以分别表示为:

其中:－1≤ξ，η≤1，ξ，η均为无量纲变量，pe为单元坐标阵为 Ni，i=1，2，3，4，5 为型函数，具体表达式请参见附件。

单元上任意点的在连体基上的坐标可以差值为:

根据式(11)，壳体微元表示为:

其中:h为壳的厚度，ls为曲线的弧长。Jxe=

根据式(3)～式(5)以及式(10)，任意点在e→c上的变形为:

4 考虑热效应的应力应变关系

结合式(9)和(10)，考虑几何非线性的壳结构的应变－位移关系［11］可以表示为:

考虑热载荷及横向剪切变形的复合材料板第k层应力应变的本构关系为:

其中:

5 动力学方程

采用虚功原理来建立系统的动力学方程，对于任意单个壳体，不计体力以及其它外载荷情况，虚功原理的形式如下:其中:δWf为惯性力的虚功，δWin为弹性力的虚功:

设中心刚体－复合材料壳系统的广义坐标q=［θpT］T，根据式(10)和式(11)，并结合有限元离散化方法，惯性力的虚功表示为:

其中:

各项具体表示为:

其中，常值阵为:

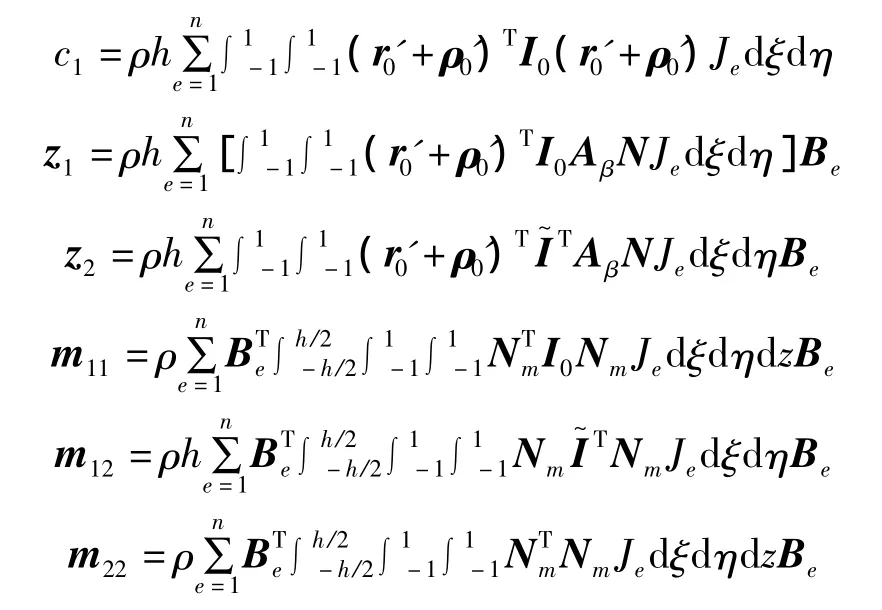
将式(25)和式(26)代入上式，得到复合材料壳弹性力的虚功为:

其中:N为复合材料的层数。

需要特殊说明的是因为δCΘ=CδΘ，所以非线性应变的变分可以表示为:δεN=CGδpe，据式(33)，复合材料壳的弹性力的虚功可以具体表示为:

其中:fb，fs，fT具体表达式为:

其中:矩阵 A，B，D，Aα，Bα的表达式请参见文献［12］。

几何非线性变形与热载荷耦合引起的弹性力表示为:

若铰约束方程为Φ(q，t)=0，系统封闭的第一类拉格朗日动力学方程为:

其中:λ为拉格朗日乘子坐标阵。

6 数值计算方法

本文将广义－α［13］法和Newton-Raphson迭代法结合求解动力方程(24)，为了方便表述，将动力学方程表示为:

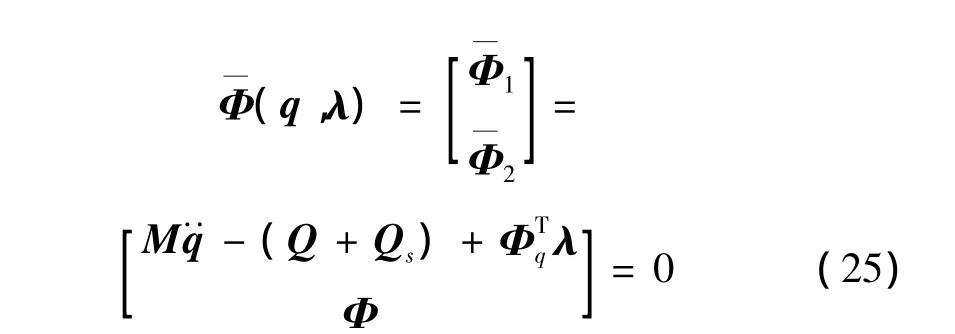
主要步骤为:

(1)基于前一时刻t的动力学响应，根据广义－α法的预估关系式估计下一时刻t+Δt的位移、速度、加速度第一次(n=1)的迭代值为:

(3)根据式(27)，第 n+1次的迭代值可以表示为:

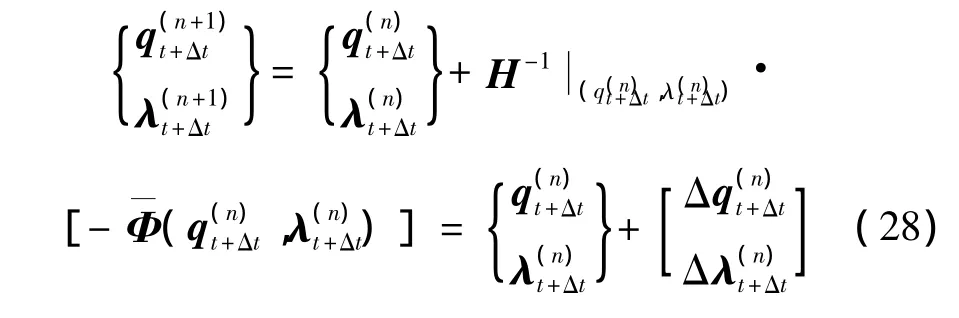
(4)第n+1次的速度、加速度以及拉格朗日乘子的迭代值可以表示为:

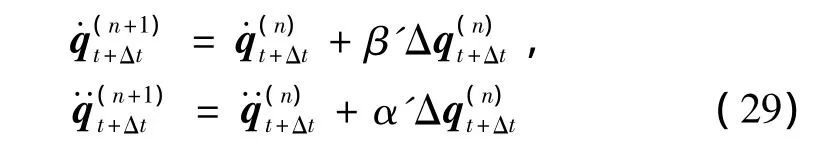
其中:α'=(1 －αm)/［Δt2α(1 －αf)］，β'=β/(Δtα)

(5)将位移、速度、加速度代入式(25)中的Φ—1，判断是否满足允许误差:

若在某次的迭代值满足上式关系，则把其作为t+Δt时刻动力学响应精确值，返回第一步进行下一时刻的动力学响应的求解。

7 仿真算例

其中，本算例中 H=0.1 m，L=0.8 m，d分别取为0.05 m，0.10 m，0.15 m 以及 d=0。d=0 时壳变为平面板。由图3可知，若L保持不变，d越大曲率越大，本算例中H和L都保持不变。

图3 仿真算例复合材料壳在连体基坐标bb面的函数Fig.3 The projection functions in simulating example

复合材料的材料参数为:弹性模量E1=181 GPa，E2=103 GPa，G12=G13=7.7 GPa，G23=2.87 GPa，复合材料的铺层为对称形式［0°/90°/0°/90°/0°/0°/90°/0°/90°/0°］，泊松比 v12=0.28，主方向的热膨胀系数分别为 α11=2.08 × 10－8，α22=22.5 × 10－6，密度 ρ=1 560 kg/m3。本算例中热冲击时间即式(3)中的Tf=0.2 s，热冲击在稳态值即式(3)中的ΔTss=2 K。中心刚体的转动惯量J0=0.01 kg·m2。初始时刻中心刚体－壳系统的角速度均为零。热冲击作用下引起壳结构变形，并且由于刚－柔耦合的作用，壳结构变形的同时也引起了中心刚体的转动。

7.1 本文模型正确性和收敛性的验证

为了验证本文模型的正确性，在中心刚体被约束不动的情况下，将本文提出的等参单元计算的悬臂壳的频率与ANSYS软件用壳单元离散得到的频率进行对比，对比结果如表1所示。从表中可以看出，无论曲率较大d=0.15m还是较小d=0.05m时，通过本文模型计算得到的结果与ANSYS软件计算得到的结果误差都在5%，说明现有模型的正确性。

为了验证本文单元的收敛性，在中心刚体不受约束、初速度为零、有热冲击的情况下，对曲率较大，d=0.15 m的情况下进行了动力学仿真，如图4所示为非线性模型计算得到的中心刚体的转角，可以看到最多15个单元就可以收敛证明了本文单元的收敛性。

表1 现有方法与ANSYS软件的频率比较Tab.1 Comparison of present frequency results with those obtained by ANSYS Software

7.2 线性和非线性模型动力学响应比较

如图5～7中所示为 d=0.15 m，d=0.05 m，d=0 m的工况下，线性模型和非线性模型在热冲击作用下的纵向变形对比图。图5所示为d=0.15 m时，线性模型和非线性模型纵向变形的对比。由图5可见线性模型在热冲击载荷作用下，纵向变形明显小于非线性模型，热冲击稳态时纵向变形有高频振荡，而非线性模型的时间历程曲线较为平滑。线性模型与非线性模型的仿真结果差异显著，主要是由于线性模型没有考虑几何非线应变项εN，热冲击作用下的仿真结果误差较大。如图6和图7所示分别为d=0.05 m和d=0 m时纵向变形的对比，可以看到当d=0.05 m时，线性和非线性模型的结果差异比d=0.15 m时二者的差异有显著地减少。当d=0 m时，即没有曲率时，线性和非线性模型的结果几乎没有差别，说明壳结构比平面板结构在受到热冲击时更容易产生非线性效应，并且曲率越大非线性效应越明显。

图4 非线性模型仿真结果Fig.4 Results of nonlinear model

图5 纵向变形Fig.5 Longitudinal deformation

图6 纵向变形Fig.6 Longitudinal deformation

7.3 曲率、材料属性对动力学响应的影响

本小节的结果均为非线性模型计算得到。图8和图9为不同曲率的复合材料壳在热冲击下的动力学响应。从图8可以看出，曲率越大，也是d越大，纵向变形越明显。同样，从图9可以看，曲率越大，中心的刚体的转角就越大。另外，从图8还可以看出，d=0和d=0.05时的纵向变形差异较小，热载荷稳态时，两者幅值的差异值不到d=0和d=0.1时的差异值的1/3倍，但是如图9所示，d=0和d=0.05时的中心刚体的转动角度差异值已经接近d=0和d=0.1时转角差异值的1/2，说明由于刚柔耦合的作用，微小的纵向变形就能引起较大的中心刚体的转动。

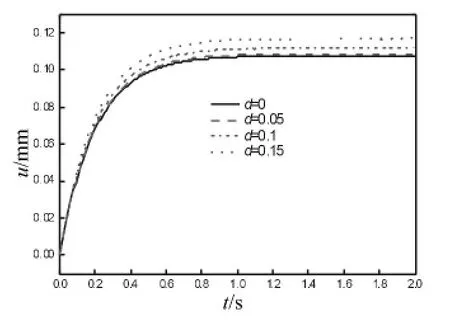
图8 纵向变形Fig.8 Longitudinal deformation

图9 中心刚体的转角Fig.9 Rotation angle of the center hub

图10 中心刚体的转角Fig.10 Rotation angle of the center hub

为了研究热冲击工况下异性材料和同性材料对系统的动力学响应的影响，图10对比了复合材料和同性材料壳的仿真结果。本文定义的同性材料是将算例中的复合材料参数设置为E1=E2=181 GPa，G12=G13=G23=7.7 GPa，并将铺层设为对称形式［0°/0°/0°/0°/0°/0°/0°/0°/0°/0°］，热膨胀系数 α11= α22=22.5 ×10－6，其它参数都变，此时可以视为同性材料，以便减少其它因素的引入对计算结果的影响。同性材料和复合材料壳的曲率参数d=0.05 m。从图10中可以看出，复合材料壳的中心刚体的转角明显大于同性材料的，这是因为复合材料的各向异性，使得热膨胀引起的热应力分布不均，热应力梯度引起了中心刚体的转动，而同性材料壳，即使有曲率的存在，由于各处热膨胀系数相同，各处的热应变相同，不会对中心刚体产生力偶矩。

8 结论

本文建立了考虑热载冲击的中心刚体－变曲率复合材料壳的动力学模型，并与ANSYS软件计算得到的频率对比说明本文模型的正确性。通过将广义－α法与Newton－Raphson迭代法结合的方式对动力学方程进行积分。仿真结果表明，在热冲击载荷下，复合材料壳线性模型仿真结果误差较大，并且随着曲率的增加，线性和非线性模型的结果差异越明显，需要考虑几何非线性项才能满足精度要求。复合材料壳的曲率越大，在热冲击作用下的纵向变形越大，变形和大范围运动的耦合作用就越明显。同性材料的壳在热冲击作用下不会引起中心刚体的大范围运动。

［1］Ding K W.The thermoelastic dynamic response of thick closed laminated shell［J］.Shock and Vibration，2005，12(4):283－291.

［2］Krejaa I，Schmidt R.Large rotations in first-order shear deformation FE analysis of laminated shells［J］.International Journal of Non-linear Mechanics，2006，41(1):101 －123.

［3］Abea A，Kobayashib Y，Yamada G.Nonlinear dynamic behaviors of clamped laminated shallow shells with one-to-one internal resonance［J］.Journal of Sound and Vibration，2007，304(3－5):957－968.

［4］Zhou C T，Wang L D.Nonlinear theory of dynamic stability for laminated composite cylindrical shells［J］.Applied Mathematics and Mechanics，2001，22(1):53 －62.

［5］Yoo H H，Lee S H，Shin S H.Flapwise bending vibration analysis of rotating multi-layered composite beams［J］.Journal of Sound and Vibration，2005，286(4－5):745－761.

［6］刘锦阳，潘科琪.考虑热效应的复合材料多体系统动力学研究［J］.动力学与控制学报，2009，7(1):9－13.LIU Jin-yang， PAN Ke-qi. Dynamic invetigation on composite flexible multi－body system considering thermal effect［J］.Journal of Dynamics and Control，2009，7(1):9－13.

［7］Neto M A，Ambrósio J A C，Leal R P.Composite materials in flexible multibody systems［J］.Computer Methods in Applied Mechanics and Engineering，2006，195(50－51):6860－6873.

［8］Yoo H H，Kim S K，Inman D J.Modal analysis of rotating composite cantilever plates［J］.Journal of Sound and Vibration，2002，258(2):233－246.

［9］Huang N N，Tauchert T R.Thermally induced vibration of doubly curved cross-ply laminated panels［J］.Journal of Sound Vibration，1992，154(3):485－494.

［10］Khdeir A A. Thermallyinduced vibration ofcross-ply laminated shallow shells［J］.Acta Mechanica，2001，151(3－4):135－147.

［11］Oguamanam D C D，Hansen J S，Heppler G.R.Nonlinear transient response of thermally loaded laminated panels［J］.Journal of Applied Mechanics，2004，71:49 －56.

［12］Pan K Q，Liu J Y.Dynamic investigation on composite flexible multi-body system considering thermal effect［J］.Journal of Shanghai Jiaotong University，2010，15(4):414 －422.

［13］Arnold M，Brüls O.Convergence of the generalized － α scheme for constrained mechanical systems［J］.Multibody System Dynamics.2007，18:185 －202.

［14］王勖成.有限单元法［M］.北京:清华大学出版社，2006.

附 录

16 节点的拉格朗日型单元的型函数 Si，i=1，2，…，16，可参见文献［14］，对角阵 Si=diag(Si)16×16，S=［S1S2S3… S16］，式(9)和式(10)中的差值函数为:Ni=S(i，∶)(i=1，2，3，4，5)，S(i，∶)表示矩阵 S 中第 i行的所有列，(ξ，η)=(S1S2… S16)。