拖靶垂向运动传递函数的求解

王成军 李世秋 郑成军

(辽宁兴城92419部队 125106)

拖靶系统是一类特殊的飞行器系统。拖靶系统主要包括拖带飞机、拖缆和无动力的拖靶。其中拖带飞机一般为有人驾驶飞机，拖缆是一根长度约几千米而直径只有几毫米的钢缆，拖靶多为外形类似导弹的无动力飞行器。拖靶系统的工作特点是用有动力的拖带飞机，通过拖缆牵引着拖靶飞行。

拖靶系统的应用基本上为军事应用，即用拖靶来模拟来袭的导弹类飞行器，以为各种反导弹武器系统提供防御和打击的目标。由于在工作结束后，如果拖靶未被击中，则可以通过缠绕拖缆将拖靶收回，所以拖靶可以多次使用，具有很高的性价比。目前，美英等国家生产和应用的拖靶已经具有多种型号并且形成系列。

在拖靶的设计中，最关键的是高度控制系统的设计，而拖靶垂向运动传递函数是高度控制系统设计的理论基础。我国的拖靶设计生产起步较晚，目前很少见关于拖靶系统设计方面的报道。

1 拖靶的受力分析

考虑到拖靶实际供靶飞行中基本上是一个纵向的等速直线运动，且滚转角速度为零，则可以把拖靶置身于惯性坐标系中，按刚体平面运动来分析。拖靶受力图如图1示。

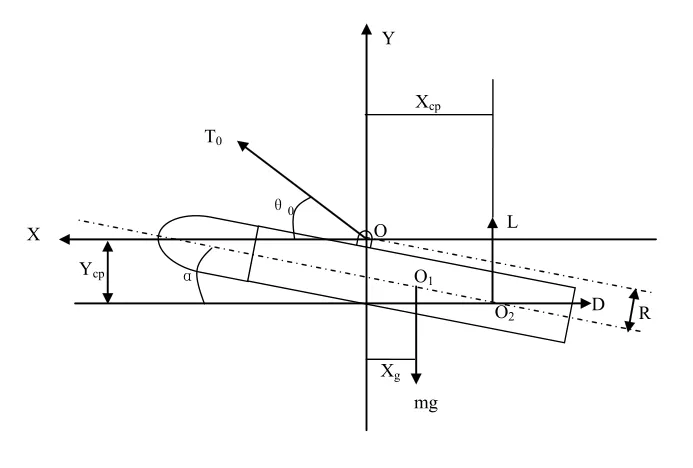
图1 拖靶受力分析图

0－拖靶牵引点，即原点

01－拖靶重心

O2－压力中心

R－牵绕点到轴线距离

Xcp－压力中心到原点水平距离

Ycp－压力中心到原点垂直距离

Xg－重心到原点水平距离

L－升力

D－阻力

T0－牵引点拉力

θ0－拉力相对来流的倾角

mg－拖靶重量

α－拖靶迎角（攻角）

根据受力分析，可以看出，拖靶受力的垂向分量（向上为正）包括重力-mg、牵引点拉力的分量TH和升力L，当拖靶存在垂向的速度时（拖靶的垂向速度远小于水平速度），垂向上还有阻力D的分量Dy。

2 建立拖靶垂向运动的微分方程

根据牛顿第二定律，在垂直方向上可以得到

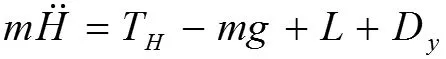
其中H为拖靶的高度。

在这个微分方程中，重力mg是不变的。下面计算其他三个分量。

2.1 计算TH

由于拖缆是长度约为几千米的钢缆，不能作为一个刚体来看待，而且拖靶系统是一个包括飞机、拖缆和拖靶在内的多体运动系统，因此牵引点的拉力计算十分复杂。在此，我们根据小扰动假设，计算在平衡状态附近的张力。首先，可以用静态方法计算出几个平衡点附近不同状态下的拖缆张力值，然后进行线性化处理。方法如下：

设靶翼角z0＝0时，即高控系统不工作状态下，对应的拖靶飞行高度为H0，

相应的，设H0处拖缆拉力的垂直分量为TH0，

则 TH0＝ mg，

设HL处拖缆拉力的垂直分量为THL

那么基于线性假设，对于靶高H处，拖缆拉力的垂直分量

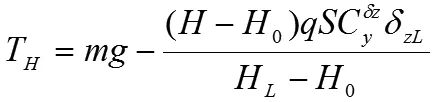
2.2 计算升力L

由于拖靶飞行时的攻角很小，而且拖靶的气动外形基本为上下对称，所以靶体和尾翼的升力可以忽略不计，即拖靶的升力主要来自舵翼。根据飞行力学的原理，升力的计算公式为

2.3 计算Dy

气动阻力的垂直分量与垂向速度有关。设拖靶的水平速度为vx，由于拖靶飞行的静稳定性较大，当拖靶具有垂向速度时，拖靶能够迅速使迎角变为零，即对垂向速度的阻尼主要来自气动阻力在垂向上的分量。因为垂向速度为 Hvy˙= ,则速度方向与水平面的夹角为

则有

阻力DqSCD= ，其中CD为拖靶的阻力系数。

由于在拖靶的超低空飞行阶段，拖靶的水平速度Vx是基本恒定的，所以可以认为拖靶受到的空气阻力的垂直分量与垂向速度成正比。

2.4 建立微分方程

将上述的计算结果代入到微分方程中，可以得到

在平衡点附近，上面微分方程中的系数可以认为是常数，这样就得到了一个线性化的数学模型，从而可以采用经典的线性系统理论来进行控制律的设计。

3 传递函数的确定

对拖靶的线性化模型采用Laplace变换进行处理，即用各个系数在拖靶飞行的平衡工作点处的值来近似代替实际值，然后对该微分方程进行拉氏变换，就可得到系统的传递函数。根据Laplace变换的特性，可以得到

即

即可得到：

从舵翼角z到高度H的传递函数

从零位舵翼角高度H0到高度H的传递函数

4 结束语

拖靶的垂向运动传递函数是设计拖靶高度控制系统的基础。以拖靶为研究对象，通过受力分析，得到拖靶的垂向运动微分方程，再根据线性系统理论中的小扰动假设，就能够从静态出发，研究平衡点附近的动态特性。应用这种方法，在拖靶的设计阶段得到的传递函数，为拖靶高度控制系统的设计提供了定量分析的手段，对其设计工作意义重大，为分析实际拖靶的飞行状态提供了重要的工具。

[1] 王一飞.TW-1拖靶缆绳张力与形状参数的计算. 南京航空学院学报，1992

[2] 胡寿松.自动控制原理. 科学出版社，2001

[3] 吴森堂.飞行控制系统. 北京航空航天大学出版社，2005

[4] 方振平.航空飞行器飞行动力学. 北京航空航天大学出版社，2005