山区铁路越岭选线几何模型的探讨
曾加胤
(中铁二院工程集团有限责任公司,四川成都610031)
1 研究的背景
1.1 地形背景
我国地形主要分为五大基本类别:平原、盆地、丘陵、山地、高原。其中山地面积占全国面积的2/3,山地崎岖,交通建设难度大。而在山地地形中,从平原、盆地向高原过渡段的山地地形较为复杂。伴随着我国社会经济的发展,山区交通建设迎来了春天,而作为经济先行的交通骨干,山区铁路建设逐年增加,山区铁路选线设计越来越复杂。
1.2 工程需要
依托地形和地势选线是山区铁路选线基本原则之一,在崎岖的山地选线中如何利用地形选线成为选线工作的主要任务。除考虑铁路经由经济据点的站点设置,往往需穿越山脉,解决越岭问题往往成为选线工作的关键。
2 几何建模
2.1 问题的提出
拉林铁路桑日至加查段线路方案比选中,经曲松方案需翻越海拔5 000m的步当拉山,是一段典型的越岭线路。经曲松越岭方案如图1所示。

图1 经曲松越岭方案
基本任务:经曲松方案从加查(海拔3260m)站引出后沿S306前行,展线越岭步当拉山,下山至桑日(海拔3577m),铁路限制坡度12‰。
2.2 建模分析
紧坡越岭地段,理想的线路是每一段线路用足坡度向着目标方向迈进。山区铁路所经地形由大、小的山岭和山谷构成,选线控制点为最大的山岭和最深的山谷。理想的线路所有的越岭和跨谷前后地形顺线路方向自然坡率均不大于限制坡度。
选取典型:首先需要整体分析焦点山体(全线大、小的山岭与山谷均有相似性),抽取山体模型如图2所示。本段线路最困难、最控制线路的山岭是步当拉山。通过步当拉山最极端方案是展线至山顶或特长隧道通过,而实际上采纳的往往是展线与越岭隧道相结合方案。
工程极限:工程能力是人类改造自然的能力和手段,它是有极限的。在该线工期控制下隧道单面坡长度最大约14 km,桥梁受抗震烈度控制,最大墩高不宜高于50m。结合山形(地面线)该参数直接控制了越岭及山谷线路极限标高。
经济参数:从理论上讲,不计成本展线总可以到山顶。从工程费用、运营维护费用来综合考核,单位长度隧道工程相当于N倍单位长度路基工程(比如在某工程上N≈2.5)。能实现通过障碍物的路基方式、隧道方式比较中,路、隧长度比大于N时,路基方式不经济,反之则路基方式较经济。
展线的代价:理论上,从A点到B点,凡是比理想的线路长的线路都存在工程及运营浪费,线路在A-B连线某点P上线路高程(如越岭隧道进出口)若高于理论最大Hth=Lpr×imax(Hth为理论线路可达高度,Lpro为A-B连线投影长度,imax为扣除折减后最大有效坡度),线路产生超拔起高度,线路展长浪费段不小于(HP-Hth)/imax。如图2所示。
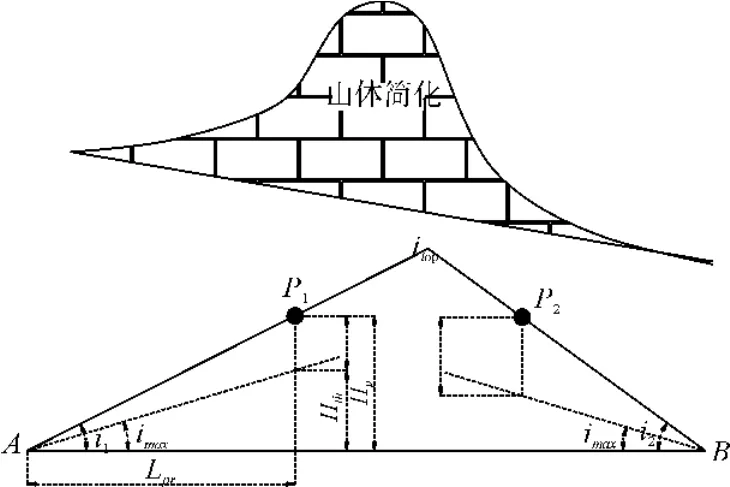
山体坡度:建立山体模型如图2所示,越岭两侧山体计算坡率分别为i1、i2,是山体两侧的抽象坡率。
越岭判断:越岭地形通常分为台阶地形、锯齿地形、凸地形三种。以凸形地形为例,理论上通过山体的两种方式,以隧道方式通过线路长度为Ltun(Ltun是隧道长度≈Lpr),硬以路基方式展线通过理论上最短线路长度为Lbed=(L1×i1+L2×i2)/imax(路基长度Lbed)。以山体左侧部分来分析,Ltun=L1,展开长度 LZ=L1×i1/imax,当 Lbed/Ltun>N(即 i1/imax>N)时,采用隧道方式越岭要经济。理论上i1/imax>N,越岭隧道口高度越低,在山脚越岭,展线越短,但该最低标高受隧道极限工程长度控制。
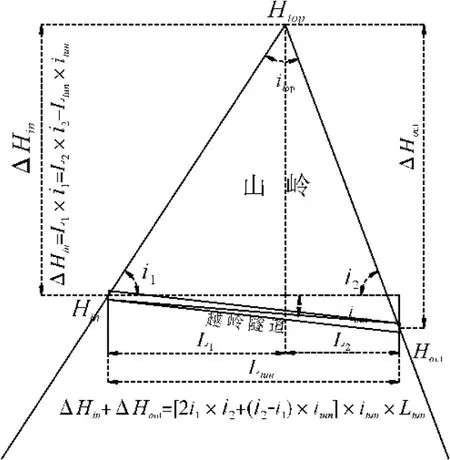
图3 山体几何简模
越岭坡度:越岭两隧道口距山顶高差总和越大,线路超拔起总高度越小,山岭两侧展线总和越短,如图3。ΔHin+ΔHout=2L1×i1+Ltun×itun,其中 L1=Ltun×(i2-itun)/(i2+i1),故ΔHin+ΔHout=[2i1×i2+(i2-i1)×itun]×itun×Ltun,从公式可以看出,高程极度困难越岭条件下,隧道坡度itun取极限坡度imax时,Ltun采用工程极限长度Lmax时,越岭隧道以极限坡度整体展线浪费最小。而山体两侧来看,当i2>i1(相反的越岭方向差值2(i2-i1)×itun×itun×Ltun)从地形陡峭侧(坡度最紧)爬至地形相对平缓侧时,整体展线长度较小。
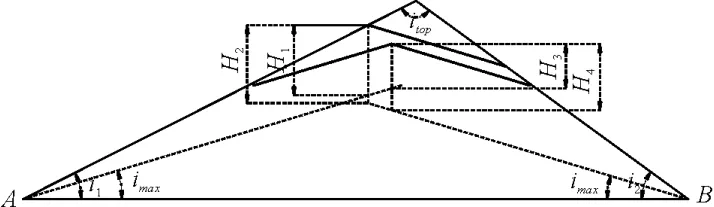
图4 人字坡隧道Lmax增长
人字坡优劣:使用人字坡后,两隧道口连线实际坡度itun<imax,同等的隧道投影长度Lmax,根据前述公式,两隧道口线路拔起高度之和不能达到最小,故理论上人字坡比单面坡展线浪费大。但如图4所示,人字坡隧道排水便利,可以双面掘进,如果仅受工期控制,人字坡隧道理论极限长度为2Lmax。当山体两侧都比较陡峭(Lbed/Ltun>N)设隧道经济时,用人字坡有助于减少整体展线长度。但台阶地形陡峭侧Lbed/Ltun>N,另外一侧山体 Lbed/Ltun<N(或 i1<imax)无需设隧道,只有一侧值得设隧,故台阶地形使用单面坡要优。
越岭部位:公式 ΔHin+ΔHout=[2i1×i2+(i2-i1)×itun]×itun×Ltun=[itun×i2+(2i2-itun)×i1]×itun×Ltun,工程极限能力一旦确定后,越岭隧道长度Ltun及坡度itun均基本确定,山岭两侧地形越陡峭,i2与i1越大,互补的顶角i顶越小,整体展线越小,故我们尽量选择最深凹的部位越岭,常见的是鞍部、洼地、山谷。
越岭标高:理论高位隧道口 Hhigh=Htop-L1×i1=Htop-i1×(i2-itun)×Ltun/(i2+i1)
理论低位隧道口 Hlow=Htop-(L1×i1+Ltun×itun)=Htop-i2×(i1+itun)×Ltun/(i2+i1)
3 模型的应用
将上述模型应用于拉林铁路桑日至加查段经曲松越岭方案。
3.1 越岭
实际山体并非圆锥体,其纵切面并非三角形,前述理论分析基于对山体的实际外形主要特征的抽象简化。该数学模型在定性分析上更具实际意义。

图5 经曲松方案纵坡
定性指导:如图5所示,从全段模型来看,桑日至山顶、加查至山顶连线坡度分别为24.9‰、28.6‰均大于12‰(实控约10‰左右),宏观判断需展线或越岭。最困难、最典型的步当拉山岭顺线路方向坡度西麓和东麓地形坡度分别为112‰、227‰,按上述数学模型为指导,展线后理论上最短线路长度为112×Ltun/12、227×Ltun/12,远大于路隧比N值,从理论上定性需越岭设计。步当拉山岭桑日侧坡脚地形坡度5‰(i1<imax),加查侧坡脚则较陡(Lbed/Ltun>N),判断为台阶地形,适合单面坡隧道作越岭设计。山体东麓比西麓陡峭,隧道以imax(考虑困难条件隧道折减0.93×12‰=11.16‰)坡度从东麓爬向西麓,以极限长度隧道Lmax(单面坡长约14 km)来控制越岭点标高。
寻找凹槽:山体通常分为山顶、山脊、鞍部、山谷、洼地几个部分,山顶、山脊线较适合微丘地形,对崎岖的越岭地形显然不适。据前面模型分析,山体凹槽(鞍部、山谷、洼地)从山顶到越岭隧道口连线的坡度最大,是越岭选线的首选位置,我们应选择最深凹槽。崎岖的山地千沟万壑、千棱万角,难以快速寻到鞍部、主谷及山顶。由于该线地形大小凹槽密布层叠,难以判别,笔者经比选将毗邻的无效凹槽擦除标记,仅留几个有争议的待选凹槽,有助于我们早日锁定目标。
毗邻的凹槽容易选择,但位置不同但有相近深切度或者偏离线路方向更深的凹槽如何应用上述模型?需要据越岭两侧备选凹槽共同确定,一般经验是与线路目标方向上夹角最小的凹槽又是更有效凹槽。对共同的越岭终点,不同的越岭起点凹槽,可以通过比较线路方向山顶与越岭起终点凹槽连线山顶角itop大小,或通过起终点凹槽连线距离(itop对应的边)大小来判别,山顶角越小,越岭凹槽部位越优。
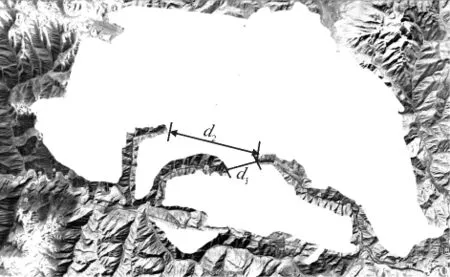
图6 排除无效凹槽
筛选剔除大量无效凹槽,寻找主要备选凹槽,最终确定越岭凹槽如图6所示。以最大限坡11.2‰,14 km隧道长度来切合山岭地形确定隧道进出口位置,从山顶往山脚定线。
3.2 展线
解决最大越岭问题后,越岭隧道低位拉索(3761m)与加查(3259m)高差502m,其直线距离22.1 km,连线坡率22.7‰,是有效限坡(据统计约为9.8‰)的2倍以上,初步分析线路需展长一倍以上(线路牺牲在争取高程之中)。
展线有了指导长度,还需根据实际条件合理布局展线。这些条件通常有展线段山势坡度变化(当然还有地质、水文、隧道通风等常见因素)、线型走势、最小半径、车站长度要求,展线要顺地势、布站位、顺线势。
顺地势:山坡地形从山脚到山顶通常是先缓后陡。任取线路上一段分析如图7所示,在线路行进中的某一段山坡可以粗略抽象为一段斜面,其与水平面夹角为θmou,铁路与该斜面的水平线名义夹角为θrail,铁路与水平面真夹角为θpro,sinθpro=sinθrail×sinθmou,当铁路以最大限坡 i限展线时,某坡段sinθpro为和sinθmou为定值,可以计算展线角度理论指导值θ向。根据上式,不同坡段 θpro为定值,当 θmou越大,θrail越小,理论上讲,地形越陡峭地段需集中展线。
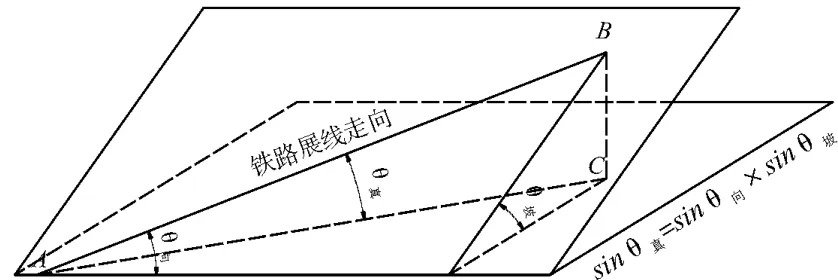
图7 展线模型
S306越岭陡峭段集中展线实例如图8所示,铁路展线同样需要在靠近越岭隧道口处更密集地展线来顺应地势,力所能及地减少长隧、高桥。

图8 陡坡集中展线
布站位:单线铁路行车要求站间距一般不大于15 km,坡度小且一般不宜在隧道内,进一步限制了展线长度,故选择合适的地形和里程合理布局站位是展线工作的重点。
顺线势:当站位布局好后,往线路方向左侧还是右侧展线要顺线势。一般往两站直线夹角钝角方向展线,以求最大的展线空间,减小曲线吃掉车站直线的长度。顺线势还要求展线段与两站夹角基本均衡,要满足最小曲线半径展线要求。本线最小半径1 600m(非空间圆,铁路要求圆曲线平面投影成圆),展线一个回头通常是10 km以上,展线(如果不后退)前进大于3.2 km,线形要求极大限制了展线的自由度。
地势、站间距、线型要求已经将该段展线限制到最困难的边缘,如下图9所示。
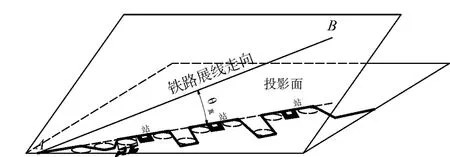
图9 展线限制
3.3 结果
如图1和图5所示,经曲松方案从加查站引出后沿S306前行,S型展线经班达、犹如拉至越岭前最高点拉索站,以15.6 km(单面坡13.7 km)长隧越步当拉山至线路最高点曲松,完成越岭过程下山至桑日。
4 模型的拓展
将山岭地形倒过来就是山谷地形,越岭模型倒过来就是山谷、洼地,隧道长度极限转变为桥跨极限,将越岭模型翻转90°就是穿越平面障碍物模型。桥跨极限能力较短,平面跨越障碍物不受铁路坡率影响,公式中限坡参数影响小,这里几何模型的指导作用还在于以一种统一的视角看待多种地形。
受板块挤压显著影响,川藏(四川西部、西藏南部)连接地段为庞大连片山脉,以南北走向为主的千沟万壑、山高谷深陡峭地形,经济据点处沟谷之中,最缓的凹槽自然成为汇水区,其汇水冲刷下自然形成了大江、大川。川藏地段大江、大川南北走向与线路东西走向不一致,难以借助大江、大川多年切缓的凹槽。若平面上绕避这些高山深谷,向北部山谷上游展线即走向高原面(青藏铁路),也与线路走向不一致,展线代价过大,失去了走向意义。以统一的几何视角来看待这种地形,经济据点间非孤立的山体在平面上是无法绕避,必须越岭、跨谷。凭桥梁数以百米计、隧道数以十公里计的极限参数,线路必受深谷所制,长隧相连。
5 结论
铁路有线形要求,铁路工程实现的基础是各种天然混成的大地,无论是委屈线形以适应地形的展线,还是以工程克服地形越岭、跨越天堑来改善线形都是有底线的。线形需满足行车要求,工程手段是有极限的,如何协调地形与线形的矛盾,如何使线势与地势相结合,几何模型以科学的论证给选线工作提供了分析的基础。
[1] 林世金.线路设计方案常见问题剖析∥[G].中铁二院技术委员会线路、轨道专委会2011年会论文集.成都:中铁二院工程集团有限责任公司,2011
[2] 易思蓉.铁路选线设计(第三版)[M].成都:西南交通大学出版社,2009
[3] 郝瀛.铁道工程[M].北京:中国铁道出版社,2000

