基于AWE的陶粒混凝土砌块切割机主轴的分析与优化

韩立光，秦宝荣，赵海宝，王淑花

(特种装备制造与先进加工技术教育部/浙江省重点实验室(浙江工业大学)，浙江杭州 310014)

基于AWE的陶粒混凝土砌块切割机主轴的分析与优化

韩立光，秦宝荣，赵海宝，王淑花

(特种装备制造与先进加工技术教育部/浙江省重点实验室(浙江工业大学)，浙江杭州 310014)

建立了陶粒混凝土砌块切割机主轴的三维模型，通过AWE软件对其进行了有限元分析，得到锯片轴最大应力、变形及其分布情况，并对其进行模态分析，提取其前几阶自然频率及振型，然后根据分析结果对锯片轴进行了结构优化，得到最优结构参数，为锯片轴的设计提供了理论依据。

陶粒混凝土砌块;切割机主轴;有限元分析;优化设计

陶粒混凝土砌块是一种符合国家建筑节能要求的新型自保温墙体材料。砌块采用模具成型，金刚石圆锯切割的成型方法［1］。由于砌块成分复杂，切割过程中锯切力复杂多变。切割机主轴作为金刚石圆盘锯的关键部件，直接承受切割弧区传来的锯切交变载荷和驱动扭矩，其应力分布、变形程度以及振动特性直接决定着整机运行的平稳性，砌块的表面加工质量及锯片的使用寿命等［2］。因此，确定切割机主轴在锯切过程中的最大应力、最大变形及其分布位置、固有频率和振型，并在此基础上进行优化设计，对降低生产成本，提高经济效益有一定意义。

本文借助 ANSYS Workbench 软件［3］，通过模拟切割过程的实际工况，对砌块切割机主轴进行有限元分析，得到主轴最大应力值和变形量及其分布云图。通过模态分析确定了其前几阶固有频率和振型，并在此基础上以主轴质量、最大应力和最大变形为目标函数，实现了对主轴的优化［4］。

1 切割机主轴模型的建立

1.1 锯片驱动、安装方法

本文设计的砌块切割机锯片驱动、安装结构图如图1所示。

图1中锯片6、间隔部件7通过销轴5与驱动部件4连接，驱动部件4通过平键与锯片轴连接，锯片轴通过支承2固定于支承座1内，减速电机带动锯片轴转动，从而实现锯片切割扭矩的传递。

锯切过程中，锯片轴在锯片安装部位承受切割弧区坯料对锯片的进给压力;驱动部件安装部位承受锯切阻力产生的阻力矩，锯片匀速转动，阻力矩与减速电机的输入扭矩平衡。

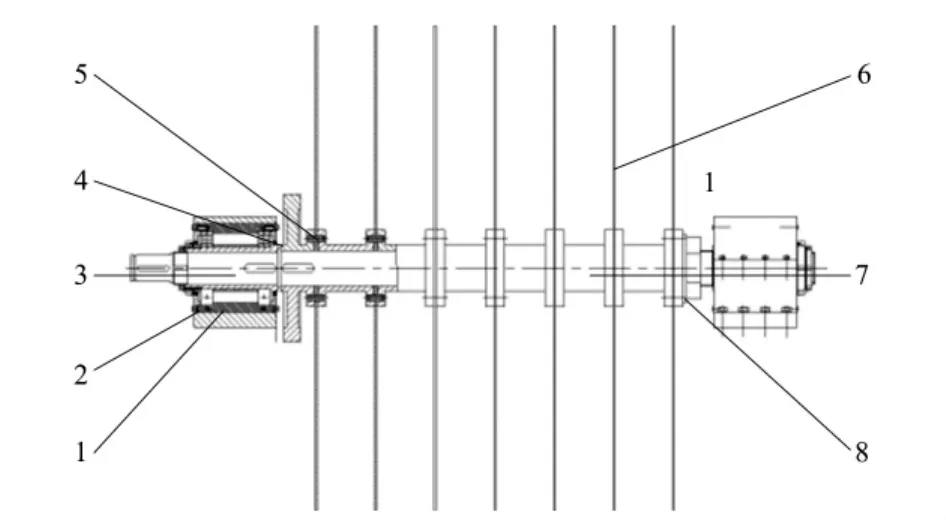
图1 锯片安装结构图

1.2 切割机主轴受力分析

锯切过程中，锯片轴直接承受锯片切割砌块坯料产生的锯切反力和减速电机输入的扭转力矩。混凝土锯切与磨削尤其是蠕动磨削类似，锯切力可以分解为法向力Fni和切向力Fti。根据磨削力的经验公式［5］:

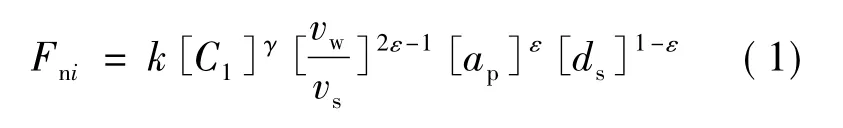
式中:切削深度 ap=600mm，锯片直径 ds=1 600mm。据现场生产经验知:进给速度 vw=325mm/min，锯片转速 n=479r/min，电机功率P=45kW，切割速度 vs=2πnds/2=40m/s。根据 Mamalis［6］提供的数据: ε =0.6，k［C1］γ=61N/mm2，代入式(1)、(2)中可得:Fni=1 268.8N，Fti=159.8N。

将锯片所受锯切反力等效转换为轴心处的一对力(Fni和Fti)和附加力矩，将附加力矩进行叠加，即锯片轴在驱动部件安装部位受到的阻力矩T2，其与减速电机的输入扭矩中T1互为一对平衡力矩，故有T2=T1=9 550P/n=897.2N·m，转换为对键槽侧面的压力为17.48MPa。锯片轴受力示意图如图2所示。

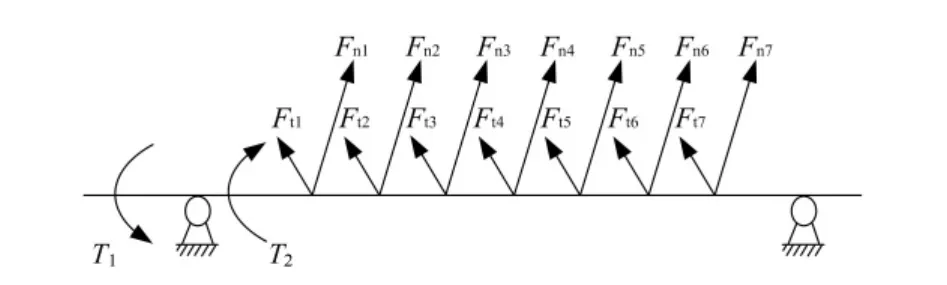
图2 切割机主轴受力示意图

1.3 主轴有限元模型的建立

分析过程中，忽略对分析结果没有实质性影响的几何特征，保留驱动部件处的键槽。在CAD软件中建模并导入DM平台，在锯片安装部位、支承位置处轴表面进行Imprint face分割。

主轴的材料选用45#钢，其密度 ρ为7 800 kg/m3，弹性模量为 210GPa，泊松比为 0.3。整体采用Hex Dominant Method来划分六面体网格，单元大小设置为12mm，共生成147 562个节点和41 593个单元。

首先施加自重，在锯片安装表面施加Remote force(分量为Fni和Fti)，在锯片轴驱动部件安装部位键槽受力侧表面施加压力17.48MPa，支承部件施加圆柱约束，在扭矩输入表面施加全约束(如图3所示)。

2 分析结果及讨论

2.1 应力分析

在静力载荷作用下，主轴的最大应力发生在主轴与驱动部件连接键槽的受力面以及轴阶区域(如图4 所示)，最大值为32.942MPa，45#钢最小抗压强度 σb=375MPa，许用应力［σ］ = σb/1.5=250MPa。显然满足结构的强度要求，并且主轴有很大的质量冗余。

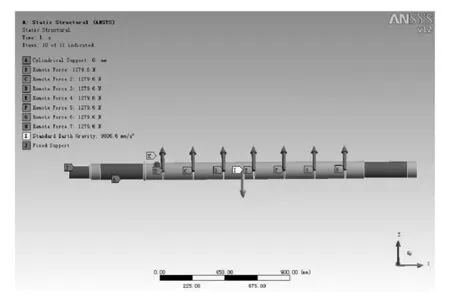
图3 主轴载荷及边界约束

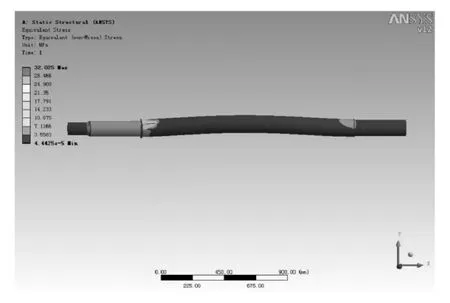
图4 主轴应力分布

2.2 变形分析

最大变形量出现在切割机主轴与锯片切割弧区对应侧的中间部位(如图5所示)，变形最大值为0.067 2mm，属于小变形，满足主轴的刚度要求。

图5 主轴变形分布

2.3 主轴模态分析

不考虑主轴的受载情况，只保留其位移约束条件。由于倒角、螺纹、键槽等特征对主轴的质量影响甚微，因此忽略其对模态的影响。主轴的低阶模态对其性能影响较大［7］，故只对其前6阶模态进行扩展，其自然频率和振型如图6所示。

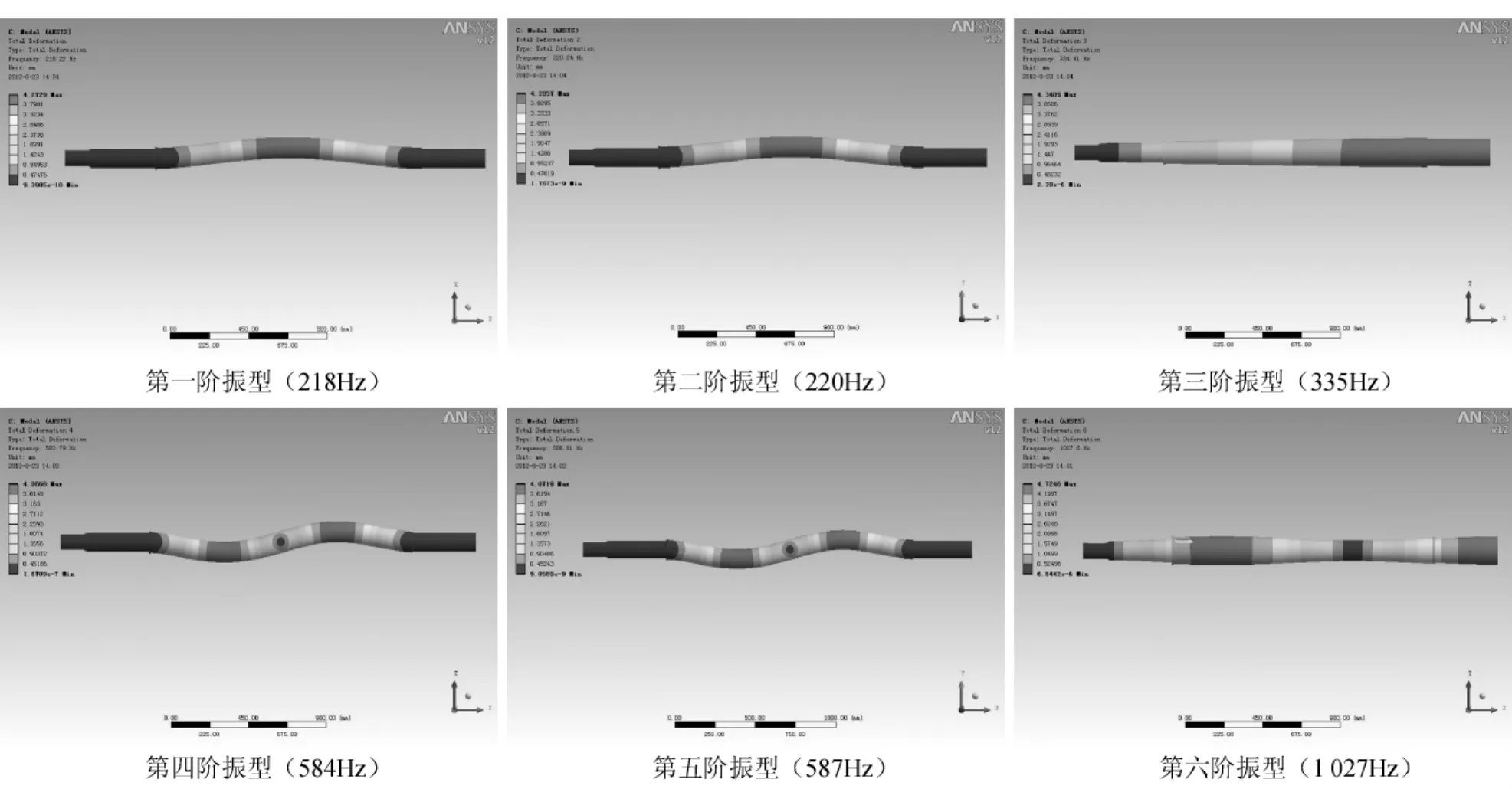
图6 锯片轴各阶振型

由图6可以看出，第一、二阶振型分别表现为锯片轴中间区域在XZ平面和XY平面内的弯曲变形;第三阶振型在非扭矩传入端主轴径向变形;第四、五阶振型分别表现为锯片安装区域在XZ平面和XY平面内的“S”形弯曲变形;第六阶振型表现为锯片轴在非动力输入端和驱动部件安装部位的径向变形。由上述分析发现:振动变形量较大的部位集中在锯片轴中间部位，在满足加工需求的情况下，减小主轴支承跨距是提高切割机床刚度和强度有效途径。本文中设计的切割机主轴转速为479r/min，减速电机工作频率在9Hz左右，距离主轴各低阶自然频率较远，故不会产生共振。

3 切割机主轴的优化设计

本设计的目的是在满足安装锯片部位挠度要求的条件下，使主轴质量最小［8－9］。选择对整体性能影响最大的主轴直径D、支承跨距L为设计变量，即设计变量为:

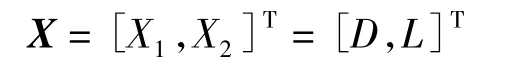
以锯片轴的质量为目标函数:

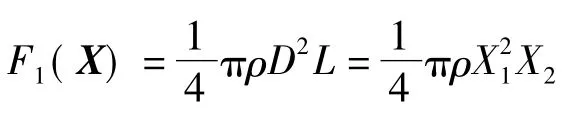
约束条件如下:

a.强度约束，切割机主轴在工作时应力不超过许用切应力［τ］。

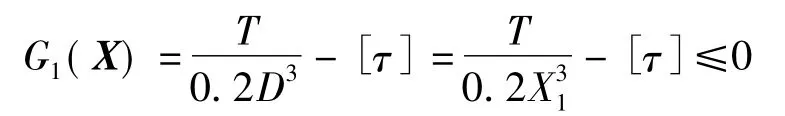
b.边界约束。

根据安装锯片以及支承处直径，选择主轴直径范围为90≤D≤150，也即90≤X1≤150。

根据主轴上所安装的锯片、驱动部件、间隔部件、锁紧螺母的结构尺寸，再考虑实际情况，最终选取跨距范围为2 240≤L≤2 600，也即2 240≤X2≤2 600。

优化结果为:锯片轴总变形量随轴径D和支承跨距L变化的响应曲面如图7所示，等效应力随轴径D和支承跨距L变化的响应曲面如图8所示，质量随轴径D和支承跨距L变化的响应曲面如图9所示。

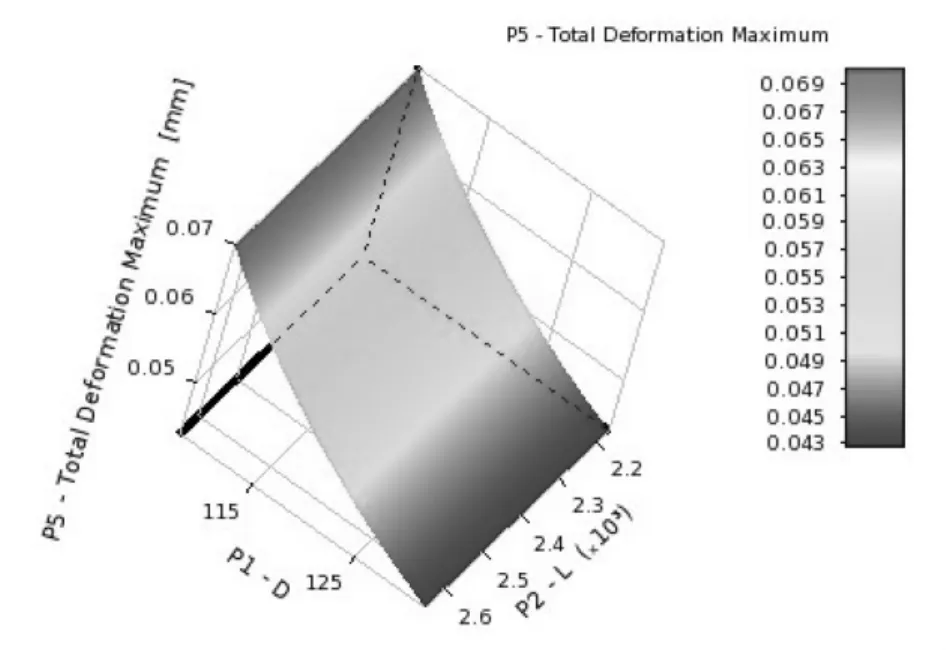
图7 总变形量随轴径D和支承跨距L的变化

由图7～图9可以看出，每个点对应一个直径D、支承跨距L和一个响应参数的值。从敏感度的角度可以看出，支承跨距L对变形的影响大于直径D的影响。

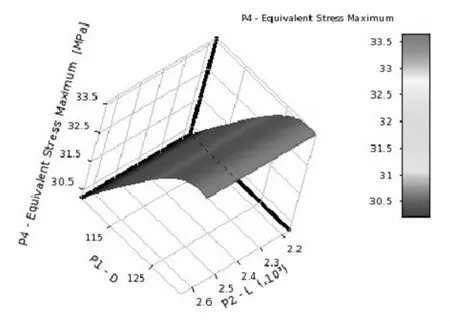
图8 等效应力随轴径D和支承跨距L的变化

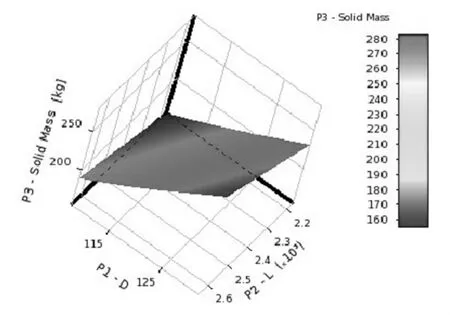
图9 质量随轴径D和支承跨距L的变化

通过设置目标函数的目标计算得到一组最优解。对最优解的参数进行修正并运行新的“Simulation”，优化前后参数及分析结果对比见表1。

由表1可知，优化后主轴的等效应力有所减小，其值为32.327MPa，总变形稍微有所增加，其值为0.067 9mm，主轴总质量减少近33kg。由此可见，基于AWE切割机主轴的优化设计，对切割机主轴的设计有一定的指导意义。

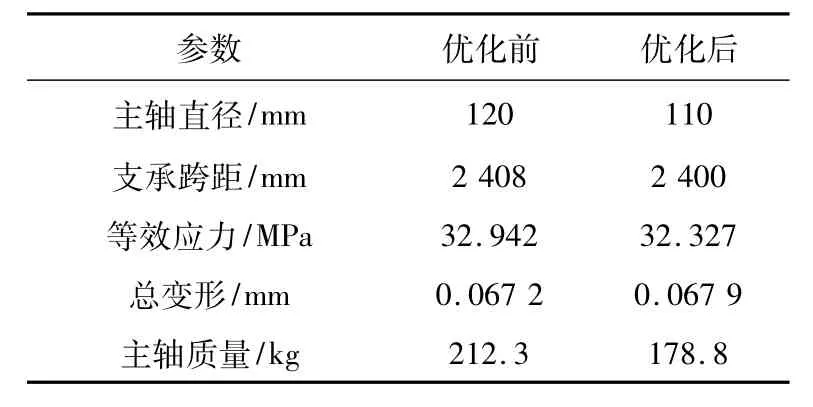
表1 优化前后结果对比

4 结束语

本文在理论锯切力的基础上，通过AWE软件对陶粒混凝土砌块切割机主轴进行了静力分析和模态分析，根据分析结果对锯片轴进行了结构优化，得到较为合理的结构参数，为锯片轴的结构设计提供了理论依据。锯片轴在实际工况载荷作用下的强度和刚度有待进一步的实验验证。

［1］范锦忠.陶粒泡沫混凝土砌块［J］.砖瓦，2009(7):44－49.

［2］黄文贤.石材机械主轴组件的设计(一)［J］.石材，2008(2):18－21.

［3］李兵，何正嘉，陈雪峰.ANSYS Workbench设计、仿真与优化［M］.北京:清华大学出版社，2011.

［4］陈龙，文湘隆，丁国平.基于有限元分析的轴的设计［J］.现代机械，2005(1):36－56.

［5］周灿丰，张宝生，曹建树，等.锯切力仿真与锯切参数选择［J］.金刚石与磨料磨具工程，2002(5):45－47.

［6］Mamalis A G，Schulze R，Tonshof H K.The slotting of blocks of hard rock with a diamond segmented circular saw blade［J］.Industrial Diamond Review，1979(10):356－365.

［7］张耀满，王旭东，蔡光起，等.高速机床有限元分析及其动态性能试验［J］.组合机床与自动化加工技术，2004(4):48－50.

［8］吴化勇.机床主轴部件有限元分析及优化设计［J］.机床与液压，2008(11):158－159.

［9］裴大明，冯平法，郁鼎文.基于有限元法的主轴轴承跨距优化［J］.机械设计与制造，2005(10):44－46.

Analysis and Optimization of the Spindle of Ceramisite-reinforced Concrete Block Cutting Machine Based on AWE

HAN Liguang，QIN Baorong，ZHAO Haibao，WANG Shuhua
(Zhejiang University of Technology，Zhejiang Hangzhou，310014，China)

It establishes 3D model of the spindle of the concrete block special cutting machine.Based on software of AWE，it realizes the finite element analysis and obtaines the maximum stress，strain and the distribution.In view of the shaft modal analysis，it desceibes the low order inherent vibration frequencies and modes，applies the goal-driven optimization method in the optimal design of the spindle，it shows the optimal structure parameters.This provides the reliable theory reference for the spindle＇s design.

Ceramisite-reinforced Concrete Block;Spindle;Finite Element Analysis;Optimization

TH122

A

2095－509X(2013)02－0006－04

10.3969/j.issn.2095 －509X.2013.02.002

2012－09－03

韩立光(1986—)，男，河南周口人，浙江工业大学硕士研究生，主要研究方向为机械设计。