基于压缩感知理论的图像压缩技术研究

王辛悦，周德全

(浙江农林大学信息工程学院，杭州 临安 311300)

1 引言

从外界获得的信息中，视觉信息占据了主导地位。而图像以其生动直观的特点以及包含的丰富信息，成为人们获得信息的主要工具。然而巨大的数据量给图像的传输和存储带来了极大不便，图像压缩技术显得尤为重要［1］。然而，在传统的压缩技术中采样遵循奈奎斯特定律，采样速率要高于原信号频率的两倍，这个过程浪费了大量的采样资源，加大了计算复杂度，也造成了不必要的内存浪费。而相较之下，近年来信号处理领域诞生的一种新的信号处理理论—压缩感知理论［2-4］，针对可稀疏表示的信号，能够将数据采集和数据压缩合二为一，降低了计算复杂度，避免了不必要的空间浪费，这使其在信号处理领域有着突出的优点和广阔的应用前景。

压缩感知采用非自适应性投影来保持信号的原始结构，能够通过数值最优化问题准确重构原始信号。压缩感知理论主要包括信号的稀疏表示、随机测量和重构算法等三个方面。稀疏表示是应用压缩感知的先验条件，随机测量是压缩感知的关键过程，重构算法是获取最终结果的必要手段。

2 压缩感知理论

2.1 稀疏性

一般的自然信号X∈RN本身并不是稀疏信号，但一般可以在某种稀疏基上进行稀疏表示，即:

其中，S为信号的稀疏系数。信号的稀疏表示就是将信号x投影到正交变换基Ψ时，大部分变换系数的绝对值近似为0，所得到的变换向量S是稀疏的或者近似稀疏的［2］。则压缩感知方程为:y=Ø×x=Ø×Ψ×s=Θ×s。通过该变换可将原来的测量矩阵Φ变换为传感矩阵Θ=Ø×Ψ，解出s的逼近值Ŝ，则原信号x^=Ψ×ŝ，从而实现了信号x的稀疏表示。

2.2 测量矩阵设计

根据压缩感知理论，通过变换得到信号的稀疏系数后，需要设计压缩采样系统的观测部分，它围绕观测矩阵Φ展开。测量过程可以表示为

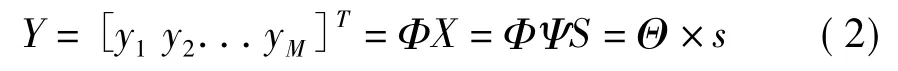
其中，Y为M维观测向量，Φ为M×N维的观测矩阵。但要想使信号完全重构，必须保证观测矩阵不会把两个不同的K项稀疏信号映射到同一个采样集合中，这就要求从观测矩阵中抽取的每M个列向量构成的矩阵是非奇异的。测量矩阵要满足三个特征:①由测量矩阵的列向量组成的子矩阵的最小奇异值必须大于一定的常数;②测量矩阵的列向量体现某种类似噪声的独立随机性;③满足稀疏度的解是满足1范数最小的向量。独立同分布的高斯随机测量矩阵可以成为普适的压缩感知测量矩阵。但是，它在硬件实现和重建算法构造上却难以实用。相对高斯矩阵等硬件上较难实现的其他随机矩阵形式，伯努利分布的±1矩阵成为构建硬件可实现的压缩感知方式的首选。

2.3 重构算法

设X∈RN的稀疏度为K，Φ为M×N的二维矩阵(K＜M≪N)，Y=Φ×X为长度M的一维测量值。压缩感知重构问题就是在已知测量值Y和测量矩阵Φ的基础上，求解方程组Y=Φ×X，得到原信号X。需要求解如下最优化问题［5-6］:

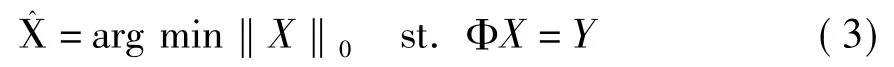
这个过程称之为重构，式中‖X‖0为0范数。该优化问题属于NP难题，一般转化为，

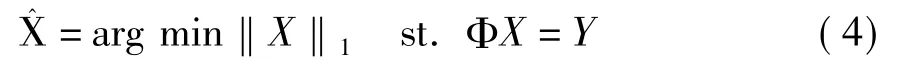
求解。常用的优化方法有线性规划(BP)算法和匹配追踪算法［7］或正交匹配追踪算法(OMP)［8］等贪婪算法。要精确重构K稀疏信号X，测量次数M(即Y的维数)必须满足采样点数M=O(KlogN)的条件，并且矩阵Φ必须满足约束等距性条件。

3 正交匹配追踪算法

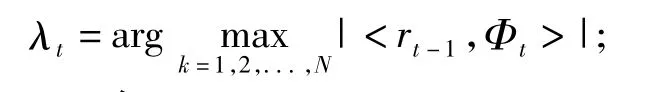
(3)令 Λt=Λt-1∪{λt};

(4)计算{λt:λ∈Λt}张成空间的正交投影Pt;

(5)计算新的近似a和冗余r:

(6)t=t+1，如果 t＜mt，则返回第(2)步;

(7)获得的估计Ŝλ在索引Λm位置的非零元，且在该位置的测量向量逼近为:

4 实验结果

目前基于CS理论的重建算法主要分成四类:凸优化方法、组合算法、统计优化方法和贪婪算法。贪婪算法是4类算法中重建速度最快的算法。另外，在CS理论中，由于图像重建过程可以看作已知信号在给定冗余字典上获得最稀疏分解的过程，而贪婪算法在信号稀疏化中的应用较为成熟。现准备利用OMP算法重构图像。OMP算法通过递归的对已选原子集合正交化求出正交投影Pt，利用rt=y-Pty的残差更新方式，克服了MP算法的次最优性。OMP算法为:

(1)初始化冗余向量r0=y，索引集合Λ0=Φ，迭代计数t=1;

(2)找到索引λ0，使得:

以256×256大小的8bit灰度lena图像做为原信号，首先利用式(2)对图像进行测量压缩，式(2)中的观测矩阵采用高斯随机矩阵，然后利用介绍的OMP算法重构图像。在测量率(测量值个数与原图像像素个数之比)分别为0.7、0.5、0.3 时，效果如图1所示。

图2给出了在不同测量率下重建图像的峰值信噪比(PSNR)值。由图2可知，当测量率过低时，PSNR的值相对较低，表明重建图像效果一般。仿真实验的结果表明，压缩感知理论应用于图像压缩领域是一项可行的技术。实际应用中，采用压缩感知理论进行抽样时，可直接对图像进行随机抽样，只需要得到少量的抽样值，并对抽样值进行量化编码就可以进行传输或存储。不必记录每个有效值的位置信息并对其进行编码，这大大降低了计算复杂度，也避免了不必要的空间浪费，最重要的是实现了低速采样。

图1 原图与重构图像

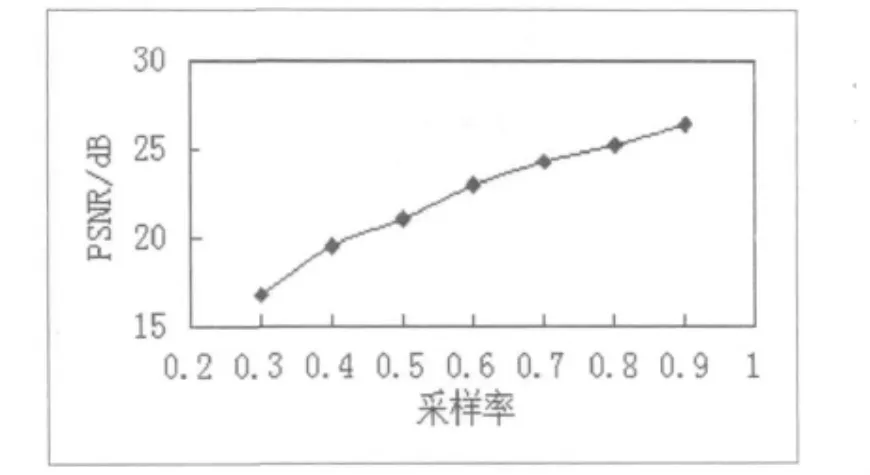
图2 psnr值与测量率的关系

5 结 束 语

主要介绍了cs理论用于信号压缩及重构时所涉及的信号稀疏表示、随机测量矩阵设计、信号重构算法三大核心问题。并给出了CS理论框架下的图像压缩与基于OMP算法的图像重构结果。通过对二维图像信号lean的实验证明压缩感知理论是一种测量值少而信号恢复准确的数据采集压缩理论，表明压缩感知理论在图像压缩方面具有重大意义。作为新兴理论，压缩感知理论的研究方兴未艾，将具有更加广泛的应用前景。

［1］覃风清.数字图像压缩综述［J］.宜宾学院学报，2006(6):88-90.

［2］Donoho D L.Compressed Sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［3］石光明，刘丹华，高大化，等.压缩感知理论及其研究进展［J］.电子学报，2009，37(5):1070-1081.

［4］Cands E.Compressive Sampling［C］.Proceedings of International Congress of Mathematicians， Madrid，Spain，European Mathematic Society，2006:1433-1452.

［5］Baraniuk R G.Compressive sensing［J］.IEEE Signal Processing Magazine，2007，24(4):118-121.

［6］RaVel C Gonzalez.Richard E Woods，数字图像处理［M］.北京:电子工业出版社，2010.

［7］Mallat S，Zhang Z.Matching pursuit with time-frequency dictionaries［J］.IEEE Transactions on Signal Processing，1993，41(12):3397-3415.

［8］Tropp J， GilbertA. Signalrecovery from random measurements via orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2007，53(12):4655-4666.