一种鲁棒非线性伺服控制器的参数化设计及应用

程国卿

(厦门大学嘉庚学院物流管理系，福建漳州 363105)

0 引言

在工业加工装配和物流自动化系统中，广泛采用伺服电机来作为驱动装置。在这类伺服应用中，控制系统发挥了关键的作用，使得系统具有快速、平稳的瞬态性能和稳态精确性［1-5］，其中瞬态性能关系到系统的运行效率和安全性。迄今，90%以上的工业控制系统采用PID控制技术［6］。PID的特点是简单易用，但它是一种单自由度的线性控制，难以实现快速响应与低超调，为此提出了非线性PID(如文献［7］)。为避免PID中的积分器饱和(Windup)现象，需加入抗饱和(Anti-Windup)措施(文献［8］)。这些改进方案增加了控制律的复杂度，偏离了PID原本简单明快的优点。文献［9］提出一种自抗扰控制(ADRC)，其主要思想是利用非线性微分跟踪器来提取导数信号和扰动估计值，采用非线性PD控制律来改进系统响应性能。但ADRC的闭环稳定性分析尚未解决，而且控制器参数很多，参数与系统性能之间的关系很难把握。

文献［10］提出一种线性反馈+非线性反馈的复合非线性控制方案，其中线性反馈使闭环系统具有快速的响应，而非线性反馈动态地调整闭环阻尼系数来抑制超调，使得系统具有快速且平稳的理想瞬态性能。文献［11］在此基础上给出了非线性反馈增益函数的参数优化整定方案，并在硬盘磁头定位伺服系统中得到了成功应用。但文献［10］和文献［11］都未考虑扰动因素的影响，当实际系统带有未知扰动时，将出现稳态误差，从而影响系统的控制精度。通常可以考虑引入积分控制来消除扰动的影响，但随之而来的是前述的积分饱和现象和瞬态性能恶化。本文在复合非线性控制的框架下，引入线性扩展状态观测器来同时估计系统未知状态和扰动，并用于补偿，以实现快速、平稳和准确的定点伺服跟踪，且对给定目标和扰动差异具有性能鲁棒性。这种控制器的设计过程中需要进行一些参数选择和矩阵求解，具有一定的难度。为简化设计和应用推广，本文针对典型的二阶系统模型，给出这种鲁棒非线性伺服控制器的一种通用的参数化设计方案，并用于永磁直线电机的调速系统中。通过MATLAB/Simulink仿真，验证了控制律的有效性和性能鲁棒性。

1 鲁棒非线性伺服控制器的参数化设计

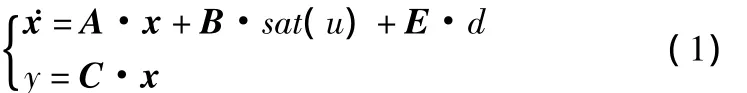
式中：x∈R2，u∈R，y∈R分别表示状态变量、控制输入、受控输出(可量测);d∈R为有界但未知的常值或慢变化的扰动;sat(u)表示饱和限幅函数，其定义如下：

式中umax表示控制量的最大允许值。假设系统模型满足以下条件：(A，B)能控;(A，C)能观;(A，B，C)和(A，E，C)在s=0处无零点。最后一个假设条件表示扰动d对系统稳态输出确实有影响，否则就不必考虑扰动补偿的问题。

典型二阶系统对应的模型矩阵如下：

按照模型的假设条件，有：

控制设计的任务是使输出y快速准确地跟踪给定的参考目标r。首先设计一个线性反馈控制律：

在控制律(2)作用下，系统闭环稳定，则当t→∞，有˙x(t)→0，x(t)→xss。其中xss是状态量x的稳态值。从式(1)和(2)可推导出：

高过滤是糖尿病肾病患者发病早期的特征性表现，是神经激素-血管及管球反馈机制综合作用的结果，ACEI等传统治疗药物对管球的反馈机制影响不大，因而不能完全改善高过滤对肾的损害。SGLT-2抑制剂可以通过管球反馈机制降低肾

系统输出y的稳态值为：

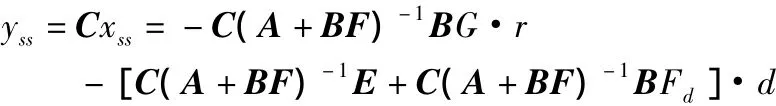
由于控制的目标是使输出y在有扰动的情况下能准确跟踪目标r，即：yss≡r，∀(r，d)，于是可求得：

下一步设计非线性反馈律，其作用是通过动态改变闭环阻尼来抑制超调量、从而提高系统的瞬态性能。选择一个正定的加权对角矩阵W为：

式中*代表矩阵的对称元素。则非线性反馈增益矩阵为：

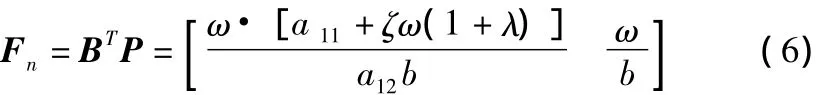
接着选取一个平滑的非线性函数ρ(r，y)≥0，它的值随着跟踪误差|r－y|的减少而增大，如：

式中α、β都为非负的可调参数。则非线性反馈律如下：

在控制律中用到了状态向量x和扰动d，它们通常并不全是可量测的，因而需要借助观测器技术来进行估计。考虑到扰动是常值或慢变化的，可用微分方程描述为˙d=0。把此方程结合到对象模型(1)中，得到增广后的模型：

基于状态观测器(9)，把式(2)和(8)的控制律合并起来，得到最终的鲁棒非线性控制律为：

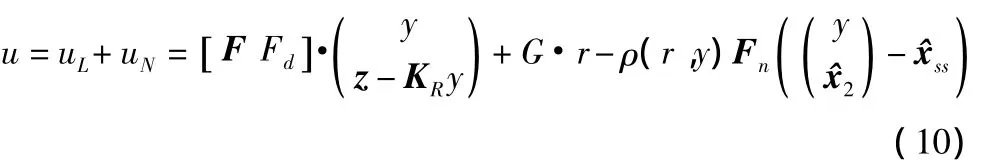
式中^xss是对状态变量x稳态值的实时估计，即：

控制律的参数值可按以下经验规则来选择：ζ∈［0.3，0.5］，ω = 预期的闭环带宽;ζ0∈［0.6，0.8］，ω0∈［3ω，6ω］，λ∈(0，1);非负参数 α、β 可通过仿真来整定，其中β可从0开始逐步增大至控制性能满意为止。上述参数化控制律可方便地应用于具体系统中，且有利于在线参数调优。根据文［10］基于根轨迹的分析，非线性反馈的作用将随着系统跟踪误差的减小而增强，使得闭环主导极点从初始位置逐步趋向于传递函数Fn(sI－A－BF)－1B的零点，即实轴上的－(1+λ)ζω和－∞(如图1所示)，从而动态地增大闭环阻尼来抑制超调、改善瞬态性能。

图1 闭环极点的轨迹

在扰动输入矩阵E未知的情况下，可把d当成等价输入扰动，即按E=B设计控制律。这时的控制律还能有所简化，且通常也可得到满意的性能。

2 永磁直线电机的速度控制

随着直线电机在工业和消费领域中的应用日益扩大，直线伺服控制已成为一个研究热点。本节利用鲁棒非线性伺服控制器来实现对直线电机速度的快速和准确控制。考虑常见的永磁同步交流直线电机，其在dq坐标系下的数学模型如下：

式中：ud，uq，id，iq分别是d、q轴的电压和电流，R为动子相电阻，L为d、q轴的电感值，v为直线电机运动速度(m/s)，τ为极距，ψf为定子基波磁势链过动子绕组的磁链，M为动子质量，Kb为粘滞摩擦系数，Kf为推力系数，FL为负载阻力(未知扰动)。采用id=0的矢量控制方式，以速度v作为系统的受控输出量(可量测)，交轴电压uq作为控制输入量，可把以上模型转化式(1)所示的二阶系统，对应的状态变量和模型参数为：

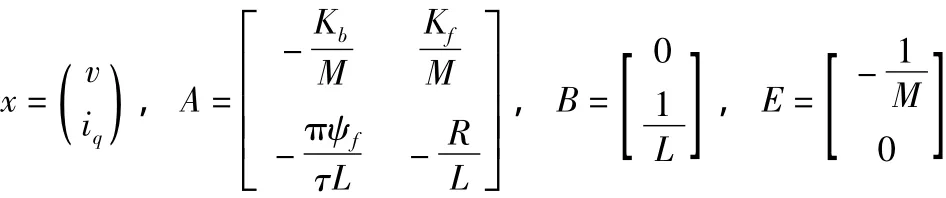
以文［4］中的直线电机作为被控对象，假定其q轴电压最大值为Uqmax=180V，其它参数为：

把前一节设计的参数化控制律(式9～11)直接用于该电机的速度控制(不需测量电流信号)。在MATLAB中进行仿真研究，选取控制参数值如下：

图2 仿真结果(标称情况)

图3 仿真结果(电机参数变化)

3 结束语

提出了一种面向典型二阶伺服系统的参数化鲁棒非线性控制律，并用于永磁直线电机的速度控制。控制律以线性+非线性的复合反馈控制为基础，利用扩展状态观测器来估计系统状态和扰动信号并进行补偿。在MATLAB/Simulink中进行了仿真研究。结果表明：提出的控制方案可以实现快速、平稳和准确的定点跟踪控制，且对负载扰动和参数变化具有较好的鲁棒性。这种参数化控制律具有通用性，可推广到其他伺服系统。

［1］马素君，谢武斌.基于RBF神经网络的永磁同步直线电机全局滑模控制［J］.组合机床与自动化加工技术，2012(7)：82 －84，88.

［2］程有龙，刘栋，张东升，等.精密伺服进给平台控制系统设计［J］.组合机床与自动化加工技术，2011(6)：41－43.

［3］王丽梅，陈吉超，郑浩.基于滑模和重复控制的永磁直线同步电机控制［J］.组合机床与自动化加工技术，2011(4)：51－54.

［4］蓝益鹏，王雷，张琳琳.CAK6163Di数控车床直线电动机直接驱动系统模糊自适应控制的研究［J］.组合机床与自动化加工技术，2009(9)：70－72.

［5］张霖，党选举，曾思霖.永磁同步直线伺服系统的一种双模控制［J］.电气传动，2010，40(2)：53－56.

［6］ANG K H，CHONG G，LI Y.PID control system analysis，design，and technology［J］.IEEE Transactions on Control Systems Technology，2005，13(4)：559 －576.

［7］HEERTJES M，SCHUURBIERS X，NIJMEIJER H.Performance－improved design of N－PID controlled motion systems with applications to wafer stages.IEEE Transactions on Industrial Electronics，2009，56(5)：1347 －1355.

［8］CHOI J.-W.，LEE S.-C.Anti-windup strategy for PI-type speed controller［J］.IEEE Transactions on Industrial Electronics，2009，56(6)：2039 －2046.

［9］HAN JQ.From PID to active disturbance rejection control.IEEE Transactions on Industrial Electronics，2009，56(3)：900－906.

［10］CHEN B M，LEE T H，PENG K M et al.Composite nonlinear feedback control for linear systems with input saturation：theory and an application［J］.IEEE Transactions on Automatic Control，2003，48(3)：427 －439.

［11］LAN WY，THUM CK，CHEN BM.A hard disk drive servo system design using composite nonlinear feedback control with optimal nonlinear gain tuning methods［J］.IEEE Transactions on Industrial Electronics，2010，57(5)：1735 －1745.