模糊评判法在医疗设备采购评标定标中的应用

张 威 黄 泳 朱飞燕 曹 旭

模糊评判法是一种运用模糊数学的隶属度理论，对多种属性的事物进行多因素综合评价，把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价[1]。

医疗设备招标采购是我国政府采购的主要实施办法，目前评审专家在评标定标过程中，采取多种评标方法，但为了计算方便，普遍存在着将评审指标中定性指标人为地实行“强行”量化，忽略许多定性指标的模糊性，势必造成部分信息的损失，导致评定偏差。因此，只有将这些指标按照数学方法模糊量化，通过模糊评判法进行处理，才能更加科学、公平地评定中标单位[2]。

1 建立模糊评判的数学模型

(1)确定模糊综合评价因素集。评价因素集U是指被评价对象的n种因素组成的集合。即U={u1，u2，…，un}，在这里是投标书评标的指标体系集合(见表1)。

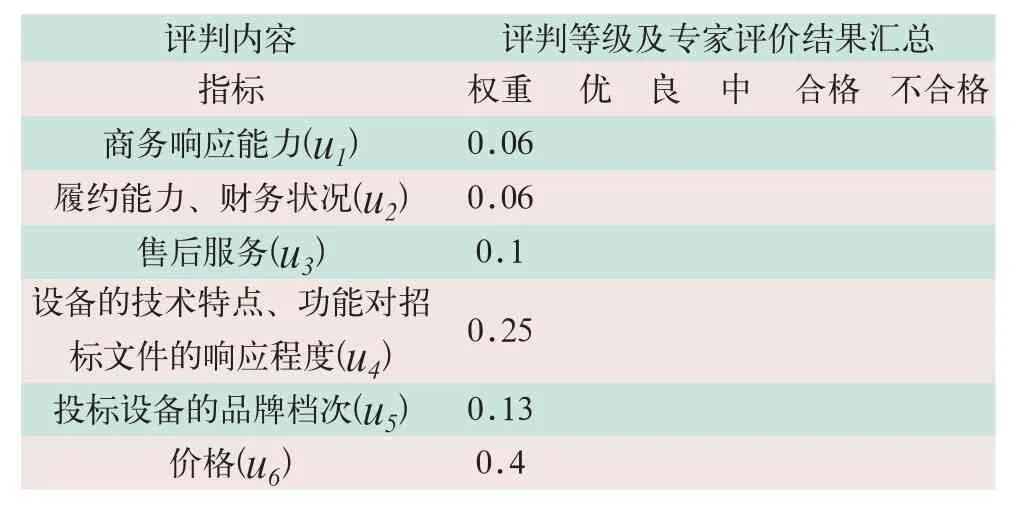
表1 评价指标体系集合表

(2)建立模糊综合评判等级评语集及权重向量。设V={v1，v2，…，vm}为刻画每一因素所有可能出现的m种决断，称为评语集，其实质是确定出被评价项属于各个评价等级的程度，这里使用“优，良，中，合格，不合格”5个等级作为评语集[3]。

权重向量A，A={a1，a2，…，an}，ai表示因素ui的重要程度，即分配到ui的权数，满足a1+a2+…+an=1，ai＞0。

(3)建立模糊评判矩阵。通过5位评标专家对3家投标公司的招投标书仔细查阅，对评判指标的内容进行模糊等级评定，以其中一家A投标单位评判结果为例，得到模糊评价矩阵[4-5]：

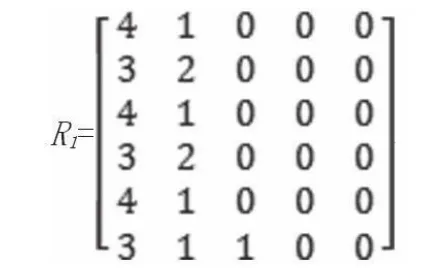
归一化后得到：

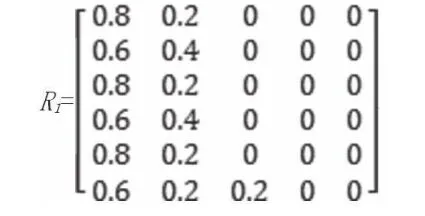
2 模糊评判计算

通过权重向量A与评判矩阵R的模糊变换得到模糊评判集B，即B=AOR={b1，b2，…，bn(公式1)，其中：

于是得到：

3 量化评判结果

评标的目的是从投标人中选出最优者，在实际评标工作中，用向量无法表示出投标人的评价结果，因此可以用一个“模糊数”来表示[6-10]。

一般利用隶属度，bi求综合分Y：Y=∑dkbk/∑bk，这里的dk是给定的等级参数，∑bk=1。对模糊综合评判等级评语集V赋予量化值(90，80，70，60，50)，则投标单位A的综合量化得分为：

同理，运用同样的方法计算出投标单位B、C的得分。YB=85.15，YC=85.21。3个投标单位按照分值顺序为A、C、B，A为第一中标候选人[11-14]。

4 结语

将模糊评判法引入医疗设备采购评标定标工作中，通过确立相应的模糊评判的数学模型，对模糊关系的计算，论证了该办法在评标定标中的可行性，为更加科学地评审提供了方法上的有力尝试[15-16]。

[1]孙福东,魏凤荣.应用excel巧解模糊综合评价法[J].统计与决策,2011(23):172-174.

[2]张凤毛.评标和定标的模糊评判法[J].山东科学,1998,11(3):16-18.

[3]黄耿鸿,伍燕青.基于模糊综合评价法的教学型实验室综合评价[J].实验室研究与探索,2011,30(8):376-378.

[4]郑蓓蓉,谢楠.模糊数学在实验室评估中的应用[J].温州大学学报,2001,14(2):56-58.

[5]曹久立,高传昌.基于VBA技术实现模糊综合评判法在EXCEL中的应用[J].华北水利水电学院学报,2007,28(6):48-50.

[6]张威,张晓伟,熊梦辉,等.关于提高仪器设备政府采购质量的思考[J].实验室研究与探索,2009,28(6):328-330.

[7]张威,张晓伟,熊梦辉,等.高校物质采购过程中索赔谈判分析[J].中国医学装备,2011,8(2):26-28.

[8]曹炳元.应用模糊数学与系统[M].北京:科学出版社,2005:34-91.

[9]谢季坚,刘承平.模糊数学方法及其应用[M].武汉:华中理工大学出版社,2000.

[10]陈贻源.模糊数学[M].武汉:华中工学院出版社,1984:243-276.

[11]彭伟,谢志发,朱海波,等.网上竞价在高校设备采购中的实践和思考[J].实验室研究与探索,2012,31(11):186-188.

[12]师秀清.高校政府采购制度的应用及完善[J].实验技术与管理,2012,29(12):221-224.

[13]付沙,宋丹.基于AHP和模糊综合评判的信息安全风险评估方法[J].实验室研究与探索,2012,31(6):207-210.

[14]李志伟,宋守信,赵志龙.基于模糊综合评判法的信息安全风险评估方法与模型研究[J].生产力研究,2009(19):71-72.

[15]刘鹏超,张喜刚.AHP-模糊综合评价法在高校科研实验室评估中的应用[J].中国电力教育上,2011(4):134-135.

[16]肖光进,刘建秋.多因素决策的模糊评价模型[J].统计与决策,2007(9):12-14.