基于FLS-SVM的火花塞离子电流点火信号时间差软测量模型及其应用
邓清方,袁文华
(邵阳学院 机械与能源工程系,湖南 邵阳,422004)
在火花点燃式发动机中利用其自身的火花塞作为传感器,在火花塞2个电极间外加1个适当的偏置电压,当发动机燃烧室内混合气燃烧时,燃气被离子化,使火花塞间隙的带电离子在外加电场的作用下发生定向流动,形成火花塞离子电流[1-3]。但是,由于发动机进气歧管形状、气缸进气正时误差、大气状况以及传感器精度等因素的影响,使离子电流的出现和点火信号存在偏差,对其精度的控制产生一定的影响,并且在其进气道、燃烧室内高度湍流与脉动气流及脉动燃油之间的热量、质量及动量的传递过程十分复杂[4-6],因此,很难通过机理分析用准确的数学模型来描述其控制变量与缸内混合气燃烧之间的关系,而火花塞离子电流点火信号时间差包含有大量的发动机燃烧和运转信息[7-8],通过对其特征参数进行智能优化控制可以有效地提高燃油利用率和降低其排气污染物。目前,在研究火花塞离子电流点火信号控制方面取得了一些成果[9-10]。文献[9]提出了一种基于试验统计模型的电控汽油机点火提前角多目标优化方法,对最佳点火提前角进行标定;文献[10]采用糊神经网络的理论方法,以点火提前角度、发动机的功率和转速等特征参数作为二次变量,提出了点火提前角时间差软测量模型。在上述研究中,所采用的方法都是基于对火花塞离子电流点火信号进行智能优化控制,由于所建立的模型存在决策变量制约矛盾或者对其样本的数量要求较大,致使在线实现较困难。为此,本文作者在文献[10]的基础上采用模糊最小二乘支持向量机(fuzzy least squares support vector machines, FLS-SVM)对火花塞离子电流点火信号时间差进行有效控制[11-13],并采用混沌量子遗传算法对模糊最小二乘支持向量机的参数进行优化,建立基于FLS-SVM的火花塞离子电流点火信号时间差软测量模型,以便为火花塞离子电流点火信号的有效控制提供技术支持。
1 基于FLS-SVM的火花塞离子电流点火信号时间差软测量模型构建
1.1 火花塞离子电流点火信号时间差软测量原理
发动机进气道喷射混合气的形成是一个非常复杂的过程,其操作变量主要是发动机转速、负荷(节气门开度)和喷油脉宽等,还涉及进气道、燃烧室里高度湍流与脉动气流及脉动燃油之间的热量、质量及动量的传递过程。点火时刻对车用发动机工作的影响很大。从火花出现到混合气大部分燃烧完毕而使汽缸内压力上升到最高值需要一定时间,虽然这段时间较短,但发动机转速很高,在这短时间内,曲轴可转过一定角度。若恰好在活塞到达上止点时点火,则混合气一面燃烧,活塞一面下移而使汽缸容积增大,这将导致燃烧压力降低,发动机的功率也随之减少。影响火花塞离子电流点火信号时间差的因素较多,最主要的因素是发动机的转速、转矩、点火提前角和混合气的燃烧速度,而混合气的燃烧速度又与混合气的成分、发动机的结构及其他因素有关,因此,很难通过机理分析用准确的数学模型来描述这些操作变量与缸内混合气燃烧之间的关系。针对火花塞离子电流特性的研究表明:火花塞离子电流一方面能表征发动机转速、转矩及点火提前角等操作变量的变化状况;另一方面与点火提前角时间差有密切关系。为此,提出基于模糊最小二乘支持向量机的火花塞离子电流点火信号时间差软测量模型,估计点火信号时间差。
基于 FLS-SVM的火花塞离子电流点火信号时间差软测量模型的基本思想是:以点火提前角度θ、发动机的扭矩Tq和转速n作为模型输入的特征参数,并用模糊最小二乘支持向量机表征火花塞离子电流信号到点火信号时间差Δτ的映射关系。根据样本中θ,Tq和n之间的关系和点火信号时间差Δτ对模糊最小二乘支持向量机网络软测量模型进行离线训练;最后将训练好的软测量模型应用于在线测量。
1.2 模糊最小二乘支持向量机
火花塞离子电流点火信号时间差软测量模型样本可以表述为:
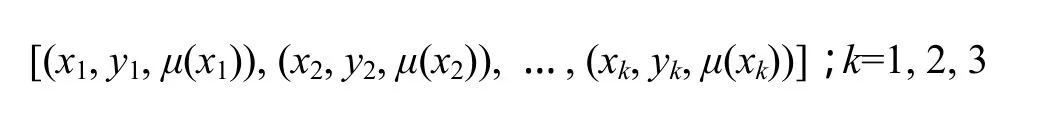
其中:xk表示模型输入特征参数,如点火提前角度θ、发动机的扭矩Tq和转速n;yk表示模型输出特征参数即 Δτ;μ(xk)为隶属度函数,0<μ(xk)≤1。
μ(xk)表示火花塞离子电流点火信号特征参数模糊化后的模糊预选规则,表征样本属于某个类别的程度,并作为火花塞离子电流点火信号时间差软测量模型,在训练样本时,表明每个样本对于其学习所产生权重的影响。通过模糊隶属度,模糊最小二乘支持向量机的最优分类面为下列目标函数的最优解:
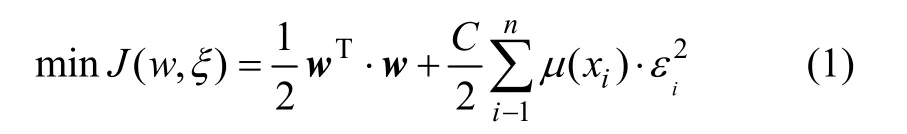
式中:εi=wT·φ(xi)+b-yi, 且εi>0;b为阈值。其拉格朗日函数可表示为

则利用模糊最小二乘支持向量机所要优化的问题可转换为对线性方程的求解问题:
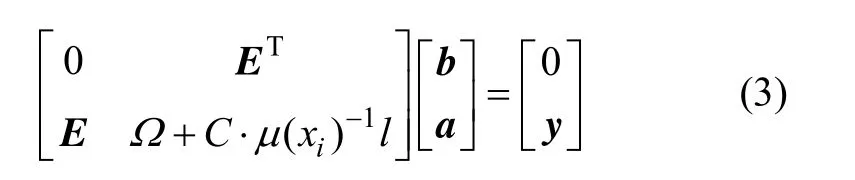
式中:E=[1,1,…,l]T;y=[y1,y2,…,yn]T;a=[a1,a2,…,an]T;Ωij=K(xi,xj) =φ(xi)·φ(xj)。则基于模糊最小二乘支持向量机的火花塞离子电流点火信号时间差软测量模型为
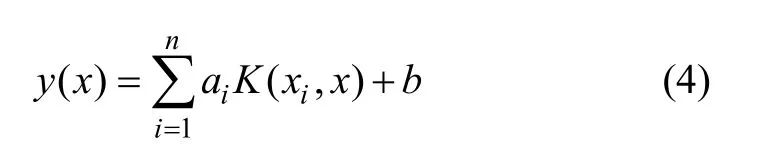
式中:K(xi,x)为核函数即φ(xi),当其满足Mercer条件时,对称的核函数φ(xi)与特征空间点积对应。
基于模糊最小二乘支持向量机的火花塞离子电流点火信号特征参数网络拓扑结构如图1所示,其软测量模型建立和训练过程中对核参数σ和惩罚参数C的有效确定是关键因素。
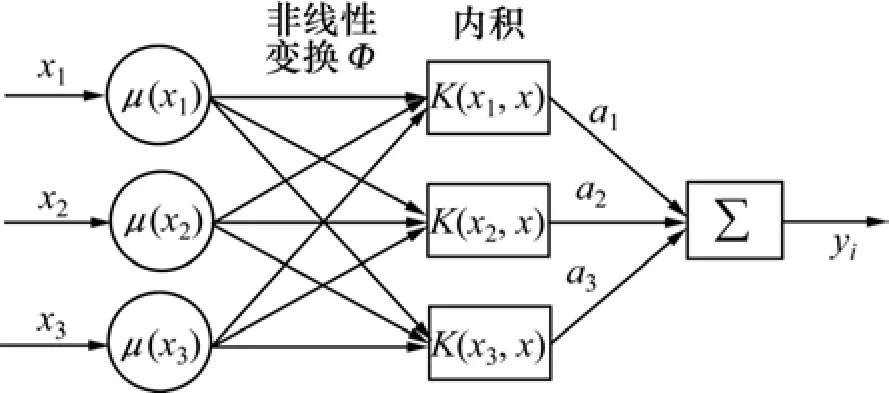
图1 基于FLS-SVM的点火信号时间差软模型网络拓扑结构Fig.1 Network topology on soft-measuring model based on FLS-SVM
1.3 基于混沌量子遗传算法的FLS-SVM参数优化
在标准 FLS-SVM 中,影响模型性能的主要参数有容许误差e、惩罚因子C以及核函数参数σ。参数e表征系统对估计函数在样本数据上误差的期望,使支持向量机的解具有稀疏性,增强泛化能力;惩罚因子C的作用是在确定的数据子空间中调节FLS-SVM这个学习机器的置信范围和经验风险的比例,使其推广性能最好;核函数的参数σ反映了训练数据的特性,对于系统的泛化能力影响较大。本文选用混沌量子遗传算法对FLS-SVM参数进行优化[14-15]。由于实现混沌量子遗传算法的首要任务是在于选择其适应度函数,所选择的适应度函数为
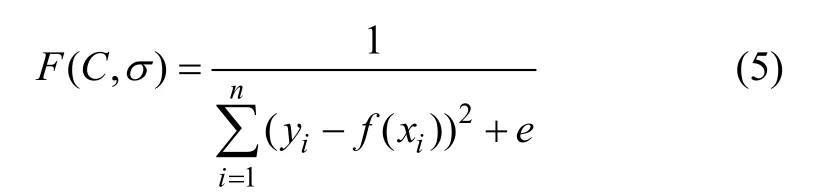
式中:f(xi)为实际输出;yi为期望输出;e=10-3,其作用是使分母不为0。
混沌量子遗传算法基本思想是把混沌变量线性映射到优化变量的取值区间,然后利用混沌变量进行搜索,而且混沌算法对于初值有较强敏感性。该算法弥补了遗传算法在进行寻优时容易陷入局部极值点的缺陷。其算法程序分为2部分,即粗搜索部分和细搜索部分。
1.3.1 粗搜索
Step 1混沌变量的初始值。若r维空间中的点或向量设定为r维连续空间的优化问题,则连续的优化问题可表达如下:

式中:ai≤Xi≤di;i=1, 2, …,r;r为优化的变量个数;[ai,di]为变量Xi的取值范围。
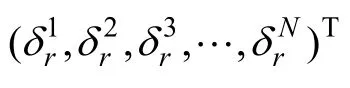
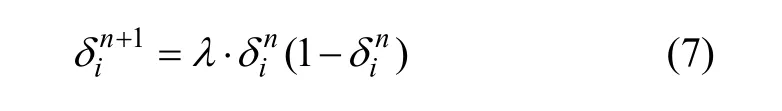
式中:λ=4。
Step 2量子比特编码。利用r组混沌变量先将遗传算法的染色体进行初始化种群,以第j个染色体初始化为例,其结果为

式中:αi= c os(2π );βi= s in(2π )。
采用实数位对算法进行编码,用量子比特构成染色体,并将其概率幅度作为基因位,所以,每条染色体包含上、下2条并列的基因链。由于量子位编码对解空间的遍历性进行了补充和扩展,这将加快搜索进程,使解得全局最优的概率得到很大提高。为了种群结构的多样性,本文采用混沌变量对种群进行初始化。
Step 3构造观测态。依据P(t)中各个体概率幅度产生一组预备解Q(t),Q(t)= {b1,b2, …,br}(其中,br为每个体的观测状态)。在[0,1]范围内任意产生ps,ps>|aj|2,则的第j位取βj,否则取aj(其中,j=1, 2,3, …,r)。
Step 4解向量的线性变换。由于量子遗传算法种群中的每条染色体都含个数为2r的量子比特的概率,采用线性变换将具有遍历空间特征的量子比特的概率变换成优化函数问题的解向量的确定。量子遗传算法种群中的染色体概率分别与解向量的相应优化变量对应。
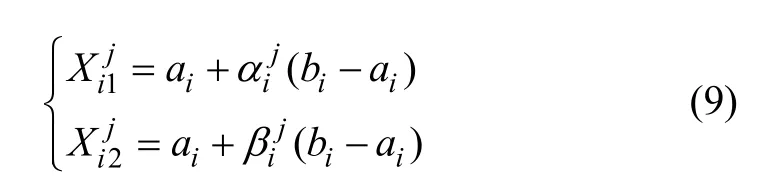
其中:i=1, 2, …,r。由式(12)可知:量子遗传算法种群中的染色体与优化函数问题的2个解对应,从而确保了对空间遍历性的扩展。其预备解Q(t)按式(9)进行线性变换得到解向量中的不同变量值,以目标函数为适应度函数对种群中所有个体的适应值进行评价,记录当前的最优解P0′并与当前的目标值P0进行比较:若 fit(P0′)>fit(P0),则P0=P0′,即以新的最优解作为下一次迭代的目标值,并进行量子位更新;否则,保持当前的目标值不变。
Step 5程序终止判定。若算法符合其终止要求,则程序运行结束,并保存当前解X;否则,算法程序继续运行。
1.3.2 细搜索
若算法经过粗搜索多次迭代后,当前的目标值P0能保持固定不变,则程序运行进入细搜索的阶段。序列Zi的确定是根据Z0的初始赋值决定,其中向量的各个元素按照式(10)构造混沌序列。
Step 1产生搜索变量:
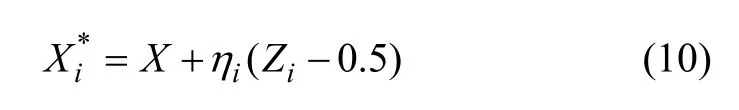
式中:ηi为系数,根据实际情况而定。X在其两侧的邻域范围内进行变量搜索,使得式(10)中ηi(Zi-0.5)为小幅度混沌变量。
Step 2根据目标函数评价其,判断f():若f()>f(X),则f(X) =f();否则,继续搜索。
Step 3程序终止判定:若算法符合其终止要求,则输出解X,并结束其搜索;否则,算法程序继续运行Step 1。
1.4 火花塞离子电流点火信号时间差软测量模型参数的确定
影响其火花塞离子电流点火信号时间差的因素参数很多,其中点火的提前角度、发动机的扭矩和转速影响最大。本文通过结合 FLS-SVM网络的特点,以火花塞离子电流点火信号时间差作为软测量对象,确定其输入变量参数为点火提前角度、发动机功率和转速,输出变量参数为火花塞离子电流点火信号时间差Δτ(即离子电流信号在点火信号出现时的时间间隔)。其火花塞离子电流点火信号特征参数样本集如表1所示。
选取表1中的前30组数据作为火花塞离子电流点火信号时间差软测量模型训练样本数据,并采用模糊最小二乘支持向量机对其样本数据进行训练,利用后10组数据考查火花塞离子电流点火信号时间差软测量模型的泛化能力。
2 基于FLS-SVM的火花塞离子电流点火信号时间差软测量模型应用
2.1 火花塞离子电流点火信号时间差软测量模型分析与验证
根据火花塞离子电流点火信号特征参数的特点,以火花塞离子电流点火信号时间差作为软测量对象,并以表1中的点火提前角、发动机的扭矩和转速作为模糊最小二乘支持向量机的输入参数,经过500次训练后,以表1中的后10组数据作为测试样本集,并用火花塞离子电流点火信号时间差软测量模型来仿真网络的输出,从而与实际输出进行比较,检验其火花塞离子电流点火信号时间差软测量模型的性能。其模型输出值与实际值的对比和误差分别如图2和图3所示。

表1 NGK BP7HS型火花塞离子电流点火信号特征参数样本集Table 1 Sample set of characteristic parameters of NGK BP7HS
从图2和图3可以看出:模型输出值和实际值都很接近,说明基于模糊最小二乘支持向量机,以点火提前角、发动机的扭矩和转速为特征参数的火花塞离子电流点火信号时间差软测量模型是有效的,其火花塞离子电流点火信号时间差软测量模型精度的相对误差小于1%,说明精度较高。

图2 火花塞离子电流点火信号时间差Δτ软测量对比图Fig.2 Comparison chart of soft-measuring model output
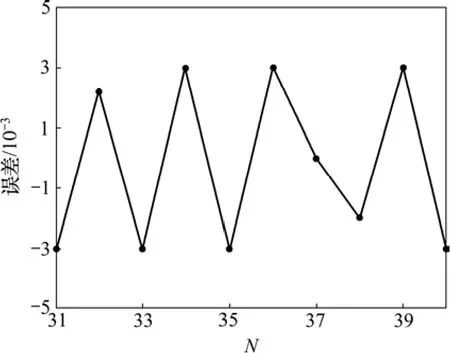
图3 火花塞离子电流点火信号时间差软测量误差Fig.3 Relative error of time difference of soft-measuring model
2.2 火花塞离子电流点火信号时间差软测量模型在线应用效果
图4所示为火花塞离子电流点火信号时间差软测量模型在线应用示意图。将所建立的软测量模型嵌入PC机系统中,从而使系统能够实时根据发动机的转速、扭矩和点火提前角对花塞离子电流点火信号进行优化控制。试验发动机采用ZS156MI单缸水冷汽油机,其排量为 124.04 mL,最大功率转速为 8 500 r/min,最大扭矩为9.2 N·m,标定功率为8.5 kW。对试验工况为冷启动,进气压力pd=60 kPa,转速n=1 600 r/min和点火提前角为17°时的发动机连续运行70 h的排放性能进行研究,并与未控制前的原型发动机性能进行对比。其发动机排放性能如表2所示。
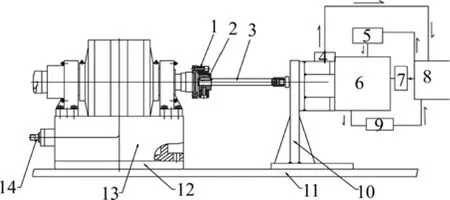
图4 火花塞离子电流点火信号时间差模型在线应用示意图Fig.4 Schematic of online application about soft-measuring model

表2 排放性能对比Table 2 Comparison of emission behavior
从表2可知:将火花塞离子电流点火信号时间差软测量模型应用于ZS156MI单缸水冷汽油机后,其花塞离子电流点火信号得到了有效控制,并且该软测量模型能在连续工作70 h内实现了点火。其主要原因是火花塞离子电流点火信号时间差软测量模型对点火信号和离子电流信号出现的时间差进行了有效估算,因此,能更好地保障发动机内燃烧情况的优化,其优化控制后的发动机 CO体积分数比原型发动机降低8.61%;NOx体积分数降低12.83%;HC体积分数降低7.68%,取得了较好的排放性能。
3 结论
(1) 根据模糊最小二乘支持向量机的理论方法,提出了一种基于发动机的转矩、转速以及点火提前角为特征参数的火花塞离子电流点火信号时间差软测量模型,并采用混沌量子遗传算法对模糊最小二乘支持向量机的惩罚函数C和核参数σ进行了优化。该软测量模型所得参数相对误差小于1%,具有较高的精度。
(2) 基于 FLS-SVM 的火花塞离子电流点火信号时间差软测量模型对其发动机排放控制效果较好,其优化控制后的发动机CO体积分数与原型发动机的相比降低8.61%,NOx体积分数降低12.83%,HC体积分数降低7.68%,取得了较好的排放性能。
[1] 李建文, 刘书亮, 王崇. 基于虚拟仪器的火花塞离子电流采集与分析系统的研究[J]. 计量学报, 2005, 20(3): 218-231.
LI Jianwen, LIU Shuliang, WANG Chong. A study of spark plug ion current signal acquisition and analytic system based on virtual instrument[J]. Acta Metrologica Sinica, 2005, 20(3):218-231.
[2] ZHU Guoming, David L S, Jim W. Combustion characteristics detection for low pressure direct injection engines using ionization signal[J]. SAE Paper, 2006-01-3317.
[3] Shimasaki Y, Maki H, Sakaguchi J. Study on combustion monitoring system for formula one engines using ionic current measurement[J]. SAE Paper, 2004: 2004-01-1921.
[4] Kubach H, Amin V, Spicher U. Ion current measurement in diesel engines[J]. SAE Paper, 2004: 2004-01-2922.
[5] Gregory B J, Chen J Y, Dibble R W. The effects of intake pressure fuel concentration and bias voltage on the detection of ions in a homogeneous charge compression ignition engine[J].Proceedings of the Combustion Institute, 2009, 32(2):2877-2884.
[6] GAO Zhongquan, WU Xiaomin. The relationship between ion current and temperature at the electrode gap[J]. Applied Thermal Engineering, 2012, 33(34): 15-23.
[7] Rivara N, Dickinson P B, Shenton A T. A transient virtual-AFR sensor using the in-cylinder ion current signal[J]. Mechanical Systems and Signal Processing, 2009, 23(5): 1672-1682.
[8] 成志明. 基于模糊神经网络的火花塞离子电流的软测量理论方法及应用[D]. 长沙: 湖南大学机械与汽车工程学院, 2007:37-42.
CHENG Zhiming. Soft-measuring theory and application of spark ion current base on the fuzzy control and neural networks theory[D]. Changsha: Hunan University. Mechanical and Vehicle Engineering, 2007: 37-42.
[9] 吴锋, 贾岱润, 姚拣伟, 等. 电控汽油机点火提前角多目标优化方法研究[J]. 内燃机工程, 2008, 29(1): 24-28.
WU Feng, JIA Dairun, YAO Dongwei, et al. Research on multi-objective optimization of spark advanced angle for efi gasoline engine[J]. Chinese Internal Combustion Engine Engineering, 2008, 29(1): 24-28.
[10] 谢常清, 鄂加强, 成志明, 等. 基于模糊神经网络的点火提前角时间差软测量模型[J]. 内燃机工程, 2009, 30(2): 73-77.
XIE Changqing, E Jiaqiang, CHENG Zhiming, et al.Soft-measuring model of timing difference about pre-ignition angle base on the fuzzy control and neural networks theory[J].Chinese Internal Combustion Engine Engineering, 2009, 30(2):73-77.
[11] Lamorski K, Pachepsky Y, Slawinski C. Using support vector machines to develop pedotransfer functions for water retention of soils in Poland[J]. Soil Sci Soci Am J, 2008, 72(5):1243-1247.
[12] Bouhouche S, Yazid L L, Hocine S, et al. Evaluation using online support-vector-machines and fuzzy reasoning: Application to condition monitoring of speeds rolling process[J]. Control Engineering Practice, 2010, 18(9): 1060-1068.
[13] Vong C M, Wong P K. Engine ignition signal diagnosis with wavelet packet transform and multi-class least squares support vector machines[J]. Expert Systems with Applications, 2011,38(7): 8563-8570.
[14] Sengur A. Multiclass least-squares support vector machines for analog modulation classification[J]. Expert Systems with Applications, 2009, 36(3): 6681-6685.
[15] Juang C F, Hsieh C D. TS-fuzzy system-based support vector regression[J]. Fuzzy Sets and Systems, 2009, 160(17):2486-2504.

