航空渐开线花键副微动摩擦接触参数分析

胡正根，朱如鹏，靳广虎，倪德

(南京航空航天大学 江苏省精密与微细制造技术重点实验室, 江苏 南京，210016)

与普通平键相比，渐开线花键副以其受力均匀、承载能力大以及对中性和导向性好等优点，在航空机械传动中运用广泛[1]。据美国西南研究院(SwRI)调查，超过174个各类花键联接运用于美国海军单发动机黑鹰攻击机(A-4)上，超过200个花键联接运用于多发动机飞机上[2]。但是，由于航空渐开线花键的工况恶劣，而且是薄壁结构，接触齿面易发生微动摩擦，使得花键接触齿面磨损严重，导致联接失效，这类故障在型号研制和现役机型中已发生多起[1]。为提高花键联接质量，国内外学者就花键副的设计理论和方法开展了一系列研究工作。Leen等[3-9]采用有限元分析方法对扭矩过载情况下的螺旋花键副的疲劳寿命预测进行了研究，结果表明花键联轴器与单一拉伸疲劳试验之间具有良好的关联性。Ku等[10-11]研究了润滑、材料和花键轴偏置对花键磨损的影响，对可以降低花键轮齿磨损的设计与润滑参数进行了研究；Ding等[12-17]采用有限元方法对花键副微动磨损进行了仿真分析，并将预测结果与疲劳试验结果进行了对比 Medina等[18-19]采用弹性静力学接触模型对偏心传动轴传动系统花键的应力分布进行了研究。国内对花键联接的强度、磨损、刚度等也作了一定的研究和试验，如陈卓等[20]对航空发动机渐开线花键强度进行了分析；韩晓娟[21]研究了轴毂不同轴度所引起的微振磨损对挠性花键联接寿命的影响，并将此定量地引入花键联接的强度计算中，给出了低同心精度花键联接的强度计算方法。本文作者针对典型的航空渐开线花键联接形式，采用有限元方法，获得航空渐开线花键副的接触应力及相对滑移分布规律，并研究接触长度、花键壁厚及摩擦因素对渐开线花键副微动摩擦接触的影响，以便为航空渐开线花键副的设计及工程运用提供参考。

1 渐开线花键副有限元模型

1.1 花键副几何模型

花键副的精确建模对微动摩擦接触分析的准确性至关重要。本文使用的模型是基于VB.net对CATIA二次开发得到，齿面精度能满足分析要求，齿廓参数参照GB/T 3478.1—2008。图1所示为典型的圆齿根花键副几何模型[1]，内花键为主动轴，外花键为从动轴，外花键和内花键的齿侧间隙为0；x方向沿外花键接触面，z方向为花键副的轴向方向。模型计算参数及材料属性如表1所示。图1中：Db为外花键内孔直径；Do为内花键轴径；D为分度圆直径；a1为轴向接触长度；a2为径向接触宽度；T为施加扭矩。

表1 渐开线花键副模型参数Table 1 Parameters of involute spline couplings

图1 典型花键副几何模型Fig.1 Geometry model of typical spline couplings

1.2 花键副有限元模型

将 CATIA 中的几何模型导入 ANSYS workbench13.0，实现无缝连接，获得有限元分析几何模型。由于摩擦接触分析属非线性问题，需消耗大量的计算资源，为节省计算资源，提高计算精度，取 1对齿啮合进行分析，用循环对称边界条件得到花键副全齿应力图。网格密度对有限元分析结果精度的影响较大，需对其进行试算。首先，采用一定的网格密度进行计算，而后在接触区域细化网格。多次试算后，若计算结果差异很小，则表明计算结果收敛。图2所示为经过网格试算的花键副有限元模型。从图2可见：当单元总数为44 300，节点总数为202 548时，计算结果趋于收敛。

图2 花键副有限元模型Fig.2 Finite element model of typical spline couplings

1.3 边界条件与接触设置

1.3.1 边界条件

采用循环对称条件，模拟花键副全齿模型，外花键输出轴的B面固定。扭矩等效为一系列沿着内花键输入轴A面顶端弧线的切向节点力；同时保证A面扭矩施加位置与接触区域距离足够远，使扭矩的施加方式不影响接触分析[4]。

1.3.2 接触设置

花键副的接触属于弹性体之间的面-面接触问题。接触面和目标面选取很重要，若选择不当会引起穿透量过大，影响求解精度。在一般情况下，当凸面和平面或凹面接触时，应指定凹面或平面为目标面，因此，花键副的内花键齿面设定为目标面。2个接触表面之间穿透量取决于法向接触刚度，需要确定接触物体的法向接触刚度。若法向接触刚度过大，则会增加求解的收敛次数，可能导致结果不收敛；若法向接触刚度过小，则接触面之间的节点穿透量过大，造成接触模型不稳定，导致分析结果错误。基于以上因素，本文先使用小的法向接触刚度系数，而后逐步增大法向接触刚度系数，直到前、后2次的分析结果相差很小为止，从而确定最佳法向接触刚度系数。经过0.001, 0.01,0.1, 1.0, 1.1共 5种法向接触刚度系数的计算结果比较，当法向接触刚度系数为1.0时可以得到较好结果。非线性摩擦接触问题的算法主要有增广拉格朗日法和罚函数法，经计算比较发现：这2种方法的计算结果几乎相同。综合考虑计算时间及精度，本文采用增广拉格朗日法对花键副非线性摩擦接触进行分析。

经求解，花键副的接触应力和相对滑移有限元结果云图如图3所示。最大接触应力和最大相对滑移在轴向z=a1处。

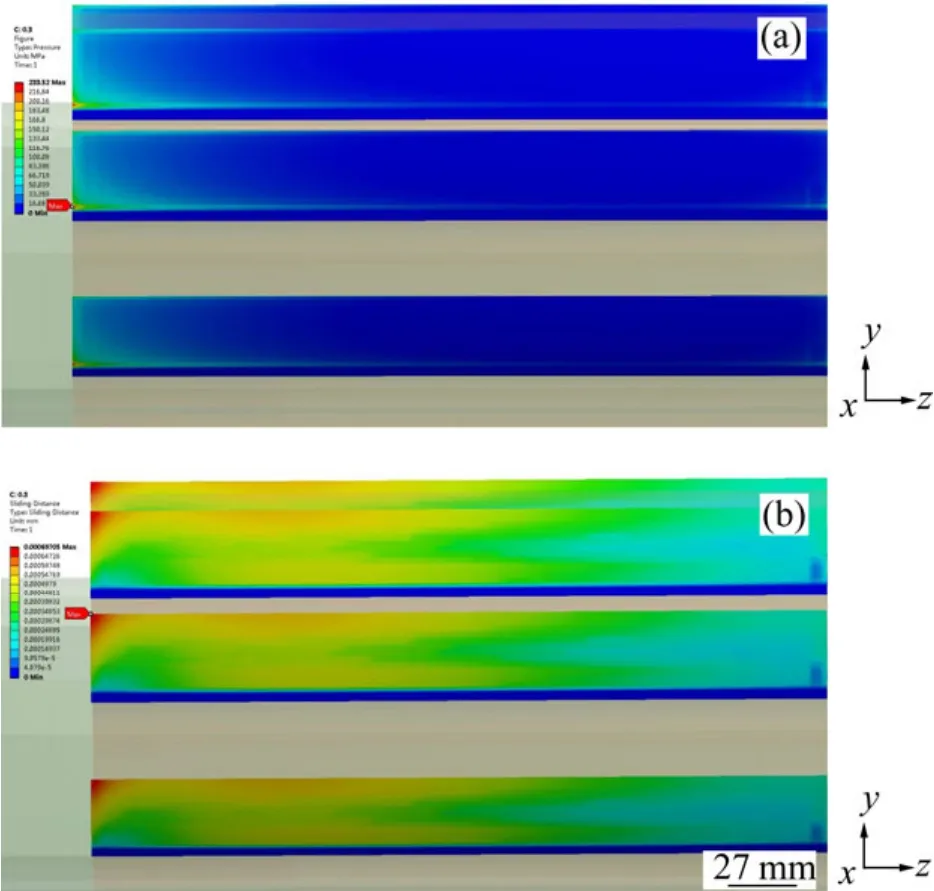
图3 花键副接触应力和相对滑移分布云图Fig.3 Contact pressure and relative slip maps of spline couplings

2 计算结果与分析

为考察接触应力和相对滑移分布规律及其影响因数，对接触应力p、相对滑移δ、轴向接触位置z、径向接触位置x、接触长度a1、外花键内孔直径Db进行无量纲处理。其中接触应力相对于平均接触应力pc，相对滑移和径向接触位置相对于径向接触宽度a2，轴向接触位置相对于轴向接触长度a1，接触长度和外花键内孔直径相对于分度圆直径D。pc=15.838 MPa，a2=2.887 mm。

2.1 接触应力及相对滑移分布

花键副接触应力和相对滑移分布见图4。从图4(a)和图4(b)可知：花键副接触应力分布不均匀。图4(a)表明：从外花键接触面齿顶开始接触应力先减小后增大，在接触面径向顶端和底端有应力集中，且x=a2处比x=0处更大，这与2个位置存在几何突变而产生应力集中的现象相符合。图4(b)表明：接触应力沿轴向方向也是先减小后增大，在轴向接触开始和结束处有应力集中，且z=a1处比z=0处更大。这是由于z=0的位置是内花键扭矩输出最大位置，z=a1的位置是外花键输入扭矩最大位置，且这2个位置也存在几何突变，易产生应力集中。结合齿面轴向和径向接触应力分布规律，可知最大接触应力出现在接触面的x=a2和z=a1附近。

由图3(c)和图(d)可知：相对滑移从外花键接触面齿顶沿着径向方向有减少的趋势，但是改变量较小；轴向的相对滑移沿着轴向则有增大的趋势，且增大趋势明显。结合齿面轴向和径向相对滑移分布规律，可知最大相对滑移发生在接触面的x=0和z=a1附近。

综合花键副的接触应力和相对滑移分布规律可知：轴向z=a1处是花键副的危险位置，在该处接触应力和相对滑移均达到最大，这与花键副实际使用中该位置经常发生微动失效相符合。

2.2 接触长度的影响

由花键平均接触应力计算方程可知[4]：平均接触应力随花键副接触长度的增大而减少，增加接触长度能够增大承载能力。但是，随着接触长度的增加，最大接触应力并没有随之减少。这是因为接触长度增加导致花键副接触齿面载荷不均匀系数增大，而且无量纲接触应力曲线变得更加陡峭，轴向载荷不均匀程度变大，特别是在z=a1附近，如图5(a)和图5(b)所示(其中，Pmax和δmax分别为最大接触应力和最大相对滑移)。从图5(a)和图5(c)可以看出：花键副接触长度的增加可以减少最大相对滑移，当接触长度超过一定值时，最大相对滑移相对稳定，减少趋势不明显。

图4 花键副接触应力和相对滑移分布Fig.4 Contact pressure and relative slip distributions of spline couplings

综合花键副接触长度对接触应力和相对滑移的影响，对于纯扭矩传递，当接触长度与花键副分度圆直径之比为1/2时是最佳的；当超过1/2时，最大接触应力和最大相对滑移几乎不受接触长度的影响，增大接触长度已经不能起到增大承载能力和减少相对滑移的作用：因此，在保证花键副联接工作能力的条件下，花键副接触长度应该尽可能地取较小值。花键副接触长度过长会导致花键副的载荷不均匀程度增加，工程上，一般不采用a1/D＞1.2的花键联接[1]。

2.3 花键壁厚的影响

花键壁厚也是影响花键副接触应力和相对滑移分布的一个重要因素，本文以外花键壁厚为例。由图6(a)和图6(b)可知：外花键壁厚对接触应力分布会产生影响；在外花键内孔直径和花键副分度圆直径之比超过1/2时，花键副最大接触应力随外花键内孔直径的增加而增大，导致花键副承载能力下降；接触应力较小的区域对外花键壁厚不敏感，在轴向z＜0.8a1区域时，接触应力几乎不受壁厚影响；在轴向z＞0.8a1区域时，接触应力随外花键壁厚减少而增加，如图6(b)所示。图 6(a)可知：当外花键内孔直径和花键副分度圆直径之比超过1/2时，花键副的最大相对滑移随外花键的内孔直径增大而增大；在轴向z＜0.5a1区域时，外花键的壁厚对相对滑移几乎不产生影响；在轴向z＞0.5a1区域时，壁厚越薄，相对滑移越大，与壁厚对接触应力影响类似，如图6(c)所示。

综合考虑外花键壁厚对接触应力和相对滑移的影响，在外花键内孔直径与花键副分度圆直径之比小于1/2时，外花键壁厚对接触应力及相对滑移几乎没有影响；超过1/2时，主要影响接触面端部的接触应力及相对滑移，但是，对接触应力和相对滑移较小的接触面中部几乎没有影响：因此，在花键副设计时，常将外花键设计成端面壁厚、中间壁薄的结构，而内花键也常设计成变截面的结构，这可以有效保证渐开线花键副的载荷沿齿长均匀分布，同时，在航空减小质量方面也具有很重要的现实意义[1]。

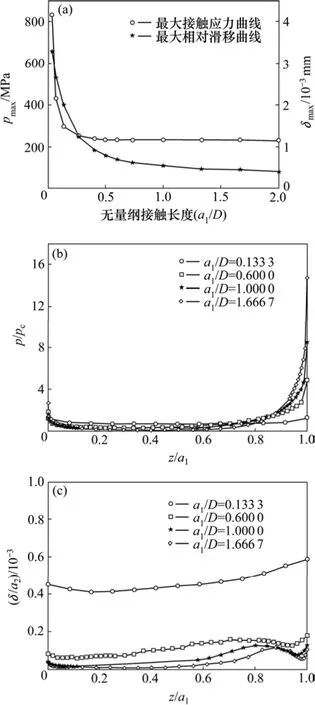
图5 接触长度对接触应力和相对滑移的影响Fig.5 Effect of contact length on contact pressure and relative slip

2.4 摩擦因素的影响

图6 外花键内孔直径对接触应力和相对滑移的影响Fig.6 Effects of bore diameter of external spline on contact pressure and relative slip

图7所示为摩擦因素对接触应力和相对滑移的影响。从图 7(a)和图7(b)可以看出：花键副的最大接触应力随摩擦因素增加有减少趋势，但改变量很小，故花键齿的光滑程度，对花键副的承载能力几乎没有影响。从图 7(a)和图 7(c)可见：摩擦因素对花键副的相对滑移影响较大，摩擦因素越大，相对滑移越小；当摩擦因素μ=0.5时，接触面存在滑移区，黏着区和部分滑移区3种状态；当μ=0.7时，花键副接触面几乎完全处于黏着状态。微动图理论指出：微动疲劳寿命的降低比例主要取决于局部疲劳的强烈程度，出现的短寿命凹区是局部疲劳最强烈的区域，从微动区域分布来看，基本处于微动混合区域，工程上为减缓花键副微动损伤，经常通过润滑的方式来减少花键副接触区域的摩擦因素。而微动破坏的缓减程度主要取决于润滑介质在接触表面处的耐久性[22-23]。

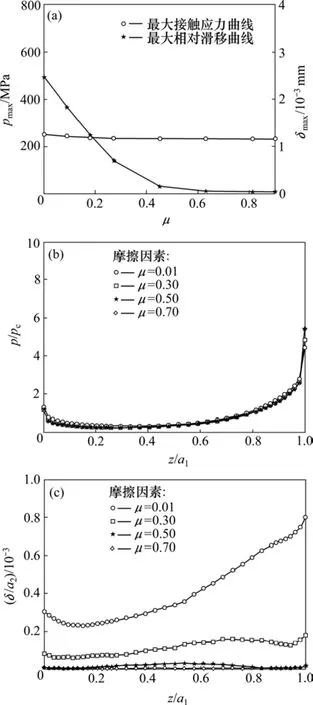
图7 摩擦因素对接触应力和相对滑移的影响Fig.7 Effect of friction coefficient on contact pressure and relative slip

3 结论

(1) 外花键靠近输出轴的端面接触应力和相对滑移达到最大值，微动磨损严重，因此，齿向修形将会改善花键副接触应力和相对滑移的端面集中现象。

(2) 花键副接触长度对花键副接触应力和相对滑移的影响较大，在保证强度的条件下，应尽量取较小的接触长度，使得a1/D＜1.2。

(3) 花键壁厚会影响花键副接触特性，壁厚越小，端面接触应力及相对滑移增大，但对接触齿面的中部影响较小。

(4) 接触区域摩擦因素对接触应力没有影响，但对相对滑移影响较大。

[1] 布尔加科林夫. 航空齿轮传动和减速器手册[M]. 常春江, 等,译. 北京: 航空工业出版社, 1988: 199-203.

Colin B L. Aviation gear drive and reducer manual[M]. CHANG Chunjiang, et al, trans. Beijing: Aviation Industry Press, 1988:199-203.

[2] Kececiogulu D, Koharcheck A. Reliability of aircraft splines with or without a wear induction period[J]. Journal of Vibration,Acoustics, Stress and Reliability in Design, 1983, 105(2):163-170.

[3] Leen S B, Mccoll I R, Ratsimba C H H, et al. Fatigue life prediction for a barrelled spline coupling under torque overload[J]. Journal of Aerospace Engineering, 2003, 217(3):123-142.

[4] Leen S B, Hyde T R, Williams E J, et al. Development of a representative test specimen for frictional contact in spline joint couplings[J]. Journal of Strain Analysis, 2000, 35(6): 521-544.

[5] Leen S B, Richardson I J, Mccoll I R, et al. Macroscopic fretting variables in a splined coupling under combined torque and axial load[J]. Journal of Strain Analysis, 2001, 36(5): 481-497.

[6] Leen S B, Hyde T H, Ratsimba C H H, et al. An investigation of the fatigue and fretting performance of a representative aero-engine splined coupling[J]. Journal of Strain Analysis, 2002,37(6): 565-583.

[7] Madge J J, Leen S B, Shipway P H. A combined wear and crack nucleation-propagation methodology for fretting fatigue prediction[J]. International Journal of Fatigue, 2008, 30(9):1509-1528.

[8] Ratsimba C H H, Mccoll I R, Williams E J, et al. Measurement,analysis and prediction of fretting wear damage in a representative aero-engine spline coupling[J]. Wear, 2004,257(11): 1193-1206.

[9] Hyde T H, Leen S B, Mccoll I R. A simplified fretting test methodology for complex shaft couplings[J]. Fatigue and Fracture of Engineer Materials and Structures, 2005, 28(11):1047-1067.

[10] Ku P M, Valtierra M L. Spline wear-effects of design and lubrication[J]. Journal of Engineering for Industry, 1975, 97(B4):1257-1263.

[11] Valtierra M L, Pakvis A, Ku P M. Spline wear in jet fuel environment[J]. Lubric Eng, 1975, 31(3): 136-142.

[12] Ding J, Mccoll I R, Leen S B. The application of fretting wear modelling to a spline coupling[J]. Wear, 2007, 262(9/10):1205-1216.

[13] Ding J, Leen S B, Williams E J, et al. Finite element simulation of fretting wear-fatigue interaction in spline couplings[J].Tribology-Materials, Surfaces and Interfaces, 2008, 2(1): 10-24.

[14] Mccoll I R, Ding J, Leen S B. Finite element simulation and experimental validation of fretting wear[J]. Wear, 2004,256(11/12): 1114-1127.

[15] Mccoll I R, Waterhouse R B, Harris S J, et al. Lubricated fretting wear of a high-strength eutectoid steel rope wire[J]. Wear, 1995,185(1/2): 203-212.

[16] Wei S S, Williams J W, Leen S B. Finite element, critical-plane,fatigue life prediction of simple and complex contact configurations[J]. International Journal of Fatigue, 2005, 27(4):403-416.

[17] Ding J, Leen S B, Mccoll I R. The effect of slip regime on fretting wear-induced stress evolution[J]. International Journal of Fatigue, 2004, 26(5): 521-531.

[18] Medina S, Olver A V. Regimes of contact in spline couplings[J].Journal of Tribology, 2002, 124(2): 351-357.

[19] Medina S, Olver A V. An analysis of misaligned spline couplings[J]. Journal of Engineering Tribology, 2002, 216(5):269-278.

[20] 陈卓, 朱如鹏. 航空发动机渐开线花键强度分析[J]. 机械工程与自动化, 2009, 155(4): 90-92.

CHEN Zhuo, ZHU Rupeng. Strength analysis of involute spline of aero-engine[J]. Mechanical Engineering and Automation,2009, 155(4): 90-92.

[21] 韩晓娟. 挠性花键联接的强度计[J]. 燕山大学学报, 2001,25(1): 45-46.

HAN Xiaojuan. Strength calculating methods of flexible splines[J]. Journal of Yanshan University, 2001, 25(1): 45-46.

[22] 周仲荣, Vincent L. 微动磨损[M]. 北京: 科学出版社, 2002:140-142.

ZHOU Zhongrong, Vincent L. Fretting wear[M]. Beijing:Science Press, 2002: 140-142.

[23] 周仲荣, 朱旻昊. 复合微动磨损[M]. 上海: 上海交通大学出版社, 2004: 142-144.

ZHOU Zhongrong, ZHOU Wenhao. Compound fretting wear[M].Shanghai: Shanghai Jiaotong University Press, 2004: 142-144.