聚乙烯醇水溶纤维干法纺丝成形模拟

王建铨， 吴津田， 刘鹏清， 叶光斗， 徐建军

(四川大学 高分子材料工程国家重点实验室， 四川 成都 610065)

聚乙烯醇水溶纤维干法纺丝成形模拟

王建铨， 吴津田， 刘鹏清， 叶光斗， 徐建军

(四川大学 高分子材料工程国家重点实验室， 四川 成都 610065)

通过建立顺流式干法纺丝一维模型，加入甬道溶剂平衡方程，结合顺流干燥的工艺特点修正动量平衡方程，对聚乙烯醇(PVA)纺丝线的溶剂含量、温度、速度、张力分布进行计算机模拟，预测了不同纺丝工艺对纺丝过程的影响。结果表明：丝条在闪蒸后处于湿球温度的平衡阶段较长，丝条溶剂含量是控制丝条温度变化的主要因素；在纺丝速度较低的情况下，喷丝头处张力最大；增加甬道风速不利于纺丝速度的提高；增加卷绕速度有利于纤维干燥成形。

聚乙烯醇纤维; 干法纺丝; 纺丝动力学; 计算机模拟

聚乙烯醇(PVA)纤维是合成纤维主要品种之一，早在1924年德国Hermann和Haehnel就将聚醋酸乙烯醇解制得聚乙烯醇，随后又以其水溶液干法纺丝制得纤维。目前聚乙烯醇纤维主要有湿法、干法、凝胶法3种纺丝方法，干法纺丝以其工艺流程短、环保等优异特点而被用来生产聚乙烯醇水溶长丝和其他多功能性或差别化聚乙烯醇纤维[1]。干法纺丝过程较复杂，纺丝原液经喷丝孔挤出后在纺丝甬道中有拉伸流动, 丝条在干燥凝固成形的过程中伴随着传热和传质。Ohzawa等[2-3]曾对聚乙烯醇等几种干纺体系进行模拟，Sano Y[4]基于纺丝工艺对聚乙烯醇干纺体系进行了较准确的数学模拟，并对丝条径向浓度分布进行了研究。但已报道的干法纺丝文献都采用逆流式进行模拟，而顺流式干法纺丝纤维成形较缓和，更有利于生产聚乙烯醇水溶长丝[1]。本文通过建立一维顺流式干法纺丝模型， 从理论上研究了丝条凝固成形过程中速度、浓度、温度、张力的分布规律。

1 干法纺丝动力学模型的建立

1.1 牛顿流体本构方程

(1)

式中，A为纺丝线上丝条截面积，cm2。聚乙烯醇溶液的零切黏度[4]为

(2)

式中：ηw为水的剪切黏度；T为丝条平均温度，K；Pn为聚乙烯醇聚合度；ws为丝条溶剂质量分数。

1.2 质量平衡方程

式(3)表示丝条和气相界面的传输守恒，式(4)表示丝条束与甬道空气的溶剂传输守恒[2]。

(3)

(4)

式中：Wp为聚合物质量流率，g/s；Wa为纺丝甬道内空气质量流率，g/s；n为喷丝头孔数；Ns为丝条表面的溶剂流量，mol/(cm2·s)。

(5)

式中：Ks为溶剂传质系数，mol/(cm2·s)；xss为丝条表面溶剂分压，atm (1 atm=101.325 kPa);xsc为甬道空气中溶剂分压，atm。

(6)

式中P为纯溶剂在空气中的分压，atm。

(7)

活度as可由Flory-Huggins理论[8]得出：

(8)

式中：φs、φp分别为溶剂、聚合物体积分数;Vs、Vp分别为溶剂和聚合物摩尔体积,cm3/mol;χsp为水和聚乙烯醇的相互作用参数,可由下式[9-10]估算:

(9)

1.3 能量平衡方程

(10)

式中：h为传热系数，J/(cm2·s·K)，由努赛尔数Nu=2Rh/ka[2]得出

(11)

式中Rep和Rew分别是基于甬道风速度和丝条速度的雷诺数。

(12)

(13)

式中：Ls为溶剂蒸发潜热，J/mol；Cpp、Cps分别为聚乙烯醇和水的热容，J/g。

1.4 动量平衡方程

(14)

定义体系密度

(15)

式中Cf为阻力系数，N/cm2。

(16)

热风空气的密度ρa、黏度ηa、导热系数ka由下式[6]估算：

ρa=0.351 /Tf

(17)

ηa=1.446×10-6Tf1.5/ (Tf+113.9)

(18)

ka=1.878×10-6Tf0.866

(19)

式中，Tf为薄膜温度，定义为丝条温度和甬道风温度的算术平均数。

干纺动力学的计算机模拟过程如下：使用MatLab数学软件，采用表1、2的纺丝工艺和体系物性参数，代入各个关系式，以方程(1)、(3)、(4)、(10)、(14)建立常微分方程组，编写函数文件，调用MatLab中的非刚性ode45阶函数(Runge-Kutta四五阶函数)求得数值解，计算机模拟过程参数见表1、2。

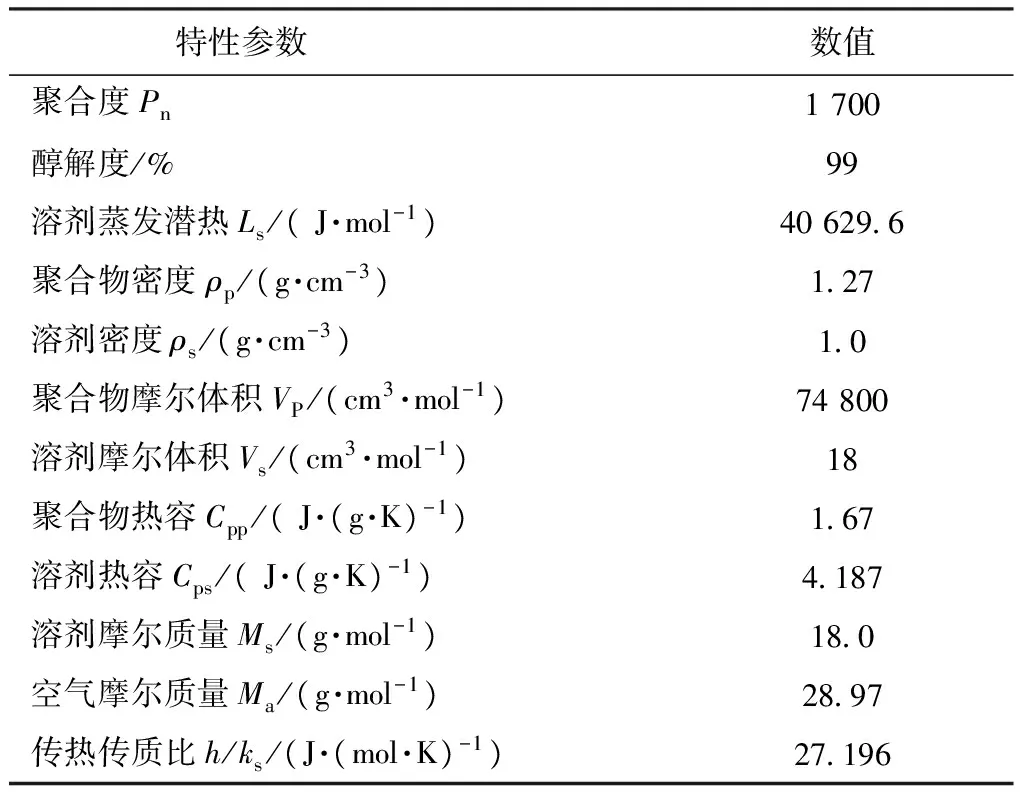
表1 聚乙烯醇/水体系特性参数

表2 纺丝模拟工艺参数

2 结果与讨论

2.1 丝条在纺丝线上的变化

2.1.1 丝条温度和溶剂含量的变化

图1示出丝条温度和溶剂沿纺程的变化。可以看出，随着溶剂的挥发，丝条温度在距离喷丝30 cm左右处就下降到了湿球温度，在这个阶段丝条溶剂的扩散主要靠自身的潜热而使溶剂蒸发，从而使丝条温度迅速下降到湿球温度。由于溶剂水的蒸发潜热大，热风的传热与丝条溶剂的蒸发吸热处于一个较长的平衡阶段，在这个阶段内甬道内水气含量增加，丝条温度缓慢上升。随着丝条溶剂含量的进一步减少，溶剂蒸发速率减慢，丝条温度开始上升，最后升至热风温度。

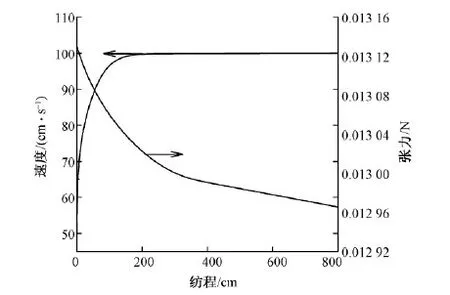
图1 丝条温度和溶剂沿纺程的变化Fig.1 Change of filament temperature and solvent fraction along spinline

2.1.2 丝条速度和张力的变化

图2示出丝条速度和张力随纺程的变化。可见，丝条在拉伸作用下，速度迅速上升到一个平台区间后开始缓慢增加，最后达到卷绕速度。丝条在喷丝头处张力最大。随着丝条速度的增加，丝条与空气的摩擦力也变大，张力随纺程增大而减小，只在纺丝速度较大的情况下，张力才会随纺程增加而变大。由于喷丝头处的丝条黏度最小，因此能承受的张力也最小。初始的张力包括丝条的部分重力和额外的牵伸拉力，所以原液的黏度要在合理的范围内，既能保证原液具有一定的流动性，又能使丝条在喷丝头位置处能承受住较大的张力。

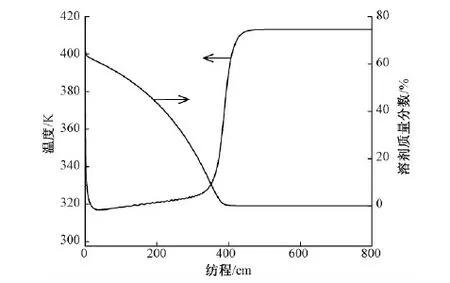
图2 丝条速度和张力随纺程的变化Fig.2 Change of filament velocity and tension along spinline

2.2 纺丝工艺对纺丝过程的影响

2.2.1 泵供量对丝条温度和溶剂含量的影响

图3示出泵供量对溶剂含量分布的影响。可见，随着泵供量的增加，丝条溶剂含量减小趋势变缓。丝条单位时间内吸收热量相同的情况下，溶剂蒸发量也一定，而泵供量增大使丝条的干燥时间增长，从而使丝条在纺程较远处固化。

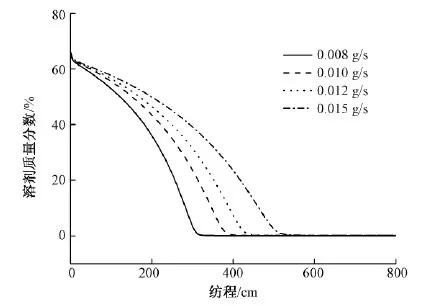
图3 泵供量对溶剂含量分布的影响Fig.3 Effect of mass throughput on solvent content distribution

图4示出泵供量对丝条温度的影响。可见，泵供量的增加对丝条纺程前半部分温度没有太大的影响，都从起始温度降至湿球温度，但保持在湿球温度的纺程变长。对照图3，在丝条溶剂含量减小至平台值时，丝条温度才开始上升至热风温度，由此可见，在丝条降温至湿球温度后，丝条内溶剂的含量是控制其温度变化的关键因素。

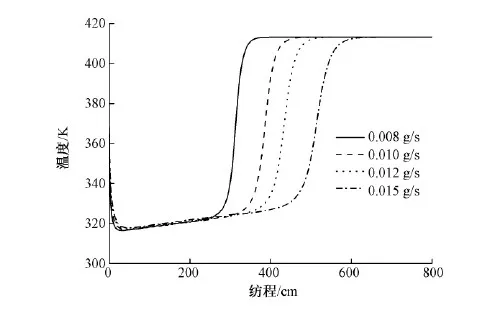
图4 泵供量对丝条温度的影响Fig.4 Effect of mass throughput on filament temperature

2.2.2 不同热风风速和温度对纺丝速度的影响

图5示出不同甬道风速对纺丝速度的影响。可见，在相同的初始张力下，在风速较小的情况下纺丝速度大。甬道风速增加使传热增加，丝条周围的溶剂含量降低，使纤维溶剂蒸发速率加快，并导致丝条的湿球温度略有下降，丝条拉伸黏度增加较快；并且风速的增加使得拉伸区丝条与空气的相对速度减小，使空气阻力项减小，丝条张力下降快，这些因素均使纺丝速度降低。因此在相同的纺丝速度下，甬道风的增加会使喷丝头处丝条张力增大，造成断丝现象，严重影响纺丝过程。对于高倍拉伸纺丝，喷丝头附近的风速不易过快。

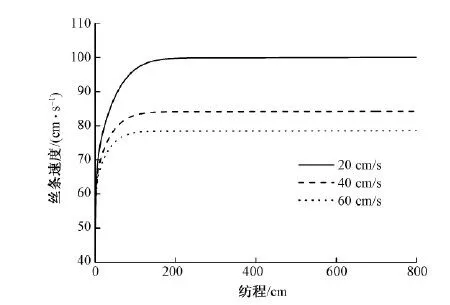
图5 不同甬道风速对纺丝速度的影响Fig.5 Effect of wind speed on spinning speed

图6示出不同甬道风温度对比纺丝速度的影响。可以看出，甬道风温度对纺丝速度的影响很小，甬道风温度的增加可以加强传热和传质，使丝条溶剂蒸发更快，丝条温度升高，在温度和溶剂含量的综合影响下使得丝条的拉伸黏度基本一致，纺丝速度没有太大变化。

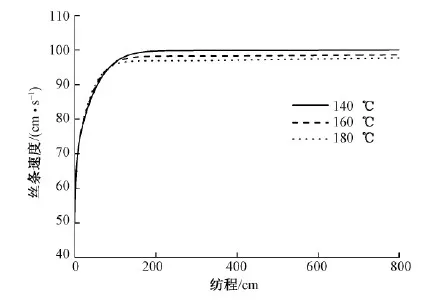
图6 不同甬道风温度对纺丝速度的影响Fig.6 Effect of wind temperature on spinning speed

2.2.3 不同原液浓度对丝条浓度的影响

图7示出原液浓度对丝条溶剂的影响。可见，原液溶剂含量增加，在原液泵供量和纺丝速度相同的情况下，所需要蒸发的溶剂增多，甬道内溶剂含量也相应增加，丝条达到同等固含量的时间变长，因此要想在较高的纺丝速度下丝条能较好地干燥，需将原液浓度控制在一定范围内。

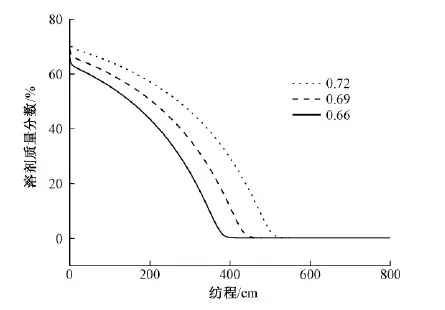
图7 原液浓度对丝条溶剂含量的影响Fig.7 Effect of solvent mass fraction on filament solvent content

2.2.4 不同纺丝速度对丝条溶剂含量的影响

图8示出纺丝速度对丝条溶剂含量的影响。可以看出，在相同的纺丝工艺下提高纺丝速度，丝条的溶剂含量下降较快，随着纺丝速度进一步提高，丝条中溶剂的蒸发速率增加趋势减缓。纺丝速度的提高可以使丝条变细，丝条与热空气的相对速度增大，传热和传质加强，更有利于溶剂从纤维内部扩散到表面，丝条干燥效果更好，但在较高纺丝速度时，纺丝速度的提高对溶剂蒸发速率的影响减小。由此可见，一定范围内提高纺丝速度不会降低甬道风对丝条的干燥效果。

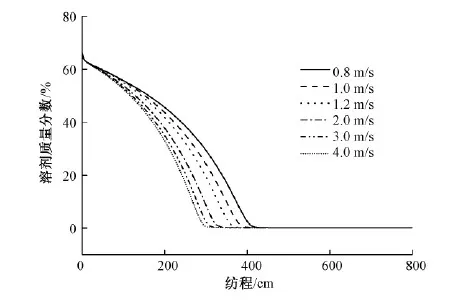
图8 纺丝速度对丝条溶剂含量的影响Fig.8 Effect of spinning velocity on filament solvent content

3 结 论

1)在聚乙烯醇顺流式干法成形过程中，温度的降低使丝条凝固，在纺丝速度较低的情况下，喷丝头处的张力最大。

2)泵供量的增加使甬道风对丝条的干燥时间增长，使丝条在纺程更远处凝固，丝条内溶剂含量是控制丝条温度变化的关键因素。

3)提高甬道风风速不利于纺丝速度的提高，而提高甬道风温度对纺丝速度的提高影响很小。

4)在相同泵供量和纺丝速度下，增加溶剂溶度会使溶剂的蒸发速率减慢，丝条不易干燥固化。

5)增加卷绕速度可以加强传热传质过程，使溶剂更快地从丝条中挥发出来，但在较高的纺丝速度范围内，丝条溶剂含量变化不大。

FZXB

[1] 李盛林, 秦峰. 水溶性聚乙烯醇纤维和聚乙烯醇干

法纺丝[J]. 维纶通讯, 2004, 24(4)：7-11. LI Shenglin, QIN Feng.Water-soluble polyvinyl alcohol fiber and dry spinning of polyvinyl alcohol[J]. Vinylon Communication, 2004, 24(4)：7-11.

[2] OHZAWA Y, NAGANO Y, MATSUO T. Studies on dry spinning： I: fundamental equations[J]. Journal of Applied Polymer Science, 1969, 13:257-283.

[3] OHZAWA Y, NAGANO Y. Studies on dry spinning: II: numerical solutions for some polymer-solvent systems based on the assumption that drying is controlled by boundary-layer mass transfer[J]. Journal of Applied Polymer Science, 1970, 14:1879-1899.

[4] SANO Y. Dry spinning of PVA filament[J]. Drying Technol, 1984, 2 (1):61-95.

[5] SANO Y. Drying behavior of acetate filament in dry spinning[J]. Drying Technol, 2001,19 (7): 1335-1359.

[6] GOU Z, MCHUGH A J. A comparison of Newtonian and viscoelastic constitutive models for dry spinning of polymer fibers[J]. Journal of Applied Polymer Science, 2003, 87:2136-2145.

[7] GOU Z, MCHUGH A J. Two-dimensional modeling of dry spinning of polymer fibers[J]. Journal of Applied Polymer Science, 2003,118 :121-136.

[8] YILMAZ L, MCHUGH A J. Analysis of nonsolvent-solvent-polymer phase diagrams and their relevance to membrane formation modeling[J]. Journal of Applied Polymer Science, 1986, 31:997-1018.

[9] SAKURADA I, NAKAJIMA A, FUJIWARA H. Vapor pressures of polymer solutions: II: vapor pressure of the poly(vinyl alcohol)-water[J]. Journal of Polymer Science, 1959,35:497-505.

[10] NIKOLAOS A, PEPPAS, EDWARD W, et al. Determination of interaction parameter χ1, for poly(vinyl alcohol) and water in gels crosslinked from solutions[J]. Journal of Polymer Science: Polymer Chemistry Edition, 1976,14 :459-464.

Simulation of dry spinning of PVA soluble fiber

WANG Jianquan, WU Jintian, LIU Pengqing, YE Guangdou, XU Jianjun

(StateKeyLaboratoryofPolymerMaterialsEngineering,SichuanUniversity，Chengdu,Sichuan610065,China)

A one-dimensional model of the downstream dry spinning was established. Using the corridor solvent balance equation combined with the momentum balance equation corrected by downstream drying process characteristics, the solvent content of the polyvinyl alcohol, temperature, speed,and the tension distribution in spinning line were simulated to predict the influence of the spinning parameters on spinning process. The results show that the filament experiences a longer equilibrium period in wet-bulb temperature after flash evaporation. The control of the filament temperature mainly depends on the solvent content of the filament. The filament has the largest tension in spinneret at the lower spinning speed. The increase of corridor wind is not conducive to improving the spinning speed. A larger winding speed is beneficial to the dry formation of the fibers.

polyvinyl alcohol fiber; dry spinning; spinning dynamics; computer simulation

0253- 9721(2013)02- 0023- 05

2012-08-31

2012-10-19

王建铨(1986—)，男， 硕士生。研究方向为聚乙烯醇水溶纤维。徐建军， 通信作者，E-mail: xujj@scu.edu.cn。

TQ 342.41

A