基于灵活度考虑的棉花异纤分拣机器人结构参数优化设计
沈丹峰,张华安,叶国铭,王贯超
(1.西安工程大学 机电工程学院,陕西 西安 710048;2.上海华迪机械有限公司,上海 201602;3.东华大学 机械工程学院,上海 201620)
近10年来,棉花异纤检测技术有了较大的发展,检测成功率有的已达80%[1-3]。现有异纤清除设备多数在纺纱工序中使用,如在清梳工序或络筒工序,这使纺纱流程复杂化,且需要进行相应设备改造。具有灵活移动特性的棉花异纤分拣机器人由于其作业空间小,无需更改现有纺纱流程而受到重视。在棉花异纤检测中,机器人的作用是实现棉花的抓取和分类堆放,其异纤检测通过藏于体内的传感器完成。通常,将棉包通过开棉机开松,开松的棉花堆放在堆棉台上,由于棉纤维的相互缠绕与松软,棉堆具有不确定的形状,需要制定出最佳抓取路径。相应地,机器人末端执行器应具有较好的灵活性,以满足不同抓取路径的要求。
在工作有限的空间,采用灵活度高的机械结构是选择机器人机构需要考虑的一个重要因素,不同的关节转角和机械臂长度会影响机器人末端执行器的灵活度。较多的关节具有较大的灵活度,但这也会带来控制的复杂化。采用数值或几何的方法针对不同应用领域的机器人构型来求解其灵活工作空间是目前多数研究者选用的方法[4-5]。本文从棉花抓取需要出发,介绍了一种五自由度棉花异纤分拣机器人结构,分析了机器人的工作空间及其灵活性,并提出基于灵活度考虑的结构参数优化方法,最后通过模拟实验验证机器人的灵活性满足抓取要求。
1 机器人运动学
1.1 机器人结构
设定棉花异纤分拣机器人基本工作条件如下:1)机械手一次抓取棉花质量小于0.5 kg;2)棉纤维属于软体物质,机器人重复抓取精度要求不高;3)棉花堆放在尺寸为2 m×2 m×0.3 m的堆棉台上。
根据上述要求,结合通用关节机器人的常用结构,设计出机器人机体结构。
1)选择关节型机械臂,包括腰部、大臂、小臂3部分。其动作灵活,工作空间大,占地面积小。
2)为减小机械臂尺寸与质量,在腰部增加升降机构,在垂直方向增加作业空间。
3)在小臂添加伸缩关节,此关节扩大抓取空间。
4)为了能够让棉团由腕部吸入,同时降低机器人的控制难度,机械手腕部无自由度。
5)采用四轮小车,移动灵活。
棉花异性纤维分拣机器人结构示意图如图1所示[7]。
选用五自由度串联关节型机械手 PRRRP,3个关节是转动副,2个关节是移动副。通常,棉包中的棉花挤压密实,需要经过开棉机开松后才能由机器人末端执行器7抓取,末端执行器根部开有吸棉孔,将抓取的棉花通过小臂6、大臂5、腰部4中的内置孔吸入到收集袋2,在小臂和大臂的棉流通道处安装有传感器,用于识别异性纤维。若发现异性纤维,则将该棉花归为含异性纤维棉团,通过机械臂内置孔中的导向阀收集到收集袋中;若未发现异性纤维,则将该棉团导出到正常棉堆中。这样经过分拣后,人工只需处理收集袋中的棉团,可大大降低工作量。
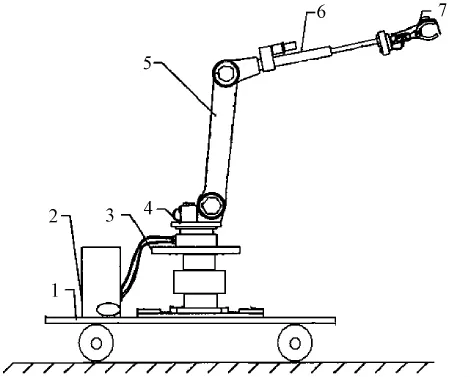
图1 机器人示意图Fig.1 Robot schematic diagram
1.2 运动学方程正解
机器人末端执行器在机器人基坐标系中的位姿可用Denavit和Hartenberg提出的杆件坐标系的矩阵方法表示[6],棉花异纤分拣机器人的杆件 D-H坐标系如图2所示。
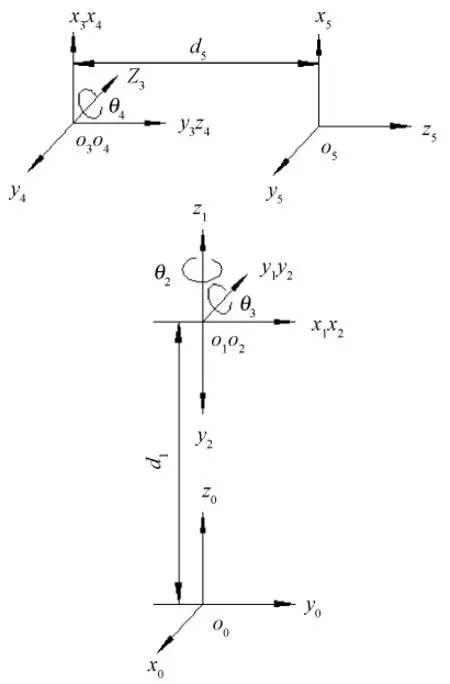
图2 机器人D-H坐标系Fig.2 D-H coordinate system of robot
机器人的结构参数见表1。di为移动变量,θi为第i个关节的关节转角,ai为第 i个杆件杆长,γi为第i个关节与第i-1个关节的夹角。各关节变量的边界约束可采用作图法获得。

表1 机器人D-H参数Tab.1 D-H parameters of robot
通过坐标系的依次平移与旋转,可以获得各杆件坐标系之间的变换矩阵Ai,将各个变换矩阵相乘得到末端执行器相对于基坐标的位姿。由相邻杆件的D-H参数得到的机器人末端执行器相对基坐标系的变换矩阵为
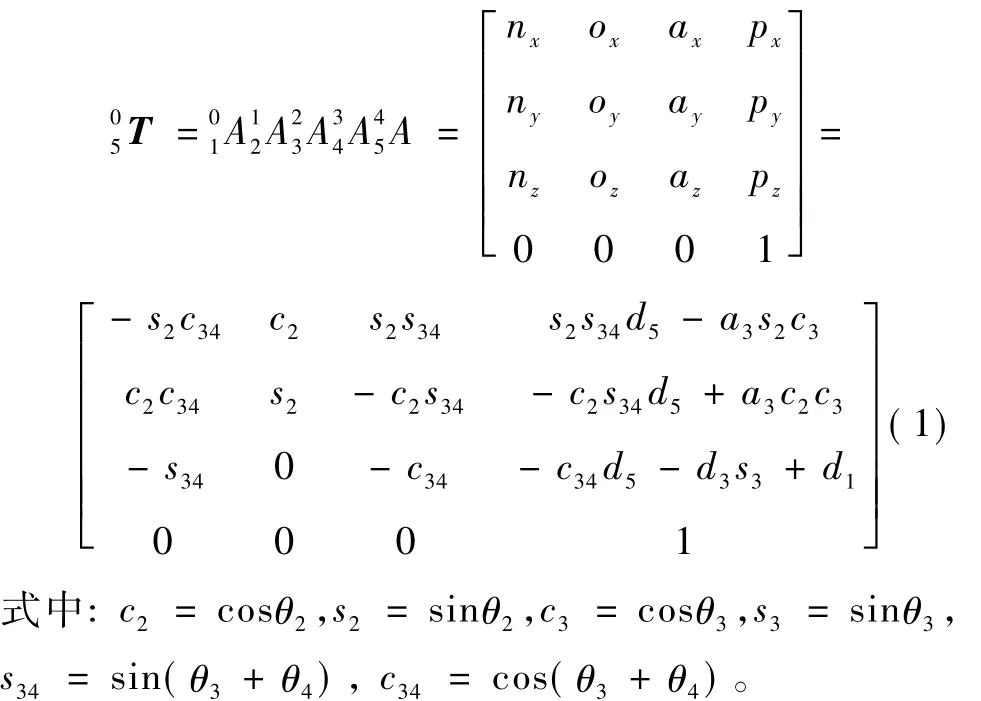
1.3 运动学方程逆解
机器人的关节变量(d1,θ2,θ3,θ4,d5)可通过机器人逆运动学方程求解得到,由机器人杆件坐标系可知,机器人末端执行器的位置可用末端执行器姿态矩阵中的方向向量p表示,因此,机器人的轨迹控制需要通过该向量反求关节变量,方程可以简化为
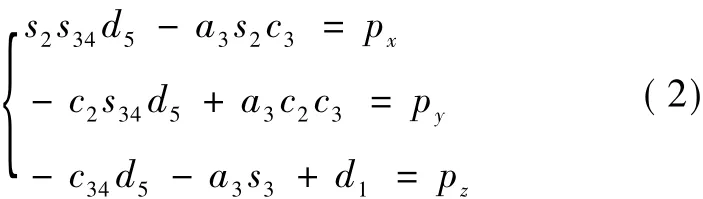
该方程组由3个方程构成,含有6个未知量,能达到该位置的机器人姿态存在自由解,不考虑抓取姿态,该机器人属于冗余结构,存在多解。假定自由变量是 d3、θ3和 θ4,根据该方程,当自由变量取为确定值时,剩余 3个关节变量会有 4组解,如式(3)、(4)所示。

2 工作空间与灵活性
2.1 工作空间分析
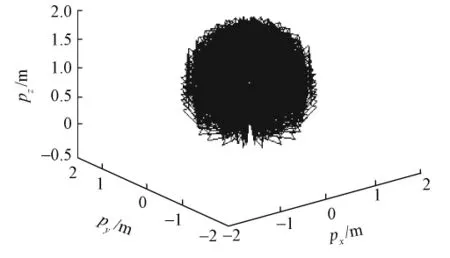
图3 末端执行器工作空间Fig.3 Work space of end effector
采用数值法计算机器人的抓取空间。根据机器人机械臂的结构尺寸,将各关节变量在其运动限位范围内离散化,运用机器人的正运动学方程解遍历离散化后的所有组合得到机器人末端位置坐标即是工作空间,见图3。
2.2 灵活性分析
腕部无自由度的棉花异纤分拣机器人要求在棉堆空间内具有足够的灵活性以满足多方位的抓取动作。由机器人逆运动学公式可看出,1个确定的末端位置矩阵对应若干组关节变量。当关节变量的值超出运动范围时,则该位姿不能实现。机器人末端执行器在工作空间内所能实现的姿态越多,机器人灵活性就越高。以抓取点 P坐标(0.3,0.3,1)为例,考虑到关节运动精度,对自由变量在工作范围内以间隔1°遍历所有解,有303组关节变量能够满足。然而,棉花异纤分拣机器人的抓取动作是由抓取点要求的位姿决定的,即末端执行器要以一定的姿态达到抓取点,通常,取D-H坐标系变换矩阵中的导航向量a作为考核灵活性的指标,即在抓取点能够有多少种姿态到达。
将机器人末端执行器的手指看作空间向量,为描述手指的灵活度,引入服务球和服务区的概念[9-10],如图 4 所示。
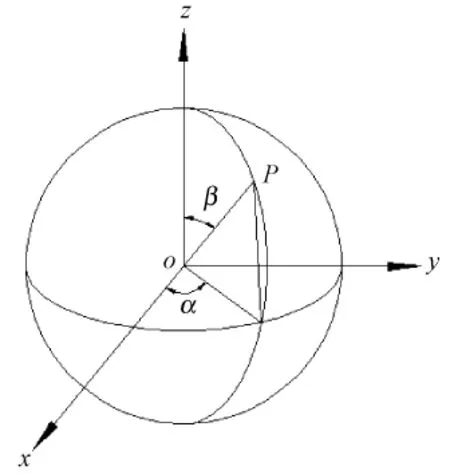
图4 服务球Fig.4 Service ball
服务球是以指尖为圆心,以单位长度为半径形成的球。
服务区是服务球上的每点对应1种机器人末端姿态,所有可达点集合组成的区域。
服务区的面积和整个球表面积的比值称为此圆心点O的灵活度。若将服务球离散化,那么,服务区所包含的离散点数称为灵活点数,因此,灵活点数越多,灵活度越高。
对半球面上的点进行离散化,用极坐标描述分别对α、β等步距取点,以球面上的点P为姿态向量的起点,球心O为终点,姿态向量PO的表达式为
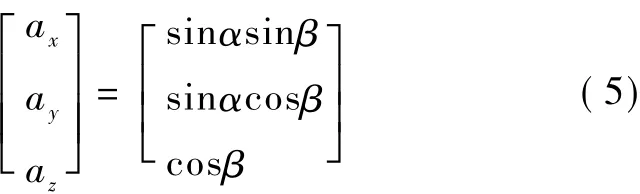
考虑抓棉动作只能由棉堆外侧进入抓棉点。参考基坐标,α和β取值范围应为[0,π]。
以工作空间内的任意一点分析其灵活性。取点(0.3,0.3,0.6)为例,分析结果见图5。图中符号“·”表示能够实现的姿态,符号“x”表示不能实现的姿态。棉花异纤分拣机器人通过视觉传感器或人工远程监控获得抓取点坐标,通过对此点的灵活性仿真可以辅助操作者或机器人自动选择最佳抓取姿态。
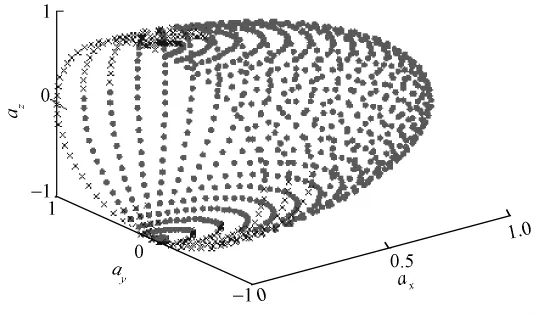
图5 机器人空间灵活点仿真Fig.5 Flexible point simulation in robot workspace
3 结构参数优化
为了达到以较小的关节自由度满足抓取功能要求的目的,提出以灵活点数最大为评价指标的机器人结构参数优化设计。优化方法是以棉堆半剖面为工作面(见图 6)[7]。
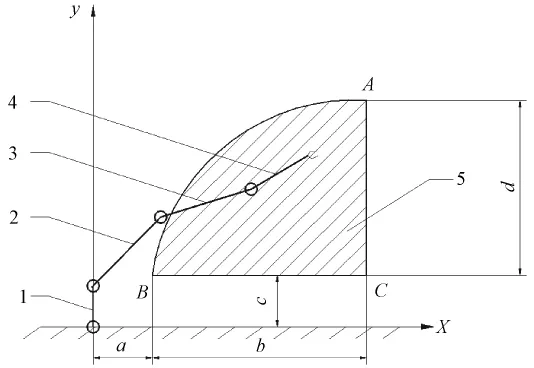
图6 棉堆半剖面Fig.6 Semi-section of cotton pile
图中,a=0.2 m,b=1 m,c=0.3 m,d=1 m。由工作空间分析可知,d1、a3、d5是工作空间包络线的主要影响尺寸。根据仿生学原理,大臂与小臂基本相等,小臂伸缩关节行程为小臂长度的一半,依据抓棉量,确定末端执行器轴向长度为0.3 m,因此,该问题的影响因素就只有d1和a32个变量。已知d1边界约束为[0.3,1.3],a3边界约束为[0.54,0.69],其满足棉堆半剖面所有位置抓取要求。以机器人在棉堆半剖面中抓取点的灵活度最大为目标函数,初始点在可行域内任选,按照机器人关节实际精度遍历所有抓取姿态,由于按照实际精度进行计算,计算量将会是非常巨大的。为了缩小计算量,将d1精度取为0.1 m,a3精度取为0.02 m,单位球半径精度取为0.2 m,关节角精度取为10°。以灵活性为优化对象的数学模型为
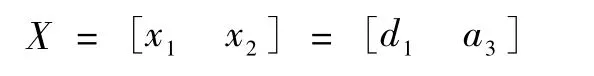
1)目标函数是在棉堆半剖面内机器人可行姿态的数量,为

式中:x,y,z为指尖抓取点位置;d 为采样步长;α,β为末端执行器的姿态;a,b为 α和 β在区间[0,180°]内以步长d采样所取的点数。
2)约束条件为
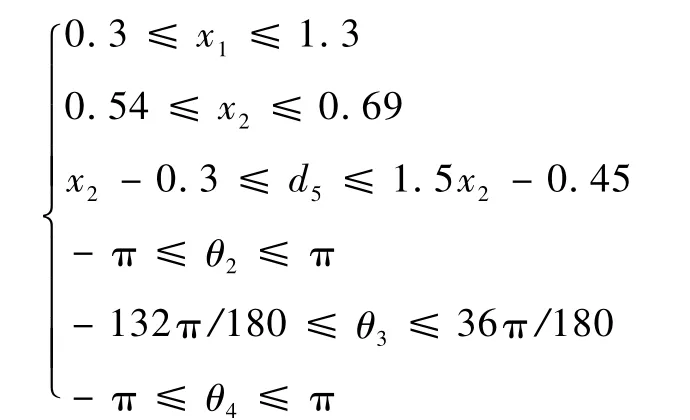
运用MatLab软件编程优化计算。图7示出灵活点数结果随 d1和 a3的变化趋势。其最优解是x1=1.3 m,x2=0.69 m。即此时具有最大的灵活性,灵活点数为262个,较采用最小机械结构尺寸的灵活度26个高出10倍。可以预见,当采用实际工作精度,其灵活度会更高。
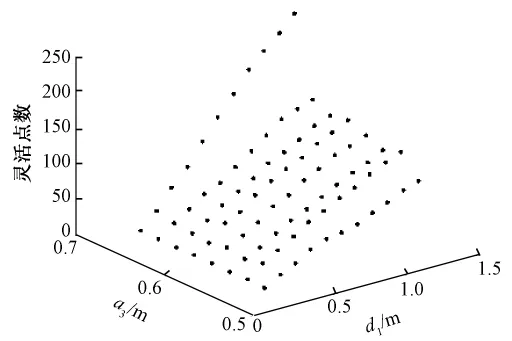
图7 随d1和a3变化的灵活点数Fig.7 Flexible points with d1and a3
4 虚拟样机试验验证
采用具有最大灵活点数的关节参数,利用solidworks将机器人的工作空间主剖面旋转生成三维模型,并与棉堆空间进行对比,如图8所示。可直观发现末端执行器工作空间完全覆盖了一半的棉堆空间,这样机器人只要通过移动到棉台另一侧即可完成棉堆空间的全覆盖。
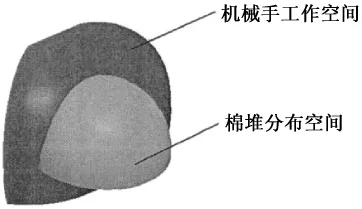
图8 空间对比图Fig.8 Space contrast figure
采用ADMAS软件,将机器人模型导入,在模拟环境下,任取手术空间中的1点,给出此点样本姿态的范围,在可达姿态范围内选择试验姿态,并控制机器人实现此姿态,表2示出点(0.5,0.4,0.7)的灵活性试验数据。根据样本姿态仿真结果,共有100个姿态能够达到。选择5个姿态在ADMAS环境下进行试验,机器人成功实现了所选姿态。

表2 模拟试验数据Tab.2 Data of simulation test
5 结论
考虑灵活度最大的机器人结构参数的优化方法,使少自由度的机器人能够获得一定的姿态冗余,对于降低成本与控制难度都是有益的。针对目标抓取物是对称的或抓取方向不作要求的设计问题,采用灵活度最优的设计方法可以减少关节数而保证最大的灵活度。其设计方法归纳如下:
1)采用几何法确定机器人各关节的边界约束。
2)建立运动学方程,得到位置方程。
3)将位置方程中冗余变量取作自由解,解出剩余变量。
4)在约束域遍历冗余变量,以确定的抓取空间为对象,统计剩余变量可行解的个数,取可行解最多的关节变量作为最优解。
[1]王季,陆文凯.线阵相机场曲复原及在异纤检测中的应用[J].光学精密工程,2009,18(9):2116-2121.WANG Ji,LU Wenkai.Restoration of field curved image from line camera and its applications in foreign fiber detecting [J].Optics and Precision Engineering,2009,18(9):2116-2121.
[2]陈志国,须文波.一种机器视觉异纤高速清除系统[J].计算机工程与应用,2010,46(10):199-201.CHEN Zhiguo,XU Wenbo.High-speed foreign fiber detecting and clearing system with machine vision[J].Computer Engineering and Applications, 2010,46(10):199-201.
[3]阎磊,郝爱萍,王志鸿.异纤的危害及清除方法探讨[J].棉纺织技术,2012,39(12):772-775.YAN Lei,HAO Aiping,WANG Zhihong.Discussion of foreign fiber harmfulness and elimination method[J].Cotton Textile Technology,2012,39(12):772-775.
[4]LAI Z C,MENG C H.The dexterous workspace of simple manipulators[J].IEEE Journal of Robotics and Automation,1988,4(1):99-103.
[5]黄献龙,梁斌.分解法求解EMR系统机器人的服务角[J].中国空间技术,2001(4):63-67.HUANG Xianlong,LIANG Bin.Solving the service angle ofEMR system robotwith a decomposing method[J].Chinese Space Science and Technology,2001(4):63-67.
[6]熊有伦.机器人学[M].北京:机械工业出版社,1993:10.XIONG Youlun.Robotics[M].Beijing:China Machine Press,1993:10.
[7]沈丹峰,赵辉,叶国铭.棉花异性纤维分拣机器人总体结构的优化设计[J].东华大学学报:自然科学版,2012,38(3):87-90.SHEN Danfeng,ZHAO Hui,YE Guoming.Optimizeddesign for different fibers sorting robot structure[J].Journal of Donghua University:Natural Science Edition,2012,38(3):87-90.
[8]MAYORQA R V,CARRERA J,ORITZ M M A.Kinematics performance index based on the rate of change of a standard isotropy condition for robot design optimization[J].Robotics and Autonomous Systems,2005,53(3):153-163.
[9]邢宏光,王利宏,张玉茹.神经外科手术机器人灵活性分析[J].北京航空航天大学学报,2004,30(4):312-315.XINGHongguang, WANG Lihong, ZHANG Yuru.Dexterity analysis of robot for neurosurgery[J].Journal of Beijing University of Aeronautics and Astronautics,2004,30(4):312-315.
[10]崔建昆.3-RRR平面并联机器人的灵活工作空间[J].上海理工大学学报,2005,27(4):365-368.CUI Jiankun.On the dexterous workspace of 3-RRR planar parallel manipulator[J].Journal of University of Shanghai for Science and Technology,2005,27(4):365-368.

