叠加原理法在建设项目水资源论证中的运用

连明涛

叠加原理法在建设项目水资源论证中的运用

随着社会经济的发展，用水量的需求也随之增加，所以在建设项目取水水源论证中，特别是在地下水水源论证中，单井供水的情况越来越少。单井供水在满足一定水量要求的条件下，不但要增加资金的投入，而且很容易引起地下水环境的变化，甚至引起地质灾害。所以现在的很多项目工程，一般都是以井群的方式给项目工程联合供水，这样不但能解决水量的需求，而且也能够避免地下水环境的恶化。所以在做地下水水资源论证时，首先要看项目工程的取水方式，是单井供水还是井群供水，如果取水方式是单井供水，在论证方法上就很容易选择；如果取水方式是井群，每眼井同时取水，井间距离小于影响半径，这样井彼此间的降深和流量都要发生干扰。对于这样的问题，如果每眼井都分别进行分析计算，就会增加计算工作量，如果选用其他论证方法，在资料的收集、论证范围的确定等方面，不但有很大不确定性，而且也会影响论证结果的精确度和准确度。

针对这一问题，笔者在实践中利用线性定解问题解的叠加原理，来解决水资源论证中干扰井群联合供水的问题，叠加原理具有很强的实用性。

一、叠加的基本原理

连明涛

式中α、β为上述边界的已知函数，这种类型的边界条件称为第三类边界条件（也就是在研究区的边界上如果分布有相对较薄的一层弱透水层（带），边界的另一侧是地表水或一个含水层分布区时，可以看作是此类边界）。这些方程和表达式可改写为：

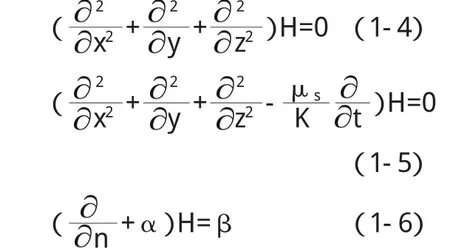
以上三式中的左端括号内部分，代表一个运算符号，它对水头H进行某种运算，称为算子。通常用L来表示。如果对水头H的任意两个H1和H2的线性组合C1H1+C2H2，恒有

则称L为线性算子，式中C1、C2为任意常数，式（1-4）～（1-6）都是线性算子。利用线性算子，可把线性偏微分方程的定解问题用下面的简单表达式表示

上式B中为边界条件的线性算子。D为渗流区。Γ为流域的边界。方程（1-8）中没有包含与水头H无关的项，方程是齐次的。边界条件（1-9）是非齐次的。如果偏微分方程中包含了入渗量W（x、y、t）或其他与水头H有关的项，则方程是非齐次的，表示为

叠加原理可表述如下：L（H）=0是关于H的线性齐次偏微分方程，H1和H2是它的两个解，C1和C2是两个任意常数，则线性组合

也是该方程的解。

一般地说，如Hi（i=1，2，…，n）是方程L"#

H=0特解，则

也是该方程的解，式中Ci为任意常数。

二、承压水和潜水叠加模型的建立

因为承压水和水平流动的半承压含水层中水的流动方程是线性的，所以对于任意布置的相互干扰的完整井群的稳定运动，可以直接应用叠加原理。假设在渗流区中有n口井任意排列并相互发生干扰。各井的抽水量Qj（j=1，2，…，n）为常数。设si代表位于（xi，yi）处的观测孔由于各井抽水引起的总降深，sij代表第j口井单独抽水时在观测孔i引起的降深。当边界条件为齐次时（如抽水前的初始水头和边界水头H0为常数，因而s=0），根据叠加原理，有

对于承压水的稳定流，有

式中：Qj——第j口井的抽水量，如为注水井，则取负值；

Rj——第j口井的影响半径；

rij——观测口i到抽水井j的距离；

T——含水层的导水系数。

如果有n个观测孔，则对于观测孔 i=1，2，…，n分别写出（2-2）式，得一线性方程组

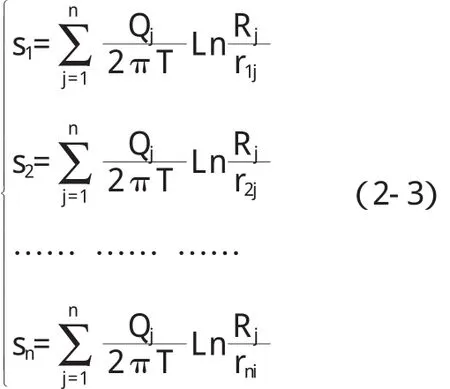
当Rj和rij已知时，可由一组已知的Qj值求出si值。通常把抽水井当作观测孔，并假设井壁就是等势面。在（2-3）式中，只要当 i=j时令 rij=（rw）j代表各井的半径，相应的si代之以各抽水井的降深swi，也可由给定的各井流量Qj值求出各井的降深swi。

对于井群位于具有水平隔水底板的潜水含水层中，由于潜水的运动方程是非线性的，应用dupuit假设，则可对H2-h2进行叠加，有

式中：hi——观测孔（坐标为xi，yi）中的潜水含水层厚度；

H0——抽水前潜水含水层的初始厚度；

K——含水层的渗透系数；其余符号同前。

根据叠加的基本原理，由于潜水井群初始条件和边界条件为非齐次的（即h＝H0而不是h=0），因而不是直接对h2进行叠加，而是对H02-h2进行叠加。

三、应用实例

以河南省襄城县第二水厂给水工程集中开采水源地水资源论证为例。该建设项目日开采地下水3万m3，水源地拟建在襄城县区域内北汝河南部，水源井集中布设，设计18眼取水井，井径0.3m，井深50m。

边界条件：水源地北侧是北汝河，南侧2000m以外是相对高程150m左右的首山，东西两侧是相对平缓的平原区，地势西高东低，这样北侧北汝河作为补给边界来处理，南侧由于其距离大于影响半径，所以不作为隔水边界来处理，该边界类型属于边界条件中的第三类边界条件，又由于井间距是300m，小于影响半径R=600m，井群相互干扰。因此，笔者运用叠加原理对水源地布置的井群进行叠加，以此计算井群的降深。

根据论证区地下水水文地质条件，上部是由4m左右较薄的亚粘土和亚砂土所覆盖，下面是8m左右的中砂含水层，然后是6m左右的亚黏土隔水层，下面又是20m左右中砂、砂卵石、卵砾石互间含水层，这也是水源地的主要含水层和取水层，具有层压性，在取水过程中该层接受上面含水层越流补给，在井底是一层具有隔水性能的亚黏土夹亚砂土层。从水文地质勘测报告中可知含水层、隔水层，厚度分布比较均匀，含水层具有导水性能强等特点。根据地下水动力学原理，可将此地下水概化为均质各向同性，产状水平，一侧有补给边界的越流含水层，井之间互相干扰的完整井层压稳定流模型。

根据越流的基本微分方程：

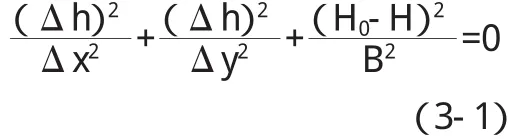
根据论证区水文地质和边界条件：

运用干扰井群叠加法，对降深s进行叠加计算，各井的抽水量为Qj（j=1、2、…、n）为常数，设Si代表位于（xi，yi）处的观测孔由于各井抽水引起的总降深，Sij代表第j口井单独抽水时在观测孔i引起的降深，当边界水头为齐次时，根据叠加原理

式中：

Q——单井出水量（m3/d）；

s——以固定流量Q抽水时与抽水孔距离为r处任一时间t的水位降深（m）；

T——含 水 层 导 水 系 数（m2/d）（T=486.24m2/d）；

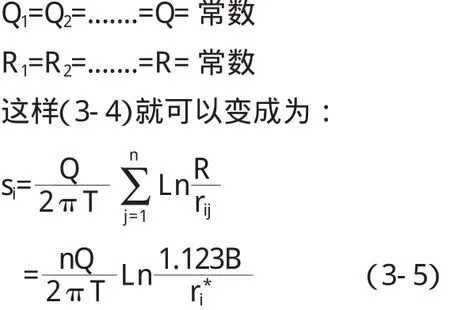
Qj——第j口井的抽水量（m3/d）；

Rij——观测孔i到抽水井j的距离（m）；

si——在（Xi，Yi）处各井抽水引起总降深（m）；

sij——抽水井（Xj，Yj）处在（Xi，Yi）处的抽水井引起的降深（m）。

根据项目工程运行后近几年的水源地水位稳定后的实际情况来看，近几年水源地的中心水位降深一般是维持在13m左右，由此可见笔者运用干扰井群叠加法对该水源地进行的水资源论证可行的，完全能够满足工作的需要

平顶山水文水资源勘测局 467001）