基于BP神经网络的地下空间温湿度预测

葛珂楠，程忠庆，赵云鹏

（海军工程大学 勤务学院，天津300450）

0 引 言

地下空间的开发是解决城市地上空间不足和环境危机的有效途径。地下空间很容易产生潮湿的问题，不仅会导致设备腐蚀失效，长期居住还会严重影响身体健康。除湿机在地下空间中被普遍使用，所以能够保证除湿机正常运转，准确预测故障显得尤为重要，一直为人们所关注。

地下环境是一个系统，设备工作条件下的环境温度和湿度等参数之间存在一定的函数关系，只要有精确的系统模型就可以利用历史数据预测出未知的参数数据。这些数据可以为除湿机的故障预测和诊断提供支持。但由于系统的强耦合性和强非线性以及受多个环境因子相互影响，建立数学模型精确预测温度和湿度存在难度。

BP神经网络具有并行计算、分布式处理、自组织和自适应能力，非常适合处理多因素相互影响，非线性条件下的信息处理问题。对系统建模结构和动态性方面知识要求不多，只需要获取样本的输入和输出，就能利用网络的学习能力得出数据之间的非线性关系。基于此，本文采用神经网络中的BP网络对地下空间中的温度和湿度进行预测。

1 BP神经网络原理

BP神经网络也称为误差反向传播 （back propagation）神经网络，是一种多层前向型神经网络。在BP网络中，信号是向前传播的，而误差是反向传播的。与 Windrow－Hoff学习算法相似，标准的BP神经采用梯度下降算法，网络权值沿着性能函数的梯度反向调整，能够对有限不连续点的函数进行逼近。

应用最为广泛的神经网络具有多层的网络结构，含有一个或更多的隐层。层与层之间的节点采用全互联的连接方式，每层内节点之间没有联系。以含有一个输入层，一个隐含层和一个输出层的三层BP神经网络为例，其网络结构如图1所示。

图1 BP神经网络结构

BP算法要先将输入信号向前传播到隐含层节点，经传递函数后，把信号传播到输出节点，最后得到输出结果。BP网络通常采用Sigmoid函数或线性函数作传递函数。Sigmoid函数表达形式如

经传递函数运算后得到的输出值与期望值进行比较，如果存在误差，则将误差反向传播，然后根据误差梯度下降法来调节各层的权值和阈值，使修改后的网络的最终输出能接近期望值。对于每一个样本m的二次型误差函数Em为

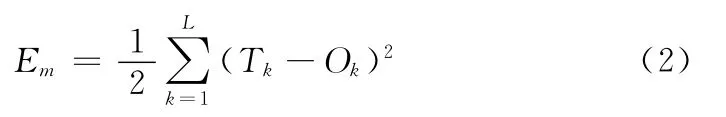
系统对P个训练样本的总误差函数为

式中：L——输出层神经元个数，Tk——节点期望输出值，Ok——节点计算输出值，P——训练样本个数。

逐层求出目标函数对各神经元权值的偏导数，构成目标函数对权值向量的梯度向量，作为修改权值的依据。不断通过循环减小误差直到输出满足要求为止。

2 BP网络模型的建立

2.1 网络参数确定

网络输入层神经元节点数就是系统的特征因子个数，输出层神经元节点数就是系统目标个数。隐层节点数按经验选取，设置网络隐层节点数目为8个，训练时还要对不同的隐层节点数分别进行比较，最后确定出最合理的网络结构。模型运行参数设置见表1。

如表1所示，学习速率影响着收敛速度和系统的稳定，倾向于选取较小的学习速率以保证系统的稳定性，该值一般取0.010.8。动量因子一般取0.60.8，允许误差一般设置在10－310－5之间，这里设置允许误差为10－4，当迭代误差小于该值时，结束迭代计算。迭代次数我们取2000次以保证在不收敛的情况下允许最大的迭代次数。Sigmoid参数调整神经元的激励函数形式，通常取0.91.0。

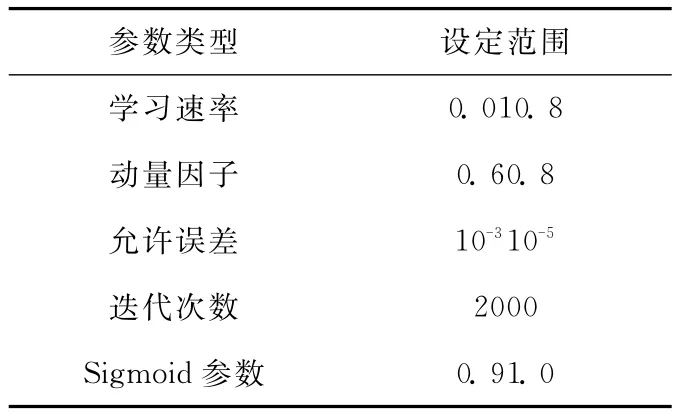
表1 BP神经网络模型参数设置

2.2 算法选择

标准的BP学习算法是梯度下降法，它的计算的复杂度主要是由计算偏导数引起的。但是这种基于梯度下降方法的线性收敛速度很慢，而LM （levenberg－marquardt）算法是一种利用标准的数值优化技术的快速算法。和拟牛顿算法一样，LM算法也是希望在不计算Hessian矩阵的情况下获得高阶的训练速度。误差性能函数可以表示为平方和的形式如

此时Hessian矩阵可以近似为

而梯度为

式中：p——样本数目，w——网络权值和阈值所组成的向量；e（w）——实际输出向量与期望输出向量之间的误差；J （w）——Jacobi矩阵。其中Jacobi矩阵可以通过标准的BP算法得到，其表达式为

Levenberg－Marquardt算法的更新过程与牛顿算法类似，应用了上述方法来近似计算Hessian矩阵。公式表达如下

式中：△w＝wk＋1－wk，wk＋1和wk和分别表示第k＋1和第k次迭代的权值和阈值所组成的向量；I——单位矩阵；μ——定 义 的 学 习 速 率；J （w）——Jacobi 矩 阵；e（w）——误差。

Levenberg－Marquardt算法是梯度下降法与牛顿法的结合，既有牛顿法的局部收敛性，又具有梯度法的全局特性，算法的目的就是尽快转换为牛顿法。由于LM算法利用了近似的二阶导数信息，所以LM算法比梯度法快得多。MATLAB工具箱提供了函数trainlm以实现Levenberg－Marquardt算法，本文用LM算法对网络进行训练。

3 定义训练样本

3.1 训练样本的选取

经过对某地下工程温度和湿度的定期监测，结合除湿机工作条件下的温湿度变化特性，本文选取了同时段温度和湿度数据样本各50组，每组数据按时间序列排列40个。即温度样本k组Tk（k＝1，2，…，50），在Tk下40个温度样本值序列分别为＝ ［，…，］（i＝1，2，…，40）。湿度样本k组Hk（k＝1，2，…，50），Hk下40个湿度样本值序列分别为k＝ ［，…，］（j＝1，2，…，40）。其中与为同一时间监测相互对应的数据组。在Tk和Hk下分别进行50次采样，分别获得2000个全部样本值，则可以得到全部样本输入矩阵为I＝［，］T，样本输出矩阵为O＝ ［原字符串］T，其中与为温度和湿度的预测数据组。

以其中一组温度和湿度数据为例，在相同时间序列下，该组温度和湿度的变化趋势曲线如图2和图3所示。

3.2 数据归一化处理

为了满足BP神经网络的输入要求，减小输入样本之间量纲差异对结果的影响，以达到网络最优化预测的目的，在网络训练之前要对数据进行预处理，即对输入数据进行归一化。让输入样本都处在 ［0，1］或 ［－1，1］区间内，这样可以提高训练效率。

本文采用基于最大值－最小值的数据处理方法，设温度样本归一化后的数据为（k＝1，2，…，50），则有

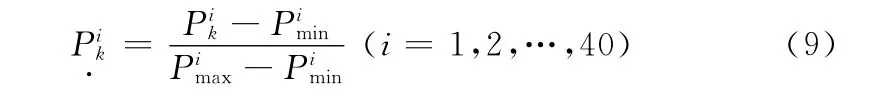
式中：——温度采样序列的最小值；——采样点序列的最大值。同样设湿度样本归一化的数据为（k＝1，2，…，50），则有

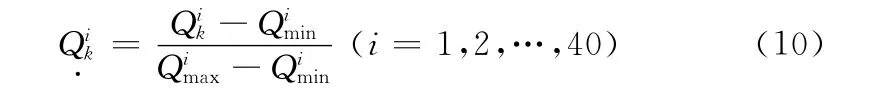
式中：——湿度采样序列的最小值；——采样点序列的最大值。

将归一化后的数据代入输入矩阵，这样我们就可以得到具有4000个样本的归一化输入矩阵I′。

4 温度与湿度预测

将建立的BP网络模型应用于测试样本集，用于检验该地下工程温度和湿度的预测精度情况。如图4所示，图为预测温度与实际温度比较示意图，其中，用 “＊”代表实际温度，用 “o”代表预测温度。

图4 某地下工程温度预测结果

从图4可以看出，预测温度与实际温度并没有很好的吻合。这是由于三层网络模型中，隐层神经元数目对预测结果影响很大。同时为了极小化目标函数，学习速率应选择足够小，否则会导致学习过程的震荡从而收敛不到期望解。因此调整隐层神经元数目至12个，适当减小学习速率后，预测温度与实际温度比较如图5所示。

图5 改进后的温度预测结果

由图5中可知，此时预测温度可以较好的拟合实测温度；图6为温度训练过程中的误差变化曲线。训练迭代36次后即达到了误差性能目标。

图6 网络训练中误差变化曲线

用上述方法对湿度的网络预测模型进行调整，将其隐层神经元数目增加至13个，相应减小其学习速率，得到湿度的预测与实际比较示意图，如图7所示。

图7 改进后的湿度预测结果

图7中，用 “＋”代表实际测量湿度，用 “o”代表预测湿度。可以看到预测湿度与实际湿度也十分吻合，达到了预期的效果。

5 预测结果分析

在该网络预测模型中，每个预测温度和湿度数据值都可以和前4个时间单元的实测数据值找到对应的非线性关系。利用网络模型对50组温度和湿度数据进行预测计算，然后将预测值与实测值进行对比与分析。本文使用标准偏差 （S）、偏差系数 （Cv）、期望偏差百分数 （EEP）和预测准确率 （P）这几个指标来评价预测值偏离实际值的程度，公式如下

式中：xk和xk′——预测值和实际值，珚x——实测值的平均值，xk，max——实测值中最大值。训练对比分析结果见表2。

表2 BP神经网络训练预测结果分析

由表1可以看出，偏差系数和期望偏差百分数都在3%左右，预测准确率在97%以上，具有比较高的精度，但在预测计算中仍有少量较大误差存在的情况。从程序的运行角度来看，因为目标函数陷入局部极小值，使预测值未得到最优解，或者因为该局部极小值未达到设置精度，使程序陷入死循环而不能收敛。正是这些原因限制了神经网络的预测精度。

6 结束语

本文在分析地下工程温度和湿度变化特性的基础上，提出了利用BP神经网络对温度和湿度预测的方法。经理论分析和结果验证，BP神经网络可以准确预测未来时刻内的温度和湿度状态趋势。同时，随着监测数据的不断增多，模型的精度也不断提高。该预测方法的实现为地下空间除湿系统的优化控制和故障诊断奠定了基础。

：

［1］LI Yanru，CHENG Zhongqing，JIANG Haibo.Dampproof engineering test of underground cavern and effect evaluation ［J］.Construction Technology，2011，40 （3）：91－93 （in Chinese）.［李艳茹，程忠庆，姜海波.地下洞库防潮工程试验及效果评估 ［J］.施工技术，2011，40 （3）：91－93.］

［2］TIAN Lin，WANG Long，YU Hang，et al.Interpolation of missing precipitation data base on BP neural network［J］.Journal of Yunnan Agricultural University，2012，27 （2）：281－284（in Chinese）.［田琳，王龙，余航，等.基于BP神经网络的缺测降水数据插补 ［J］.云南农业大学学报，2012，27 （2）：281－284.］

［3］YANG Liu，CHEN Yanping.A new globally convergent Levenberg－Marquardt method for solving nonlinear system of equations［J］.Mathematica Numerica Sinica，2008，30 （4）：388－396（in Chinese）.［杨柳，陈艳萍.求解非线性方程组的一种新的全局收敛的 Levenberg－Marquardt算法 ［J］.计算数学，2008，30 （4）：388－396.］

［4］JIANG Chengke.Application of neutral network based on genetic algorithm in dam displacement forecast ［D］.Dalian：Dalian University of Technology，2008 （in Chinese）.［姜成科.基于遗传算法的神经网络在大坝变形预报中的应用 ［D］.大连：大连理工大学，2008.］

［5］ZHANG Xudong，LI Yunze.Temperature prediction for nano satellite on orbit based on BP neural network ［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34（12）：1423－1427 （in Chinese）.［张旭东，李运泽.基于BP神经网络的纳卫星轨道温度预测 ［J］.北京航空航天大学学报，2008，34 （12）：1423－1427.］

［6］MA Li.MATLAB mathematics experiment and modeling［M］.Beijing：Tsinghua University Press，2010 （in Chinese）.［马莉.MATLAB数学实验与建模 ［M］.北京：清华大学出版社，2010.］

［7］FU Huixuan.MATLAB neural network application design［M］.Beijing：China Machine Press，2010 （in Chinese）.［傅荟璇.MATLAB神经网络应用设计 ［M］.北京：机械工业出版社，2010.］

［8］ZHUANG Chuqiang，HE Chunxiong.Application statistical basis ［M］.Guangzhou：China Science and Technology University Press，2011 （in Chinese）.［庄楚强，何春雄.应用数理统计基础 ［M］.广州：华南理工大学出版社，2011.］

［9］SUN Yu，ZENG Weidong，ZHAO Yongqing，et al.Model prediction of processing－property of TC11titanium alloy using artificial neural network ［J］.Rare Metal Materials and Engineering，2011，40 （11）（in Chinese）.［孙宇，曾卫东，赵永庆，等.基于BP神经网络的TC11钛合金工艺－性能模型预测 ［J］.稀有金属材料与工程，2011，40 （11）：1951－1956.］

［10］ZHAO Ying，NAN Jun，CUI Fuyi，et al.Application of BP neural network at Yuqiao reservoir［J］.Journal of Zhejiang University（Science A：An International Applied Physics ＆ Engineering Journal），2007，8 （9）：1482－1487.

［11］LI Hong，PENG Tao.Prediction of concrete compression strength based on BP and PBF neural network theories［J］.Journal of Wuhan University of Technology，2009，31 （8）：33－36 （in Chinese）.［李红，彭涛.基于BP、RBF神经网络混凝土抗压强度预测 ［J］.武汉理工大学学报，2009，31 （8）：33－36.］