钢结构设计中稳定性分析

潘秋生

（山西师范大学，山西 临汾 041000）

钢结构设计中稳定性分析

潘秋生

（山西师范大学，山西 临汾 041000）

钢结构优于钢筋混凝土结构的特点是工程成本更低，抗震强度更高、空间更加节省。在高强度的钢材得到广泛应用，建筑施工技术取得更大发展，电子计算机技术得到普及应用的今天，钢结构体系具备了广泛推广应用的所有条件。在钢结构得到普及和发展的同时，也暴露出更多的设计方面的问题，其中一个突出的问题便是稳定性。

钢结构；设计；稳定性

1 钢结构稳定性的相关概念

1.1 稳定性的概念与分类

这里的稳定性问题指的是建筑结构在外界的扰动之下恢复至初始的平衡状态的能力。与稳定相对的是失稳，失稳指的是建筑结构或建筑构件在外界的扰动下从初始的平衡位置移动至另外一个平衡位置。失稳可分成三种类型，第一种类型是指具有平衡分岔的稳定问题，也称之为分支点失稳，这是指直杆、圆环和窄梁的轴心受到压力可能出现的分支点失稳现象。第二种类型指的是无平衡分岔的稳定问题，或称之为极值点失稳，极值点失稳现象在建筑结构中十分普遍，在建筑实际当中，常将极值点失稳变换成分支点失稳进行处理。第三种类型是跃越失稳，这种失稳类型不同于上述两种类型，跃越失稳是指在一种平衡状态受到破坏后直接进入到另外一种平衡状态。

1.2 钢结构稳定相关的影响因素

将钢结构稳定相关的影响因素划分为三种类型。

1.2.1 结构体系内的影响因素

主要包括结构不可缺少的支撑系统，例如钢柱间的支撑，再如钢屋架上弦水平支持与下弦水平支撑，还有垂直支撑等支持系统。

1.2.2 构件本身的影响因素

这是指构件的长度与截面的数值特性，其中包括平面内和平面外的两个方向，此外还有材料具有的强度性和应力特征。

1.2.3 随机性影响因素

在做结构分析时所应用的数学模型以及假设的条件，按照有限样本所总结出来的有关物理量及几何量这些都可能存在误差，造成稳定分析出现偏差。

1.3 钢结构稳定设计具有的特点

（1）关于轴心压杆的两种常用算法为临界压力求解法及折减系数法。

（2）由于杆件具有的稳定性涉及到钢结构的整体，所以应以整体结构来对各杆件稳定性进行分析。

（3）在钢结构的设计规范当中包含了一阶弹性分析法及二阶弹性分析法二种分析法，鉴于分析钢结构的稳定性时将涉及二阶效应，也即是结构及位移对于内力所产生出的影响。所以，在进行钢结构稳定性分析时在理论上宜采用二阶分析法。特别对于柔性结构，因为这种结构的侧移及竖向都承担较大的荷载。如今还存在三阶分析法，这种分析法针对的是大变形与大挠度的问题，此时的曲率与位移导数间无明显线性关系。

（4）弹性计算过程中无法运用迭加原理，原因是运用迭加原理要求建筑结构的变形要小，而弹性稳定计算通常无法满足该项条件。至于非弹性计算因无法满足这项条件，亦无法对迭加原理进行运用。

（5）由于稳定分析仅针对位移做判断，故稳定分析无须分析建筑结构具有的超静定的特性。

1.4 钢结构稳定设计应遵循的原则

依照钢结构在设计过程中暴露出来的问题，在钢结构设计当中应遵循以下原则：

1.4.1 在结构设计时应同时顾及整体稳定性与局部稳定性

在进行结构设计时应有必要的支撑结构，以确保平面结构不会产生失稳现象。如今大部分的钢结构均为依平面体系进行设计，这就需从结构整体上进行布置加以解决。设计平面桁架所组成的塔架时，应考虑到杆件的稳定性与横隔的设置存在的关系。

1.4.2 应用的计算简图应与结构计算简图保持一致

进行单层框架结构设计及进行多层框架结构设计时，习惯于以框架柱的稳定计算来替代对其进行的稳定分析。这个过程当中所应用到的柱计算的长度系数可经对框架整体的稳定性进行分析而得出，鉴于实际的框架存在多样性，出于简化计算的考虑需设定部分典型条件。而通常使用的计算方法一般只考虑到典型情况，造成了计算上出现误差。

1.4.3 结构计算与构造设计应保持一致

针对不同的节点间的连接应进行不同刚度与不同柔度的设置，设计桁架节点时要尽可能使杆件的偏心减到最小。但在涉及到稳定性时，在构造方面常出现与强度要求不相同的特殊要求。在处理梁的整体稳定性时，应不动铰支座以有效阻止出现位移现象，以及出现梁绕纵轴发生的扭转现象，应使其在平面之内自由转动以及在梁的一端截面之上产生翘曲，目的是使边界条件符合稳定性分析的要求。对相关基本概念的把握有助于深入了解稳定性设计存在的薄弱环节，掌握设计当中应注意哪些问题。钢结构理论研究在钢结构应用的普及和发展背景下也取得了很大成果，钢结构设计者应通过了解相关基本概念来强化稳定性分析的理论基础。

2 钢结构稳定性的分析方法

2.1 静力法

所谓静力法指的是静力平衡法，静力法是结构在出现微小变形之后，依据其现有受力条件构建起所需要的平衡微分方程，然后求解临界荷载。基本假设条件为：构件的假设条件为等截面的直杆；从始至终压力的作用都是沿构件原轴线传递的；涉及到的材料全部符合胡克定律；构件符合平截面的假定条件，也即是指构件变形前后平截面始终是平截面；构件变形程度微小，弯曲的曲率可以挠度函数之二阶导数来近似表达。

2.2 能量法

这种方法是对稳定承载力进行求解的近似分析方法，所运用的原理是能量守恒原理以及势能驻值原理。

2.2.1 能量守恒原理在求解临界荷载中的应用

依据能量守恒原理，体系处在平衡状态，体系之内的应变能等于外力所做的功。处于临界状态时的能量关系式是：其中，应变能增量为ΔU；外力功增量为ΔW指。

2.2.2 势能驻值原理求解临界荷载的应用

势能驻值原理内容：结构在外力作用下产生微小的位移改变时，结构具有的总势能不变，也即是，此时的结构仍处于一种平衡状态。数学表达式是：dΠ=dU-dW=0其中，虚位移所引起的结构内的应变能发生的改变值为dU，其始终呈正值；外力对虚位移所作的功为ΔW。

2.3 动力法

在平衡状态之下，对结构进行微小干扰使其体系产生振动，因此发生的结构变形同振动加速度都同作用在结构上的荷载存在关联。发生变化后的荷载小于稳定状态之下的极限荷载值时，加速度反向于变形方向，故干扰消失后的运动趋向静止，而结构的平衡状态处于稳定状态；反之，发生变化后的荷载大于稳定状态的极限荷载值时，加速度同向于变形方向，干扰消失后其运动依然呈发散状态，结构的平衡状态将处于不稳定的状态之中，而临界状态荷载为结构的屈曲荷载，当结构振动的频率等于零时，即可求解。

3 钢结构稳定性的计算方法

3.1 计算长度法

现行的GB50017-2002钢结构设计规范（简称为《规范》）计算结构当中的单个柱子稳定性运用的是计算长度系数法。该规范把框架划分成两种，一种是无支撑的纯框架，一种是有支撑的框架。运用一阶弹性分析法对内力进行计算，框架柱的计算长度系数μ可查表求得（依据《规范》5.3.3条），也可依据《高层民用建筑钢结构技术规程》中的近似公式（见第6.3.2条）进行计算。

3.1.1 在有侧移时

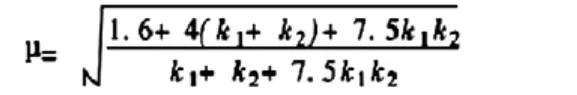
3.1.2 在无侧移时

这种方法的缺点是：实际的钢结构，其梁和柱均有弯矩与弯曲的存在，而处于非理想状态的无初弯曲构件，可通过查计算长度系数表，但只注意到与柱子相接连接的横梁所具有的约束作用，而结构的失稳仍表现为是整层甚至整个结构处于失稳状态，而非单个柱子处于失稳状态。并且利用软件进行结构设计确定柱子的计算长度还有一定难度。改进依据《规范》的5.3.6条：计算附以摇摆柱的框架（包括无支撑框架柱和弱支撑框架柱）长度系数时，要乘以增大系数η：

上式中 ，∑（Nf/Hf）是各框架的轴心压力设计值同柱子的高度比值之和；∑（N1/H1） 是摇摆柱的轴心压力设计值同柱子高度比值之和。依据相关规范（《门式刚架轻型房屋钢结构技术规程》之第 6.1.3条）：多跨刚架的中间柱出现摇摆柱状态时，进行边柱的计算长度系数要乘以增大系数η。

3.2 二阶分析法

式中的Qi是第i层楼重力荷载的设计值；ns是框架的总层数，在 时，取1；αγ是钢材强度的影响系数。在柱轴线压力设计值大于 时，应于其中央施加发水平力0.01N，目的是顾及P—Δ效应。P—Δ 效应起增大侧移的作用。P—Δ效应对于较多层数且侧向刚度较小的框架的影响作用明显，而对于一层框架和二层框架的具有影响不那么明显。应用此种分析方法做内力计算时，考虑到每层柱顶的假设水平力，应以几何长度做框架计算长度。

3.3 采用高等分析法进行整体设计

高等分析法的优点是计算时无须将框架拆卸成众多的横梁和柱，而是把框架看作一个整体结构，直接计算其承载力，计算只涉及框架的几何长度。

4 结语

从事钢结构的设计的人员应把握结构构件所具有的稳定性能，在设计过程中，应避免出现结构失稳现象，给设计工程带来不必要的风险损失，设计人员要对新结构的性能提前学习和认知，掌握新型结构知识，不断设计出稳定的钢结构作品。

[1]郑玉峰.钢结构稳定性设计探析[J].科技资讯，2011（08）.

[2]张涛,任前进.浅谈钢结构稳定性设计[J].中小企业管理与科技（上旬刊），2011（05）.

[3]孙菁丽.钢结构设计中稳定性分析探讨[J].中国新技术新产品，2010（08）.

TU391

A

1671-3362（2013）07-0020-02

潘秋生（1963-），山西临汾人，本科学历，副教授。研究方向：机械工艺。