压力表计量基础知识讲座

戴孝华/上海市计量测试技术研究院

第三讲 弹性元件特性及其在压力表中的应用

1 弹性元件及其使用的材料

1.1 弹性元件的种类

压力表使用的弹性元件目前有如下四种形式：

弹簧管：分为C形弹簧管、螺旋管、盘旋管。

膜 片：分为平面膜片、波纹膜片（可按波纹的截面形状又分若干种）。

膜 盒：分为单膜盒、膜盒组（两膜盒、三膜盒等）。

波纹管：分为无缝波纹管、焊接波纹管（可按波纹的截面形状又分若干种）。

1.2 弹性元件使用的材料

锡磷青铜：牌号有QSn6.5-0.1，QSn4-0.3。铍青铜：牌号有 QBe2。

高强度、高弹性合金钢：牌号有 50GrVA。

恒弹性合金钢：牌号有 3J53等。

不锈钢：牌号有 1Gr18Ni9Ti， 0Gr18Ni9 (SUS304)，0Gr17NI12MO2(SUS316)等。

2 弹性元件的基本特性

弹性元件的基本特性包括：弹性特性、刚度、灵敏度、弹性后效、弹性迟滞、弹性滞后、疲劳极限、环境温度影响等内容。

2.1 弹性特性

从低碳钢的“应力－应变”（σ-ε）曲线为例（图1），说明材料的弹性特性。

2.1.1 线性弹性阶段（Oa段）：在拉伸的初始阶段，应力σ与应变ε的关系为直线关系，即在Oa这一阶段内，σ与ε成正比，关系式为

式中：E － 为与材料有关的比例常数，通常称为弹性模量。

式（1），即为著名的材料拉伸和压缩试验的虎克定律。

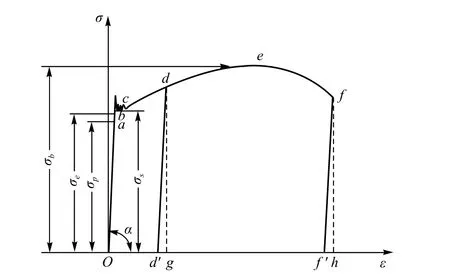
图1 低碳钢材料的“应力-应变”曲线

直线Oa的最高点a所对应的应力，用σp表示，通常称为比例极限。

由此可见，当应力低于比例极限时，应力与应变成正比，材料服从虎克定律。超过比例极限后，从a点到b点，σ与ε之间的关系不再是直线，但变形仍然是弹性的，即消除拉力后变形将完全消失。所以，b点所对应的应力是材料出现弹性变形的极限值，称为弹性极限，用σe表示。在σ-ε曲线上，a、b两点非常接近，所以，工程上对弹性极限和比例极限并不严格区分，因而可以认为，应力低于弹性极限时，应力与应变成正比，材料仍然服从虎克定律。

在应力大于弹性极限后，如再消除拉力，则试件变形的一部分随之消失，但还遗留下一部分不能恢复的变形，前者称为弹性变形，后者称为塑性变形。

2.1.2 屈服阶段（bc段）：当应力超过b点、并增加到某一数值时，应变有非常明显的增加，而应力却是先下降，然后在很小的范围内波动，在σ-ε曲线上出现接近水平线的小锯齿形的线段。这种应力先是下降，然后就基本保持不变，而应变又显著增加的现象，称为屈服或流动。其极限称为屈服极限或流动极限，用σs来表示。当材料屈服阶段试验曲线最低点的应力处于屈服阶段时，将引起显著的塑性变形，通常零件的塑性变形将导致机器不能正常工作而损坏，所以，屈服极限σs是衡量材料强度的重要指标。

2.1.3 强化阶段（ce段）：超过屈服阶段后，材料又恢复了抵抗变形的能力，要使变形增加，必须增加应力，这种现象称为材料的强化。在强化阶段中的最高点e所对应的应力，就是材料能承受的最大应力，称为强度极限，用σb来表示。

2.1.4 局部变形阶段（e f段）：当应力超过σb后，在试件的某一局部范围内，横向尺寸突然急剧缩小，形成“颈缩”现象（图2），当应力降低到f点时，试件被拉断（图3）。所以，强度极限σb是衡量材料强度的又一重要指标。

图2 材料颈缩现象

图3 材料被拉断现象

2.2 刚度

使弹性元件产生单位位移所需要的载荷（可以是力或压力或力矩）。刚度一般用符号kp表示。

对于线性的弹性特性元件，刚度可用下式表示：

式中： p — 产生单位位移的载荷；

W — 单位位移

2.3 灵敏度

弹性元件承受单位载荷时所产生的位移（可以是线位移或角位移）。灵敏度一般用符号s表示。灵敏度可用下式表示：

式中的符号意义与上面公式相同。

由式（3）可知：灵敏度是刚度的倒数。刚度和灵敏度是弹性元件同一特性的两种表现形式，对于位移式仪表，多采用灵敏度来衡量仪表的特性，通常，压力表使用灵敏度而不用刚度。

2.4 弹性后效

当弹性元件承受的载荷取消后，弹性元件不能立即恢复到原来的形状和尺寸，而是要经过一段时间以后，弹性元件才能恢复到原来的形状和尺寸，这种现象称为弹性后效（图4）。

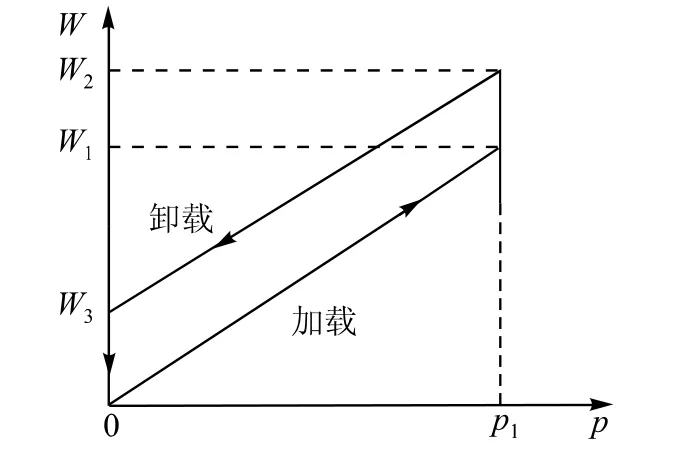
图4 弹性后效曲线

从图4可以看出：当载荷由起始0点加载到压力p1时，对应的变形位置（位移）为W1，由于存在屈服现象，继续变形而稳定在W2位置。当载荷由p1卸载到0点时，变形由位置W2回到位置W3，而没有直接回到0点，经过若干时间后，变形恢复到0点，形成了变形（位移）在恢复过程的后来效应，故而称为弹性后效。

2.5 弹性迟滞

当弹性元件的加载曲线和卸载曲线不重合时，产生了在同一载荷下变形（位移）不一致的现象，这种现象称为弹性迟滞。

从图5可以看出：加载时的变形（位移）为W1，卸载时的变形（位移）为W2，故，

ΔW = W2- W1，即为弹性迟滞。

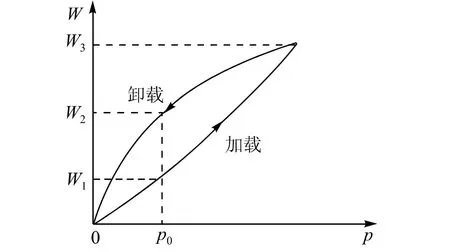
图5 弹性迟滞曲线

2.6 弹性滞后

请注意：实际上，弹性后效和弹性迟滞是同时发生和存在的，通常两者叠加在一起而无法分开，所以，一般情况下统称为弹性滞后。弹性滞后给压力表的计量性能造成不利的影响，所以，在设计和制造弹性元件时，应尽量减少弹性滞后的影响。为此，在压力表的计量性能中，对回程误差（滞后误差）提出了限制要求，就是这个道理。

2.7 环境温度影响

环境温度的变化，会引起材料弹性模量E的变化，通常使用弹性模量的温度系数来表示弹性模量随温度的变化，即用下式表示：

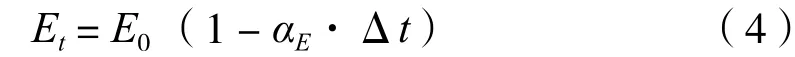
式中：Et— 温度（t）变化后的弹性模量；

E0— 温度（t0）变化前的弹性模量；

Δt— 温度变化量，Δt = t - t0；

αE— 弹性模量的温度系数

由式（4）可知：温度系数αE越大，则Et越大。所以，选择弹性元件时，要选择弹性模量温度系数小的材料。常用材料弹性模量的温度系数，可见表1。

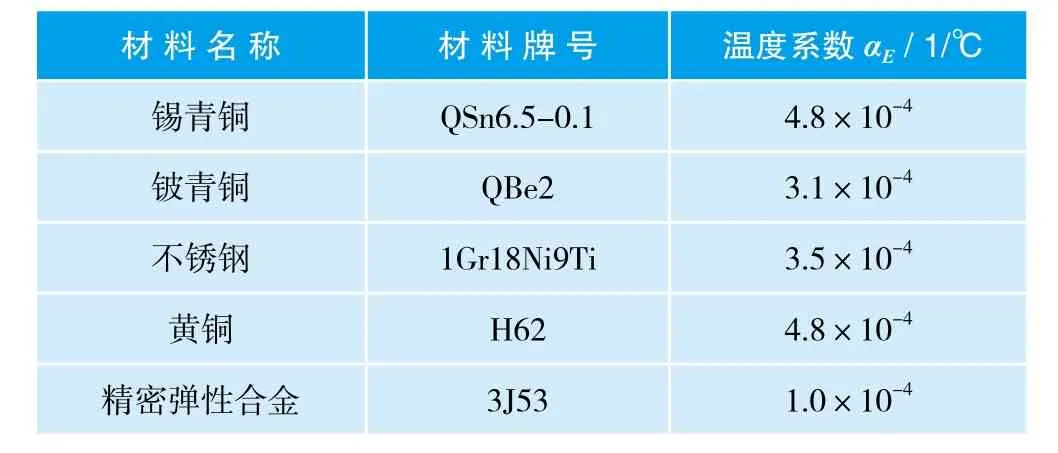
表1 常用材料弹性模量的温度系数

2.8 疲劳极限

当弹性元件承受交变应力（或载荷）反复作用而导致破坏的现象，称为疲劳破坏。不产生疲劳破坏的极限值，称为疲劳极限。

为了便于考核和量度，通常以弹性元件能承受106～ 107次交变载荷而作为疲劳极限的考核指标。这个疲劳极限就是压力表在型式试验或样机试验中要求做交变试验的依据。

3 弹性元件基本特性在弹簧管设计和使用中的应用

3.1 弹簧管管端位移量与承受压力的关系

弹簧管在压力作用下，管端位移量在一定的范围内与压力之间是成直线、正比例的关系，如图6所示。

由图6可见：随着压力的增加，管端位移W成正比例的增加，对应A点的压力pb，即为弹簧管的比例极限，超过A点就不成正比例关系，直线开始弯曲。所以，在设计弹簧管时，通常总希望设计制造的弹簧管在需要的压力下具有足够的管端位移量，以获得较高的灵敏度。

图6 管端位移与压力大小关系曲线

根据实验结果可以知道，影响弹簧管管端位移量的因素有如下几种：

3.1.1 弹簧管的轴径比a/b（长轴/短轴之比），管端位移W随a/b增大而增大，如图7（a）所示。

3.1.2 弹簧管的曲率半径R，管端位移W随R的增大而增大，如图7（b）所示。

3.1.3 弹簧管的壁厚h，管端位移随h的增大而增大，如图7（c）所示。

3.2 安全系数

前面介绍过，弹簧管管端位移与压力成正比例的关系，这是有条件的（不是随意能达到的），就是压力表的工作压力不能超过最大压力pmax，如果超过最大压力pmax，正比例的关系就被破坏。所以，图6中的A点，通常称为弹簧管的比例极限，也就是说，正常使用的弹簧管所能承受的工作压力不能超过A点，即比例极限，很明显，超过A点，就会产生非弹性变形。但是，即使做到这种程度，还不能满足要求，因为，弹簧管始终存在着弹性后效和弹性迟滞的影响。为了保证弹簧管的实用性，相对比例极限而言，还要给弹簧管一个安全系数，即，弹簧管的比例极限与最大工作压力之比，称为弹簧管的安全系数，可用下式表示：

式中：kb— 安全系数；

pb— 比例极限；

pmax— 最大工作压力

图7 管端位移与影响因素关系曲线

比例极限一般可以用测量方法确定，压力表的安全系数一般要求为1.5或2。

3.3 影响比例极限的因素

从式（5）又可以知道：在一定的压力下，要提高安全系数，就必须提高比例极限。根据实验结果可以知道，影响比例极限的因素有如下几种：

3.3.1 弹簧管轴径比a/b，比例极限随着a/b的增大而减小，如图8（a）所示。

3.3.2 弹簧管的曲率半径R，比例极限随着R的增大而减小，如图8（b）所示。

3.3.3 弹簧管的壁厚h，比例极限随着h的增大而增大，如图8（c）所示。

3.3.4 弹簧管的强度极限σb，比例极限随着σb的增大而增大，如图8（d）所示。

根据以上四项影响因素，要想提高比例极限，可采用减小轴径比、减小曲率半径、增加壁厚、选用强度极限高的材料等办法来达到。

3.4 灵敏度

影响弹簧管灵敏度的因素有如下几种：

3.4.1 弹簧管的轴径比a/b，灵敏度随着a/b的增大而提高，如图9（a）所示。

3.4.2 弹簧管的曲率半径R，灵敏度随着R的增大而提高，如图9（b）所示。

3.4.3 弹簧管的壁厚h，灵敏度随着h的增大而降低。如图9（c）所示。

灵敏度的大小可以帮助设计人员选择传动机构的传动比和确定分度盘的标度。

图8 比例极限与影响因素关系曲线

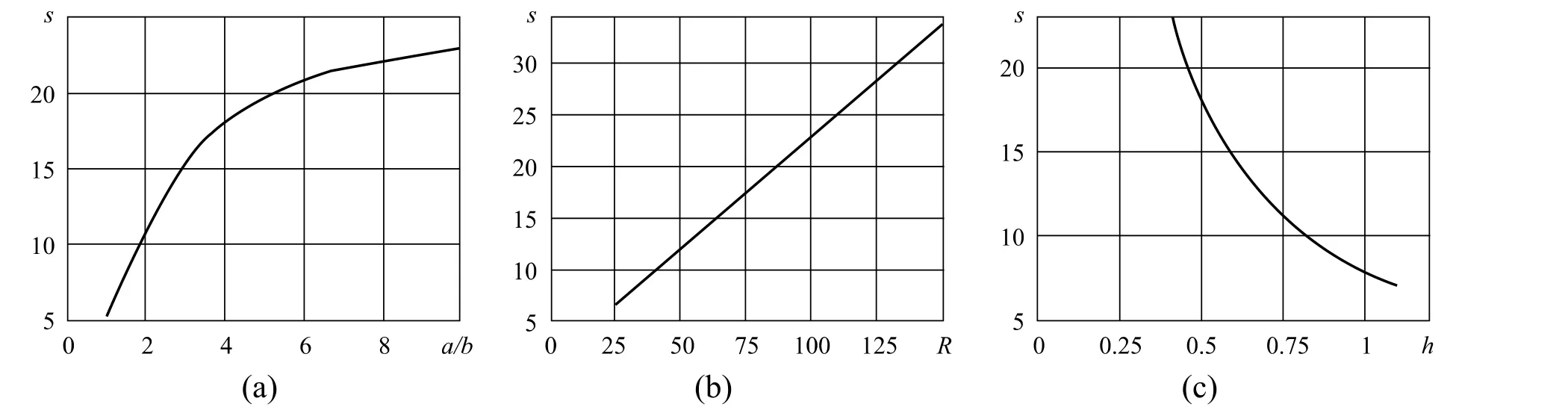
图9 灵敏度与影响因素关系曲线