软硬交接地层导向孔钻进轨迹预测
彭 旭,胡文礼,艾志久,胡 坤
(西南石油大学 机电工程学院,成都610500)
水平定向穿越施工方法广泛应用于地下管道铺设工程,导向孔钻进为水平定向穿越施工的第1阶段。在导向孔钻进过程中,关于软硬交接地层对钻进轨迹的影响早在20世纪50年代初便有人开始研究[1]。当前,对于钻头与软硬交接地层相互作用规律,以及软硬交接地层对钻进轨迹的影响,主要利用工程公式进行数学推导来预测[2];同时,导向孔钻井钻头为三牙轮钻头,由于钻头复杂性,部分学者对结构进行简化计算,因此使用范围有一定局限性。
随着有限元分析理论的成熟,有限元仿真软件Abaqus在处理岩石破碎、动态接触等非线性问题上,具有强大的运算求解功能[3]。因此,本文采用Abaqus软件对软硬交接地层导向孔钻进进行模拟,得到软硬交接地层中导向孔轨迹变化情况。
1 钻头破岩运动学模型
在研究三牙轮运动学时,作如下基本假设[4]:①不考虑钻头牙齿的形状及复合运动;②井底形状为光滑平面或锥面;③岩石破碎与牙齿吃入深度的某次方成正比;④各接触齿作用力相同。
三牙轮钻头在地层钻进过程中的运动主要分为牙齿对地层岩土的横向刮凿破碎和钻头的纵向振动[5]。对于牙轮钻头破岩,存在牙轮绕钻头中心线旋转与牙轮绕自身轴线旋转的复合运动,同时牙轮随钻头本体纵向移动。因此,牙轮运动包括转动和纵向移动,牙轮自转当作相对运动,牙轮上任何一点的运动均为复合运动。牙轮上任意一点速度方程如下:
牙轮径向分速度为

由式(1)可知:牙轮上任意一点的径向分速度受该点在牙轮上的位置、牙轮的自转角速度、钻头的几何结构参数以及牙轮位置的影响,与钻头本体的纵向移动速度和旋转速度无关。
牙轮切向分速度为

由式(2)可见:牙轮上任意一点的切向速度取决于牙轮自转角速度和钻头角速度;当牙轮自转角速度和钻头角速度大小相等时,该点处于滚动状态;当钻头转速一定时,牙轮转速越小,则切向速度越大,牙齿向前滑移速度越大;当切向速度出现负值时,牙齿向后滑移。
牙轮纵向分速度为
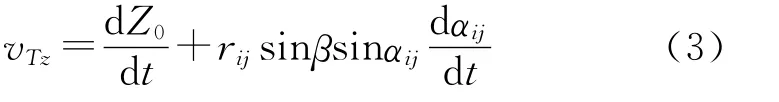
式中:C、β、S 为钻头结构参数;rij、αij、hij为牙轮位置参数;为钻头的运动参数;为牙轮运动参数。
根据速度合成原理,可计算得到牙轮绝对速度。
2 有限元分析
2.1 建立几何模型
运用Solidworks建立钻杆、钻头与地层相互作用模型。钻头采用三牙轮钻头,为了减少建模与仿真计算工作量,将钻头简化,忽略钻头次要结构。由于实际工程中三牙轮钻头在钻进过程中遇到软硬交接地层,因此软硬交接地层模型中有一部分成型孔,成型孔不参与仿真计算,假设成型孔内壁光滑。钻头与地层相互作用模型如图1所示。牙轮钻头由软地层经过软硬交接面进入硬地层。
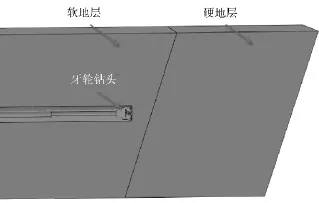
图1 钻头与地层相互作用模型
2.2 定义材料
钻头与地层相互作用为非线性动力学过程,软地层材料为固体粘土,硬地层材料采用砂岩,地层本构模型采用Drucker-Prager模型。Drucker-Prager模型是最早提出的适用于岩土类材料的弹塑性本构模型,其最大优点是考虑了岩土类材料的剪胀性或扩容性,在主应力空间的屈服面为光滑圆锥,表述极其简单且数值计算效率很高,在实际有限元计算中应用较广泛[6]。
钻头与钻杆为钢材料,密度为7 800kg/m3。软地层与硬地层参数如表1所示。

表1 地层参数
2.3 模型单元类型与网格划分
导向孔钻进过程中,钻杆、钻头与地层相互作用为动态非线性接触,采用动态显式求解方法进行求解[7-8],可提高求解速度。钻杆、钻头与地层均采用显式3D应力缩减积分单元,该单元在求解地层岩土失效与岩土去除等高度非线性问题上优势明显[9-10],采用增强沙漏控制方式控制单元变形内能。
钻杆、钻头以及地层模型网格划分如图2~3所示。钻头牙轮与地层接触较为复杂,因此在主要接触区域进行适当网格细化,提高求解精度[11]。

图2 钻杆和钻头网格划分

图3 地层网格划分
2.4 定义接触与边界条件
在导向孔钻进过程中,三牙轮钻头表面与地层间接触为高度非线性动态接触。在钻头旋转钻进过程中,钻头表面与地层表面接触不断发生变化,因此采用有摩擦的通用接触算法[5],可简便定义钻头与地层间复杂的接触关系。
将地层四周采用完全固定约束,计算模型整体尺寸为钻头与地层作用面积尺寸的10倍,以此忽略边界固定对仿真分析的影响,设定地层倾角70°,钻进位移为1.2m。
3 仿真结果分析
水平定向穿越施工,三牙轮钻头软硬交接地层钻进有3个状态:钻头在软地层中钻进;钻头通过软硬交接地层;钻头在硬地层中钻进。
3.1 钻头岩土破碎
软地层在受到三牙轮钻头钻进压力及旋转剪切作用下,首先产生压缩弹性变形,随后出现岩土移除,如图4所示。仿真设置中软土为均质粘土,不考虑地层岩土缝隙。
3.2 牙轮钻头位移变化
在软硬交接地层进行水平定向穿越导向孔施工时,地层与牙轮钻头进行随机性的动态接触。当牙轮与地层产生接触后则产生摩擦力、冲击力,导致钻头振动。三牙轮钻头由软地层进入硬地层,必然会产生较大的横向摆动与上下振动。

图4 软地层钻进(剖视图)
牙轮钻头前进过程的ALLAE曲线如图5所示。该曲线代表伪应变能,主要包括粘性和弹性2项,然而由于粘性项通常占主要的地位,因此大部分转化为伪应变能的能量是不可恢复的。伪应变能是控制沙漏变形所耗散的主要能量,如果伪应变能过高,说明过多的应变能被用来控制沙漏变形,这时则必须对网格进行细化或者对网格进行其他的修改,以减少过多的伪应变能[6]。本模型中伪应变能突变主要在钻头进入软土层以及牙轮钻头穿越软硬交接地层界面时。由图5可知:地层硬度越大,钻头进入地层的伪应变能增幅越大。

图5 伪应变能ALLAE曲线
当钻进速度v=0.004m/s时,钻头横向偏移与纵向偏移如图6所示。

图6 钻头轨迹偏移曲线
由图6可知:三牙轮钻头在软硬交接地层钻进过程中,发生纵向偏移,横向为钻头规律性振动。同时根据钻头轨迹纵向偏移可知:钻头在软地层中钻进时,振幅较小,而在硬地层中钻进是振幅较大;由于岩土硬度增加,钻头牙齿在对岩土刮凿破碎过程中需要的转矩增大,岩土破碎瞬间产生惯性力较大,因此钻头振幅增大。
图7为钻进速度v=0.003m/s与v=0.004 m/s时钻头钻进轨迹对比情况。由图7可知:钻进速度越大,钻头与地层不规则接触频率越高,旋转加速度以及钻进速度较大,钻头横向振动幅度越大;钻进速度越大则钻进轨迹纵向偏移越大。
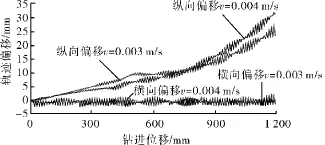
图7 钻头轨迹偏移对比曲线
4 结论
1) 伪应变能突变主要在钻头进入软土层以及牙轮钻头穿越软硬交接地层界面时,地层硬度越大,钻头进入地层的伪应变能增幅越大。
2) 三牙轮钻头在软硬交接地层钻进过程中,发生纵向偏移,同时钻头发生振动,地层硬度越大,钻头振幅越大。
3) 钻进速度越大则钻进轨迹纵向偏移越大。
4) 本文的研究结果对提高软硬交接地层中三牙轮钻头钻进轨迹预测准确性具有重要意义。
[1]Lubinski A,Woods H B.Factors Affecting the Angle of Inclination and Dog-legging in Rotary Bore-Holes[J].Drilling and Production Practice,1953,23(7):222-250.
[2]周祖辉.钻软硬交错地层时钻头弯矩及转角的计算方法[J].石油大学学报:自然科学 版,1990,14(2):16-18.
[3]邵增兀,江礼军.使用ABAQUS软件进行牙轮钻头破岩过程模拟[C]//ABAQUS软件2003年度用户论文集,2003.
[4]马凤清,唐 波,冯光通,等,三牙轮钻头与地层相互作用动力学数值模拟[J].石油矿场机械,2012,41(9):5-9.
[5]杨春雷.钻头齿圈复合运动破岩系统仿真研究[D].成都:西南石油大学,2006.
[6]赵明阶.岩石力学[M].北京:人民交通出版社,2011.
[7]伍开松,赵 云,柳庆仁,等.高压射孔测试管柱力学行为仿真[J].石油矿场机械,2011,40(5):74-76.
[8]刘 林,陈和平,李永革,等.水平井分段压裂封隔器研制与封隔性能分析[J].石油矿场机械,2012,41(5):86-88.
[9]温纪宏,陈国明,畅元江,等.隔水导管螺纹接头连接性能研究[J].石油矿场机械,2012,41(12):17-20.
[10]Abaqus Documentation.ABAQUS Analysis User’s Manual[K].2012.
[11]康永田,田红平,罗晓兰,等.水下采油树内部输油管应力分析[J].石油矿场机械,2011,40(4):33-36.

