基于遗传神经网络的黑龙江浅表地层水分预测

许秀英，黄操军，杨秋梦

（黑龙江八一农垦大学，黑龙江 大庆163319）

田间土壤水分预测是水资源管理的基础内容，对农田灌溉排水具有重要的指导意义，主要研究土壤特性、作物根系发展、降水、灌溉、蒸散、气象等因子的变化及相互作用对土壤墒情变化的影响。神经网络法具有良好的非线性映射能力，对被建对象的经验要求较少，常被用于土壤墒情预测，且多采用BP神经网络模型。但BP模型在较大搜索空间内易陷入局部极值点，且输入参数的选取对模型成功与否具有重要影响，输入参数少，预测精度降低；参数过多，容易导致模型计算无法收敛或收敛时间过长，影响了BP神经网络的泛化能力。本文针对神经网络存在的缺点，采用具有全局搜索与优化能力的遗传算法与BP神经网络相结合的方式，以黑龙江垦区广泛种植的农作物——大豆为研究对象，根据根系分布对土壤水分吸收的影响划分土层，基于植物蒸散发过程受气象因子影响较明显的特点，选取5个气象因子引入遗传神经网络（GA—BP）土壤水分预测模型，实现遗传神经网络对土壤水分的预测。

1 作物根系分布对土壤水分吸收的影响

土壤含水量、根系密度和根系吸水活力是作物根系对土壤水分吸收的共性特点。当土壤水分含量达到一定水平时，根系吸水不受含水量影响，只受大气决定的蒸散力与根系分布密度的影响；根系分布合理时，根系吸水量与吸水速度与土壤的垂直水分含量有关。作物根系分布具有一定的规律性，如大豆根系在0—45cm土层的分布占总根系的90%左右［1－2］，已有研究表明，大豆、玉米和谷子等作物的根系绝大多数主要分布于0—45cm 这一土层范围内［3－7］，0—45cm土层亦是旱田作物的主要吸水区。因而本文选取黑龙江寒地大豆种植中0—50cm土层范围的土壤含水量开展研究与预测，建立土壤水分预测模型。

2 遗传神经网络预测模型的网络结构和参数的确定

2.1 遗传神经网络设计

将遗传算法与神经网络相结合，利用遗传算法的全局寻优能力，在大范围内对BP神经网络的权值和阈值进行搜索寻优，将搜索到的全局最优解赋予BP网络，再利用BP网络较好的局部搜索能力进行精确搜索，从而达到获得最优权和阈值的目的。

2.2 遗传神经网络预测算法

2.2.1 BP网络原理 BP网络是前馈多层神经网络，由干神经元以一定的连接方式组成，可以模拟不能用明确的数学公式表达的非线性函数关系，该函数关系可通过节点间连接权值和节点阈值的综合运算来实现［4］。训练集包括 M 个样本模式对（Xk，Yk）。对第p个训练样本（p＝1，2，…，M），单元j的输入总和（即激活函数）记为apj，输出权值记为Opj权值记Wpj，则：

式中：dpj——对第p个输入模式输出单元j的期望输出，δ学习规则的实质是利用梯度最速下降法，使权值沿误差的负梯度方向改变。设隐含层与输出层、输入层与隐含层的连接权值分别为ωkj和vji，则其调整值为：

神经网络的输入节点数确定为：10个。选取地表0—10，10—20，20—30，30—40，40—50cm共5个层面的土壤水分数据和降雨量（R6）、蒸发量（L0）、气温（W0）、空气湿度（U0）、日照时数（S2）5个气象因子作为预测模型的输入因子；隐含层节点为22个［6］；输出节点为一个，即农作物根系生长层的土壤水分变化情况。

2.2.2 遗传优化 采用遗传算法对神经网络连接权值进行优化，使遗传算法能很快确定全局最优解存在的区域，在该区域内再利用BP算法较强的局部搜索能力，较快完成网络的训练优化，其过程如下：

（1）编码与种群初始化。采用十进制编码方式，按神经网络生成初始权重的常规办法来生成网络的权重，任一组完整的网络权重xi＝｛w1，w2，b1，b2｝（i＝1，2，…，m）相当于一个染色体，由神经网络的权、阈值组成，这样的染色体共有m个，即种群规模为m。其中w1为输入层与隐层之间的权重值，w2为隐层与输出层之间的权重值，b1为隐层阈值，b2为输出层阈值。染色体长度计算公式为：

式中：S1——隐层结点数量；S2——输出数量；r——输入数量，遗传操作在这样的染色体群中进行。

（2）GA在进化搜索过程中是以适应度函数为依据的，故适应度函数的选择直接影响到GA的收敛速度以及能否找到最优解。根据适应度函数值的大小对全部个体进行评价，本文选用的适应度函数为：

式中：yk——网络的实际输出，对应预测含量；tk——网络的标准输出，对应训练样本元素的真实含量；n——训练集样本数。计算出适应值后，将其按照从大到小的方式进行排列。

（3）选择算子，依据比例法选择适应度大的染色体，第i个染色体的适应值为F（i），则其被选中的概率为：

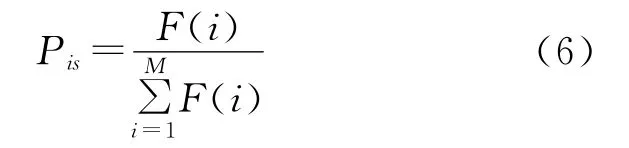
式中：Pis——选择概率；M——种群大小。

（4）选用算术交叉方式，其交叉概率Pc为0.6。

（5）变异运算可产生初始种群中不被包含的基因，或找回选择过程丢失的基因，为种群提供新的内容。以变异概率Pm＝0.08进行变异操作。变异量X＝x1，x2，x3，…，xm，其变异点xm的取值范围为［a，b］，变异点的新基因为：

式中，r∈［0，1］内的符合均匀概率分布的随机数，t——当前进化代数；T——终止代数；b——系统形状参数。

重复以上步骤，当网络误差或进化代数满足条件时结束遗传算法。遗传寻优完成后，选择最优权值和阈值、输入样本与输出样本输入BP网络模型，对网络进行训练。其最大训练次数为5 000，最大允许误差设定为0.001。

3 研究区概况与研究方法

影响土壤含水量的主要因素包括土壤内部富含根系的吸水情况与外部气象因子变化以及人工干预。因预测模型主要用于指导人工干预措施，所以建立模型期间忽略人工干扰的影响。输入变量为气象因子，输出变量为土壤含水量。本文对黑龙江红星农场的大豆作物进行土壤含水量的预报研究。红星农场位于黑 龙 江 省 北 安 市，北 纬 48°02′—48°17′，东 经126°47′—127°15′，属中温带湿润大陆性季风气候，是国家高油大豆优势产业带规划的松嫩平原优势区，多年平均气温0.8℃，≥10℃的有效积温2 254.5℃，无霜期115d，多年平均降水量553mm，年平均日照2 700h以上。地下水根据埋藏情况有3种类型：上层潜水、潜水和承压水，潜水距地表近，直接受大气降水和地表水的补给，含水层在1～3m，潜水深度为5～20m，承压水分布于全市境内，200m深共有5层承压水层。土壤毛管上升水最大可达5m，地下水位能够补充一部分土壤水分，土壤蒸发量较大。降水量的多少直接影响土壤水分的含量和时空变化特征，雨季土壤水分的动态变化与降雨量和土壤蒸发量密切相关，东北农田黑土的蒸发量随土壤含水量的增加而增大［8］。影响土壤蒸发量的主要气象因素为温度、日照时数和空气湿度，因而选取对土壤含水量影响显著的5个气象因子：温度、相对湿度、日照时数、降雨量和蒸发量，及2007—2008年每年4月—10月测得的0—10，10—20，20—30，30—40，40—50cm共5个土层的含水量数据作为网络训练样本数据，选取2009年4月—10月之间测得的土壤水分数据和相应的气象数据，按模型数据需求输入预测模型。得到的相应输出为指定层面的指定日期的土壤水分数据。红星农场每年4—10月的8日、18日、28日上报土壤水分数据。选取2007—2009年上报的819组土壤水分数据作为实验数据，其中2007年、2008年4—10月共546组数据的训练样本集，2009年273组数据作为测试样本集。输入样本数据X中包括：10—50cm的5个层面的土壤水分数据和5个气象因子数据R6，L0，W0，U0和S2；输出样本数据Y 为指定预测模型所对应的特定层面，按时间序列排列指定日期土壤水分数据。对输入、输出的样本数据应用premnmx（）函数进行归一化处理。按照递推关系输入网络，从而完成遗传神经网络预测模型的训练、建模过程。

4 土壤水分预测结果

大豆各生育期根的生长与分布形式不同，因季节更替等原因，各阶段对土壤水分的生理需求、吸收亦有所不同，根据不同的生长阶段建立3种土壤水分预测模型［9－12］，分别为0—15cm 土层（模型 A），10—30 cm土层（模型B），30—45cm土层（模型C），对黑龙江垦区红星农场大豆田间土壤水分进行预测。3种遗传神经网络模型参数设置和实现过程相同，只是预测的时间和预测土壤层面不同。

（1）模型A的预测结果。模型A适用于4月和5月的土壤水分预测。红星农场2009年在4月下旬进行大豆播种，播种深度在距地表5cm左右，发芽与出苗期阶段约在5月末完成，在此期间大豆根系分布主要集中于0—15cm土层范围内，因而，在该阶段选取地表10cm这一层面建立相应的土壤水分预测模型A并进行墒情预测。用训练好的模型A对2009年4月18日至5月28日的土壤水分进行预测，结果如表1所示。

表1 模型A对土壤水分的预测结果 %

从预测结果可以看出，模型A对大豆地播种前期、播种期直至出苗期有较好的预测精度，其土壤体积含水量的平均预测精度约为0.80%，能够满足农业生产实际需要，具有较高的预测精度及可靠性。

（2）模型B的预测结果。模型B适用于6月的土壤水分预测。此期间为大豆幼苗期，具有抗旱能力强的特点，大豆根系主要分布于于10—30cm这一土层范围内。这一阶段若土壤水分含量过高，易导致大豆根系发育不良。选取距地表20cm这一层面进行土壤水分研究，并建立相应的土壤水分预测模型B。用训练好的模型B对2009年6月8日至6月28日的土壤水分进行预测，结果如表2所示。

表2 模型B对土壤水分的预测结果 %

预测结果表明，模型B对大豆幼苗期土壤含水量的预测精度不高，其土壤体积含水量的平均预测精度为3.64%，因2009年6月份降雨量比较大，气候变化比较剧烈，对预测结果的影响较大。但是在天气多变的情况下，要想获得较高的预测精度是极其不易的，虽然模型B的预测精度不是很高，但也基本能满足实际农业生产需要。

（3）模型C的预测结果。模型C适用于7—9月的土壤墒情预测。此阶段为大豆开花至成熟期，具体包括开花—结荚、结荚—鼓豆、鼓豆—成熟3个生育阶段，各阶段需水量基本相当，吸水总量占全生育期的75%左右，是对水分需求最多的时期，在此期间大豆的根系主要在15—45cm这一土层范围内生长发育。选取距地表30cm处这一层面进行土壤水分研究，并建立相应的土壤水分预测模型C。用训练好的模型C对2009年7月8日至9月28日的土壤水分进行预测，结果如表3所示。

表3 模型C对土壤水分的预测结果 %

模型C的预测时期是大豆乃至小麦、玉米等其它农作物生长最重要的时期，这一时期农作物的吸水量大、生长迅速，农业从业人员必须熟知田间的具体情况，以便采取相应的农业生产措施，保证农作物的健康生长、促进农业丰产丰收。通过模型C对土壤水分的预测结果可知，模型C对该时期的土壤体积含水量的预测精度为1.97%，能很好地满足农业生产需求，为农业生产活动提供有力的参考。

5 结论

提出了一种基于GA－BP神经网络的土壤水分预测算法，该算法首先建立一个BP神经网络，并采用遗传算法对BP网络的节点权值进行优化，获取一个最优权值作为BP网络的初始权值，完成BP网络训练后，以5个气象因素及5个地层实测水分含量作为网络的输入，3个不同土层分别作为输出，经实测数据验证：GA－BP算法结合了遗传算法全局搜索和BP网络局部精确搜索的优点，进行土壤墒情预报，具有收敛速度快，准确率高的优点。

利用该法进行土壤墒情预测，能为科学灌溉决策管理提供依据。尽管文中建立的GA－BP混合模型对土壤墒情的预报取得了满意的效果，但由于土壤墒情的变化是一个复杂的过程，影响因素较多，同时，本文并没有根据降雨年型进行分类预测，本文建立的预测模型虽然对同类作物、同类降雨年型具有一定的参考意义，但是对于不同降雨年型，模型应用受限，因此在实践中还需改模型进行不断的完善和提高。

［1］ 张英善.作物根系与土壤水利用［M］.北京：气象出版社，1999.

［2］ 曹敏建.耕作学［M］.北京：中国农业出版社，2002.

［3］ Bohm W.Method of Sudying Root Systems［M］.New York：Springer Berlin Heilberg，1979.

［4］ 万玉琼，梁俊有.基于遗传算法改进BP网络的灾害预测模型研究［J］.中国水运，2008，8（4）：255－257.

［5］ 王振龙，高建峰.实用土壤墒情监测预报技术［M］.北京：中国水利水电出版社，2006.

［6］ 李彩霞，陈晓飞，韩国松.沈阳地区作物需水量的预测研究［J］.中国农村水利水电，2007（5）：61－67.

［7］ 崔丽洁，徐宝林.吉林省中西部地区土壤墒情实验研究［J］.吉林水利，2003（1）：14－15.

［8］ 徐庆华，刘勇，马履一，等.东北农田黑土蒸发量与土壤水分及气象因子的关系［J］.东北林业大学学报，2009，37（11）：82－84.

［9］ 田芳明，周志胜，黄操军.BP神经网络在土壤水分预测中的应用［J］.电子测试，2009（10）：14－16.

［10］ Huang Caojun，Li Lin，Ren Shouhua，et al.Research of soil moisture content forecast model based on genetic algorithm BP neural network［C］∥Computer and Computing Technologies in AgricultureⅣ.partII，China，Springer，2010（10）：309－316.

［11］ 邢贞相.遗传算法与BP模型的改进及其在水资源工程中的应用［D］.哈尔滨：东北农业大学，2004.

［12］ 孙敬.基于遗传神经网络的空调房间送风量预测研究［D］.南京：南京工业大学，2006.