近地震波的小波相对能量分布特征分析①

许康生，李 英，李秋红

（中国地震局兰州地震研究所，甘肃 兰州 730000 ）

0 引言

地震波携带着丰富的震源信息和路径介质信息，人们希望通过对地震信号的分析获取所关注的信息。对地震信号处理最经典的方法是傅里叶变换，但傅里叶变换是纯频域的分析方法，处理时丢失了时间信息。又因为傅里叶变换严格要求系统的线性、信号的平稳性，对于非平稳信号表现出很大局限性。后来发展的短时傅里叶变换（STFT），受窗函数的制约，不能在时间域和频率域同事得到很好的分辨率。小波变换由于具有多分辨率的特征，其时间窗和频率窗随信号的具体形态可以动态调整，在时域和频域表征局部信息的能力得到加强。本文期望通过对地震信号的多分辨率分解，展现地震波在频域和时域的动态特征和规律。对近地震的相对能量分布特征的分析就是其中的问题之一。

1 地震信号各子带相对能量分布的数学表达

信号的小波多分辨率分解可表达为

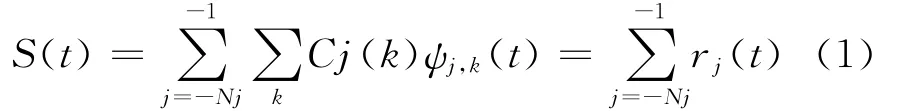
式中S（t）为信号；Cj（k）为小波系数；ψj，k（t）是小波母函数。由于小波簇｛ψj，k（t）｝对L2（R）是 正交的，小波系数由Cj（k）＝＜S，ψj，k＞ 给出，每层的能量就是细节信号的能量：

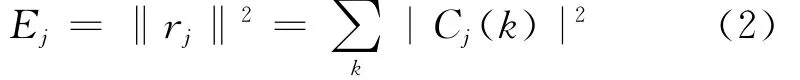
总能量有下式给出：

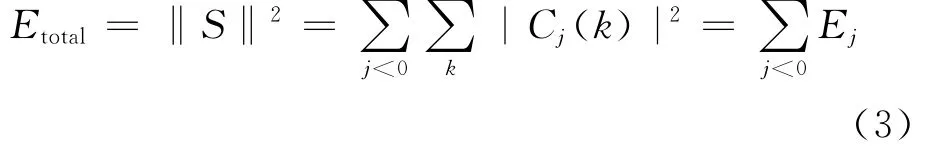
我们定义一个归一化参数ρj表示相对小波能量：

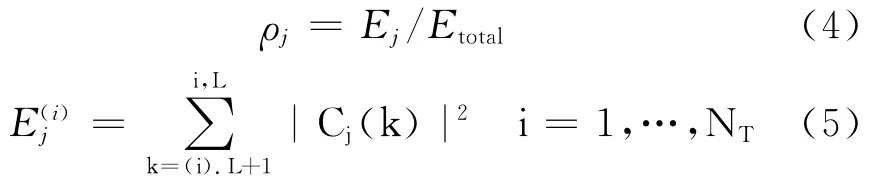
这个时间窗口的总能量为

相对能量分布为

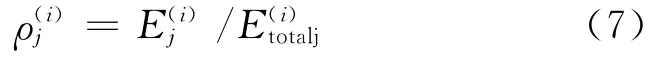
2 各子带相对能量分布的理论测试

2．1 信号构建

构建信号的采样率为100sps．构建的正弦信号分为3段：第一段频率为0．5Hz，第二段频率为5 Hz，第三段频率为15Hz。

2．2 小波基的选择

在信号分析时小波基的选择也很重要。我们在此选择了Daubechies小波。其特点是有较好的紧支撑性、光滑性和近似对称性。小波系数按正整数N分为不同序列（dbN），考虑到地震仪记录地震波的频带范围，在此我们选用db8。

2．3 理论信号的小波分解及结果检验

在Matlab2009a环境下，自编程序实现信号的小波多分辨率分解。图1展示了原始理论信号和信号重构的对比，可见信号没有因分解和重构的处理而发生失真。通过对原始信号和重构信号的偏差统计分析，得到二者的方差（SSE）为1．554 2e－019，均方根差为（RMSE）为7．351 2e－012。可以满足计算分析的要求。

2．4 理论信号的相对能量分布

根据前述信号的相对能量分布的数学表征，对构建信号进行了小波相对能量分布的计算。采用db8小波基将信号分解为8个子带，每个子带对应的频段如表1所示。

结果表明，信号的能量集中在子带2、4、7，对应信号的15Hz、5Hz和0．5Hz，与信号频率一致。从理论信号的处理及测试结果表明，这种方法是有效的、可靠的。

3 实际地震波的计算处理

我们选取了9例2010年甘肃地震台网记录ML3．3～4．2，震源深度5．9～9．2km的地震，进行小波多分辨率的分解及相对小波能量分布计算。所选地震的有关参数来自中国地震台网（表2）。

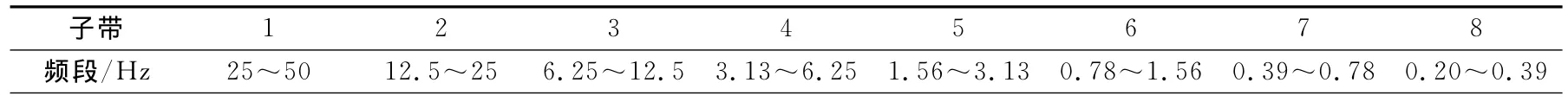
表1 子带与频段对应表Table 1 Corresponding table for frequency band and sub－band

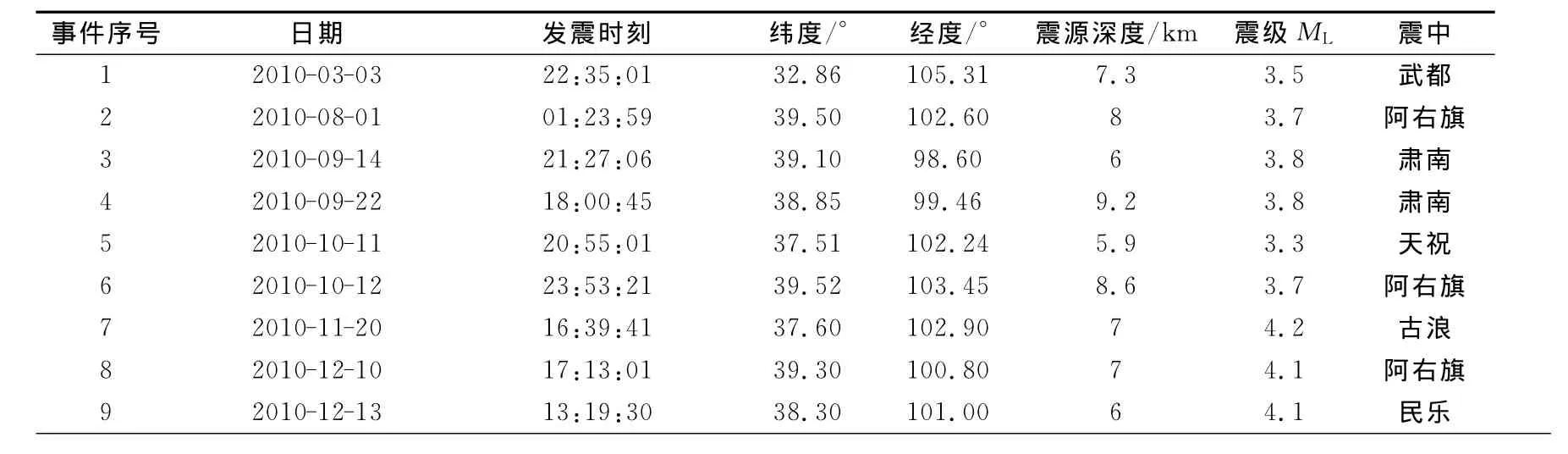
表2 选取的地震参数Table 2 Seismic parameters of selected earthquake

3．1 实际地震信号的小波分解和结果检验

对选取的9例地震记录进行了小波多分辨率分解（db8），并进行信号重建。对重建信号和原始信号的统计检验结果表明，方差（SSE）量级达到10－19，均方根差（RMSE）的量级达到10－12，与理论信号的误差量级一致。图2展示了2010年3月3日武都地震，甘肃文县台垂直向记录的小波多分辨率分解的各层细节和信号重建的波形，可见分解后的细节更清晰的表达了信号的频率特征和在时序上的变化过程，重建信号与原始信号之间偏差极小。

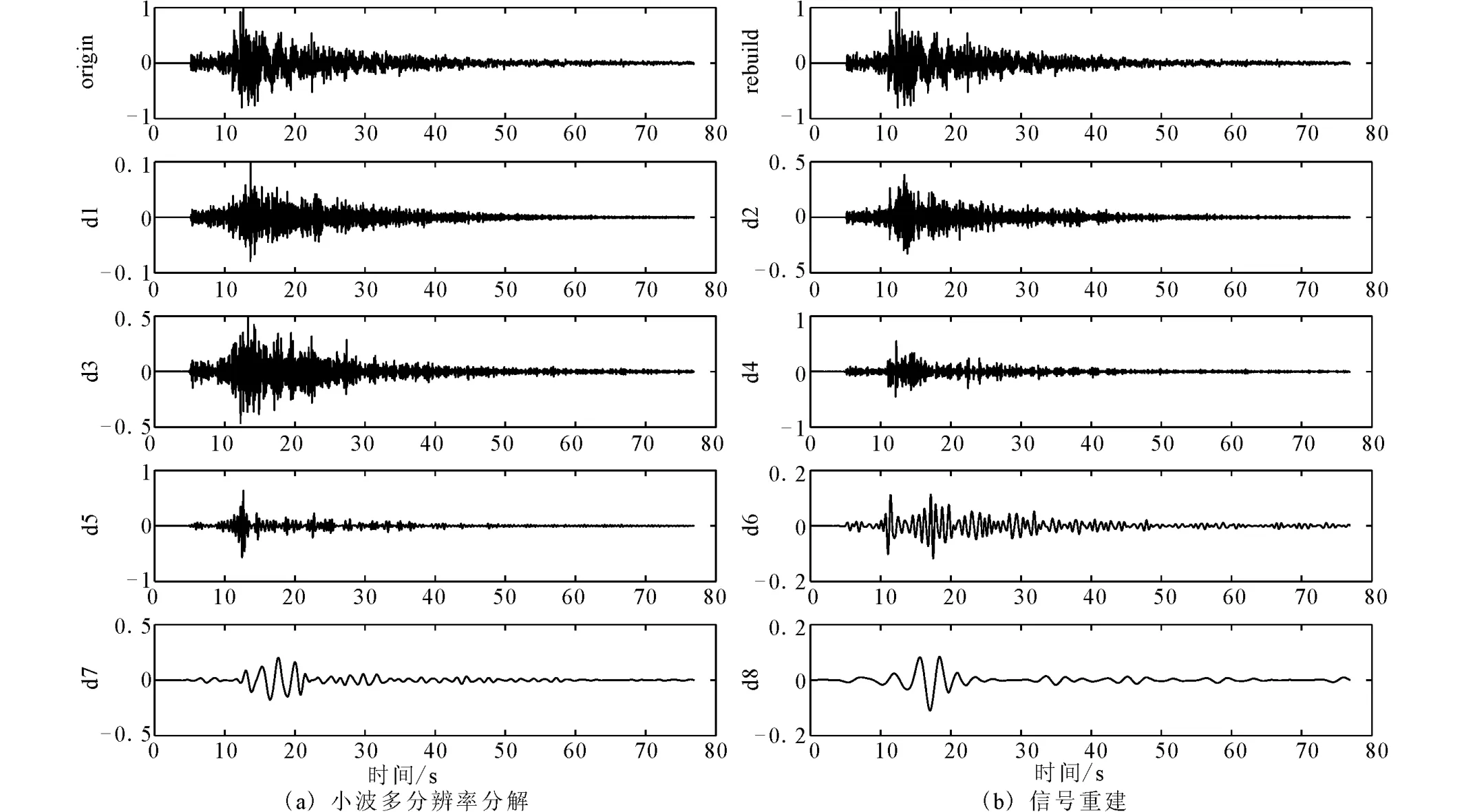
图2 文县台垂直向地震记录的小波多分辨率分解和信号重建（2010－03－03武都地震）Fig．2 Multiresolution decomposition and signal rebuild of Wudu earthquake in 2010recorded by Wenxian seismic station）．

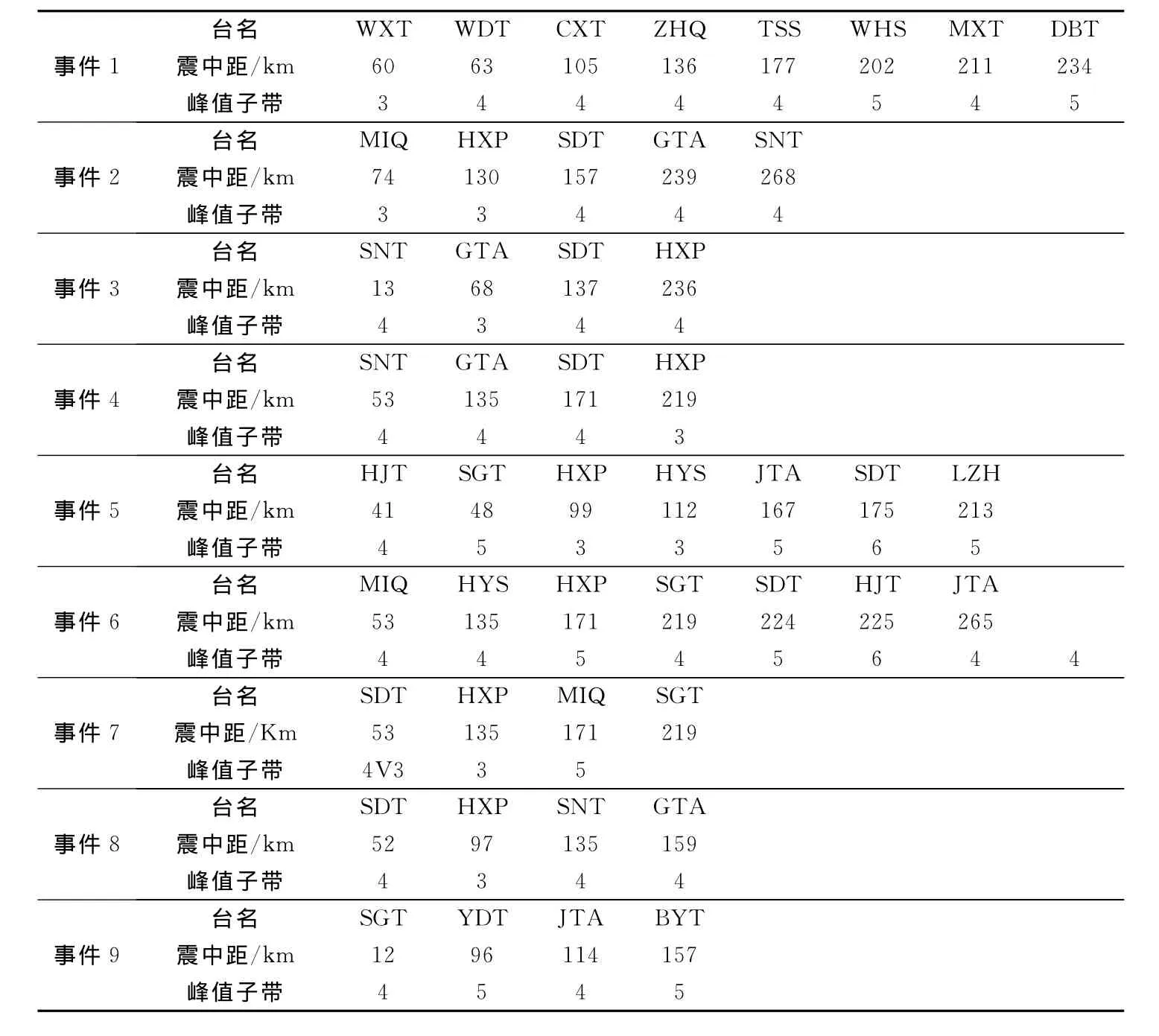
表3 地震波峰值子带Table 3 The sub－band of seismic wave peak

3．2 实际地震波的相对能量分布

采用同样的计算方法，计算了这9例地震一些近台记录垂直向的相对能量分布（表3）。

从表3可见近地震的能量主要集中在3，4，5这3个频率子带，估算的频率范围在1～15Hz，其中，子带4能量峰值最为集中，频率范围为在3～6Hz，同一地震不同台站记录的相对能量分布存在差异。

对不同震中距段内，能量峰值子带的出现概率作了初步统计，结果如表4。可以看出随震中距增大，峰值能量的频率由低向高的走势，这种现象的解释或许是一个需要进一步探求的问题。

表4 地震峰值能量频带的概率统计Table 4 The probability on sub－band of seismic wave peak

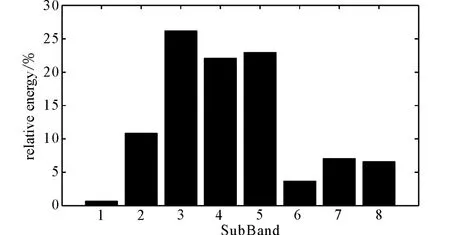
图3 文县台垂直向记录的相对能量分布（2010．03．03武都地震）Fig．3 Distribution of relative energy of Wudu earthquake in 2010recorded by Wenxian seismic sation．

图3给出了2010年3月3日武都地震甘肃文县台垂直向记录的相对能量分布。

4 结果与讨论

（1）基于小波多分辨率分解的后的重建信号与原始信号之间的偏差很小（在10e－12量级上），可以满足信号分析的要求；

（2）将地震信号分解在不同频率的子带上，仍然保留了信号的时间信息，并在一定程度压制了其它杂噪干扰信号，更利于研究地震波在不同频段的时程变化规律，更利于研究震源过程、能量辐射规律和路径介质的各向异性；

（3）近地震的峰值能量频率集中在3～6Hz之间；

（4）地震波相对能量的计算方法可以很好的揭示近地震能量分布在频率域的特征；

（5）由于小波窗长的影响，计算过程会有一些能量泄露，在计算处理时要给予注意和考虑。

［1］ 李英，张淑贞，许康生．小波降噪方法在地震信号处理中的应用［J］．西北地震学报，2006，28（2）：159－162．

LI Ying，ZHANG Shu－zhen，XU Kang－sheng．Application of Wavelet Transfer in Seismic Signal Denoise［J］．Northwestern Seismological Journal，2006，28（2）：159－162．

［2］ 刘希强，沈萍，山长仑，等．数字化地震波形资料的时频分析方法及应用［J］．西北地震学报，2004，26（2）：118－124．

LIU Xi－qiang，SHEN Ping，SHAN Chang－lun，et al．Time－frequency Method and Its Application in Digital Seismic Wave Data Processing［J］．Northwestern Seismological Journal，2004，26（2）：118－124．

［3］ 姚家骏，杨立明，冯建刚．常用时频分析方法在数字地震波特征量分析中的应用［J］．西北地震学报，2011，33（2）：105－109．

YAO Jia－jun，YANG Li－ming，FENG Jian－gang．Application of Common Time－Frequency Analysis Methods in Analyzing Characteristic Quantity of Digital Seismic Wave［J］．Northwestern Seismological Journal，2011，33（2）：105－109．

［4］ 王燕，刘俊民，王晓明，等．地震阈值监测技术中的震级校正［J］，西北地震学报，2011，33（4）：319－321．

WANG Yan，LIU Jun－min，WANG Xiao－ming，et al．Magnitude Calibration of Seismic Threshold Monitoring［J］．Northwestern Seismological Journal，2011，33（4）：319－321．

［5］ 杨福生．小波变换的工程分析与应用［M］．北京：科学出版社，2000：42－68．

YANG Fu－sheng．Application and Engineering analysis of Wavelet Transfer［M］．BeiJing：Science Press，2000：42－68．

［6］ 胡昌华，张军波，夏军，等．基于 MATLAB的系统分析与统计［M］．西安：西安电子科技大学出版社，1999：210－232．

HU Chang－hua，ZHANG Jun－bo，XIA Jun，et al．Statistics and Analysis of System Based on MATLAB［M］．Xi′an：Xi′an University of Electronic Science and Technology Press，1999：210－232．

［7］ 许康生，李秋红，李英．大地震前近台背景噪声的频谱分析［J］．西北地震学报，2012，34（2）：150－153．

XU Kang－sheng，LI Qiu－hong，LI Ying．Analysis on the Spectrum of Background Noise in Stations Near by Epicenters of Two Great Earthquakes［J］．Northwestern Seismological Journal，2012，34（2）：150－153．

［8］ 刘希强，孙亚强，赵冰，等．地震震中实时动态定位的方法研究［J］．西北地震学报，2012，34（4）：342－348．

LIU Xi－qiang，SUN Ya－qiang，ZHAO Bing，et al．Research on Real－time Evolutionary Earthquake Epicentral location［J］．Northwestern Seismological Journal，2012，34（4）：342－348．

［9］ Daubechies I．Orthonormal Bases of Compactly Supported Wavelet［J］．Communication Pure and Applied Mathematics，1988，41（7）：909－996．