水库优化调度中的异轨同效问题
刘 攀,赵静飞,李立平,沈 艳
(武汉大学水资源与水电工程科学国家重点实验室,湖北武汉 430072)
水库优化调度中的异轨同效问题
刘 攀,赵静飞,李立平,沈 艳
(武汉大学水资源与水电工程科学国家重点实验室,湖北武汉 430072)
针对确定性水库优化调度问题,引入近似最短路径方法,寻求优化调度的近似最优解,从而证实“异轨同效”现象存在的可能性。借鉴流域水文模型的“异参同效”研究成果,视隐随机调度问题中的调度规则参数为具有概率分布特征的参数,视调度目标函数为似然函数,采用贝叶斯方法估计最优调度轨迹的区间分布,开展水库调度的最优调度轨迹的等效性研究。实例分析结果表明:进行水库优化调度的“异轨同效”研究,可以估计最优调度轨迹区间,从而将传统调度的单点决策转变为区间决策,更符合调度操作实际情况。
水库优化调度;隐随机调度;异参同效;不确定性分析;近似最优解
水库是人类主动调整水资源时空分布的重要措施,担负着防洪、发电、航运、供水等多方面的功能与任务,成为支撑社会文明进步的重要手段之一。水库调度是实现水库正常运行的必备技术,通过提高水库管理运行水平,达到兴利、除害的目的,可提高水资源和水能资源利用率。由于水资源系统的复杂性,水库优化调度技术仍存在理论上的三大难题:维数灾、多目标性以及不确定性[1-2]。在这三大理论难题中,不确定性的研究相对较少,主要集中在预报入库流量、功能需求(如电网负荷)的不确定性分析等方面,事实上,即使是确定性的水库优化调度问题,也可能存在最优解的“异轨同效”现象,即多个最优调度轨迹存在等效性,这种现象可表现为最优解并不唯一[3]。在传统的水库调度中,通常只保留一个最优解,而忽略其他等效的最优解,这样往往丢失了很多有用的信息。水库优化调度问题中多重解(即多个最优解)的存在,使相同最优解下构建各种可行比较方案成为可能,为决策提供了广泛的选择余地[3-4],具有较大的理论和现实意义。
水文模型中的“异参同效”现象是近年来的热点研究问题[5]。“异参同效”是指对于相同的模型结构和相同的模型输入,会有多个最优参数组使所获得的模型输出具有相同的拟合精度。“异参同效”现象的存在,为在参数识别中有别于传统的寻求唯一最优解的思路,而采用基于不确定分析的方法提供了理论依据。
根据系统理论,水库优化调度是一个最优辨识问题[6],调度轨迹或者调度规则参数均需进行参数识别,传统方法仅采用了优化的思路,如果“异轨同效”(指对于相同的调度模型和相同的模型输入,会有多个最优参数组,如调度轨迹或者调度规则参数,使所获得的调度结果具有相同的目标函数值)现象客观存在,那么采用基于不确定分析的方法来识别参数就具有可能性。
本文针对确定性水库优化调度问题,引入近似最短路径方法,寻求优化调度的近似最优解,从而论证“异轨同效”现象存在的可能性;借鉴流域水文模型的“异参同效”研究成果,视隐随机调度问题中的调度规则参数为具有概率分布特征的参数,视调度目标函数为似然函数,采用贝叶斯方法估计最优调度轨迹的区间分布,开展水库调度的“异轨同效”(多个最优调度轨迹的等效性)研究。
1 确定性水库优化调度的近似最优解
1.1 近似最优解定义
对于单目标确定性水库优化调度问题,传统最优调度方法(如线性规划、非线性规划以及动态规划等)只寻求使目标函数达到最大值E*的调度轨迹,文献[7]将近似最优解定义为使目标函数满足E≥E*(1-ε)的所有解,其中ε(0≤ε≤1)为一个允许误差值。需要指出水库优化调度中全局最优解往往不易获得,这里定义的E*为能得到的最优解(可采用动态规划方法获得);推求近似最优解之前需确定最优解E*。
1.2 近似最短路径方法
确定性水库优化调度是一多阶段决策问题,与最短路径问题相类似,可采用动态规划方法求解。文献[8]提出了近似最优最短路径问题,即寻求长度不超过1+ε倍最短路径长度的所有路径,其中ε(0≤ε≤1)为给定的误差水平。与近似最优最短路径问题相比,前k条最短路径问题(寻找从起点到终点的前k条最短路径)受到了广泛的关注和研究,但这两个问题本质相同,因此可相互转化。前k条最短路径问题可为决策提供更多的选择,应用广泛。求解前k条最短路径问题的方法有Yen方法及其扩展、MPS方法以及Eppstein方法等,这些算法的复杂度都与近似最优解个数呈线性增长关系[9-10]。
2 水库隐随机调度规则的参数不确定性
2.1 隐随机调度与水文模型的类比
自Young[11]提出水库隐随机调度规则提取方法以来,Karamouz等[12]证明拟合最优调度轨迹的最好调度规则不一定效率高,Koutsoyiannis等[13]提出了基于模拟的优化方法。因为以遗传算法为代表的智能算法在求解复杂优化问题方面具有灵活性和通用性,基于模拟的优化算法已成为推求隐随机调度规则的标准方法[14]。
流域水文模型与水库优化调度问题颇具相似之处:目标函数是多极值的;模型中包含的参数(在水库调度中是调度轨迹或者调度规则参数)之间存在相互补偿作用;模型参数具有随机性。本文拟借鉴水文模型中的“异参同效”分析技术,将隐随机调度规则推求问题中的调度规则参数视为具有概率分布特征的参数,将调度目标函数视为似然函数,采用基于贝叶斯理论的不确定性分析技术,研究水库调度中的“异轨同效”现象,即多个最优调度轨迹的等效性问题,从而估计最优调度轨迹区间。
如图1所示,将水库调度规则形式视为模型,调度规则参数视为参数,调度目标函数视为似然函数,采用通用似然不确定性估计法(GLUE)[5]和马尔科夫链蒙特卡罗法(MCMC)[15]等不确定性分析方法代替传统的优化方法,研究参数的后验概率分布,进而根据模拟调度进一步估计最优调度轨迹的区间分布,即认为各种调度规则参数均具有可行性与可能性,只是概率分布不同而已。评价最优调度区间内的可行轨迹的调度效率,从而可验证区间估计的合理性。
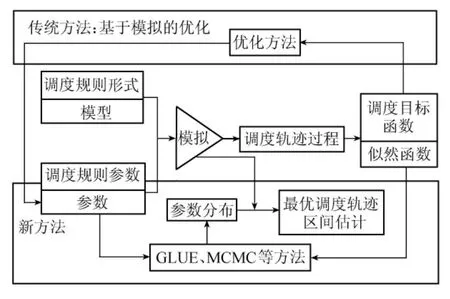
图1 隐随机调度规则推求问题的传统方法与不确定性分析方法
2.2 基于贝叶斯理论的不确定性分析方法
贝叶斯理论在洪水预报和水文模型、水文分析计算以及水环境等领域应用广泛[16-17]。研究“异参同效”不确定性分析的方法很多,国际水文科学协会(IAHS)通过Workshop的方式,在全世界范围内探讨环境科学中的不确定性分析方法,其中常用的有伪贝叶斯方法和贝叶斯统计推断方法。
2.2.1 伪贝叶斯方法
GLUE是目前最常用的不确定性估计的经验频率方法,它的原理与轨迹区间估计步骤如下:
a.假设水库调度目标函数中参数的先验分布是均匀分布,通过随机模拟取样方法生成一定数目的可行参数组。

c.这些具有权重的参数组就是参数的后验分布,取其经验分布即可估计区间的分布。
2.2.2 贝叶斯统计推断方法
常用的改进方法为AM-MCMC算法[18],可不需给定参数的先验分布,轨迹区间估计步骤如下:
a.设水库调度规则有n个参数,随机生成i组(如 i=100)矢量参数组 θk(k=1,2,…,i),计算相应的调度目标函数值。
b.利用式(1)计算矢量参数组样本的协方差矩阵
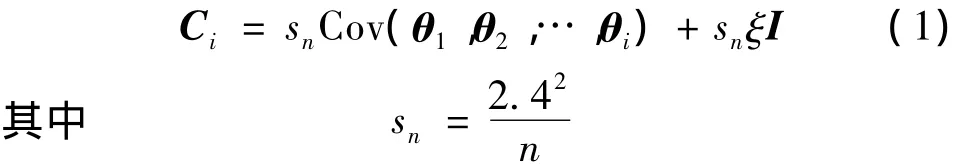
式中:I为n维单位矩阵;ξ为0.01~0.1之间的随机数。
c.生成新的矢量参数组样本θi+1服从多维正态分布 N(θi,Ci)。
d.将新的矢量参数组样本θi+1代入模拟模型进行计算,得到目标函数值Fi+1。
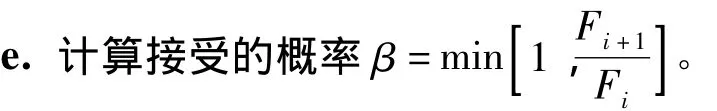
f.产生0~1之间的随机数α,如果α< β,则θi+1=θi+1,否则 θi+1=θi。
g.i=i+1,重复步骤b至f,直到生成足够的矢量参数组数(如5000)为止。
h.这些矢量参数组就是参数的后验分布,取其经验分布估计调度轨迹区间的分布。
3 实例分析
三峡水库具有防洪、发电、航运等多项综合效益,是世界上最大的水利水电工程,水电站单机容量、总装机容量、年发电量均居世界第一。三峡水库属于季调节或不完全年调节,调度涉及枯季补水、汛期防洪等多方面的需求。开展三峡水库优化调度,社会经济效益显著。选用三峡1882—2003年旬径流系列资料进行分析。
3.1 优化调度模型
本文仅采用发电单目标,目标函数为

式中:m为水库调度时段数;Δt为时段长度;Ni为时段 i的出力,Ni=min[KRihi,f(hi)],其中 K 为综合出力系数,hi为时段i的发电水头,Ri为时段i的出库流量,f(hi)为机组的出力限制线。
约束条件为

式中:Ii为第i时段的入库流量;Vi为时段i的水库库容;ei为时段i的蒸发渗漏等损失(本文忽略不计)。
3.2 近似最优解
在入库流量已知的条件下,根据上述目标和约束条件建立确定性水库优化调度模型。采用近似最短路径方法,给定误差水平,得到各代表年的多个近似最优解。列出1895年的8个近似最优解如图2所示,其最优解为893.4亿kW·h,相应的目标函数值也列在图中,可以看出调度轨迹虽然不同,但调度运行的目标函数值基本相同,说明近似最优解客观存在。

图2 具有相近的目标函数值的8个调度轨迹
表1给出了当误差为0.01%时,取不同离散个数离散水库库容,得到的近似最优解个数和相应的计算时间。可以看出:①随着离散个数的增加,近似最优解个数增加较快,近似为指数增长关系;②计算时间也近似指数增长;③如果将寻求最优解和近似最优解的时间相比,当离散个数不大时,取决于寻求最优解的时间;反之则取决于寻求近似最优解的时间。
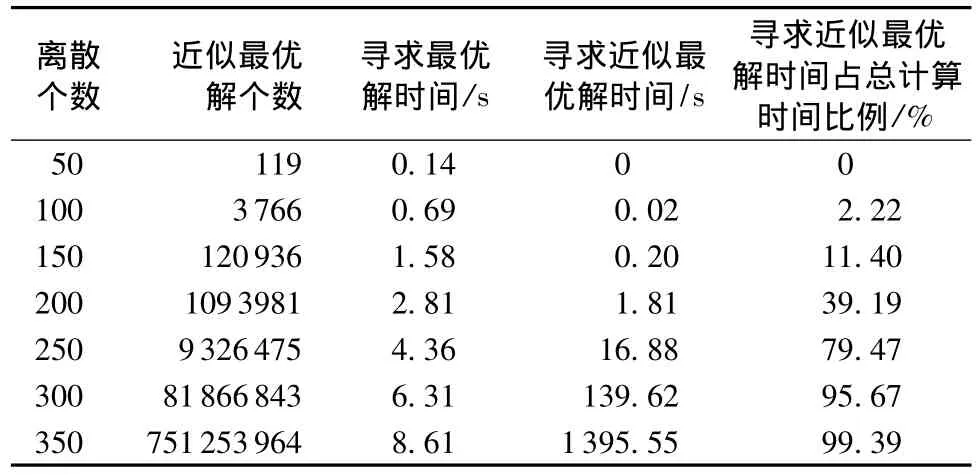
表1 误差为0.01%时近似最优解个数、计算时间与离散个数之间的关系
同样,随着误差水平的增加,近似最优解个数和计算时间也为指数增长关系;随着时段个数的增加,近似最优解个数和计算时间也为指数增长关系。
因此,近似最优解的算法复杂度依赖于离散个数、误差水平以及计算时段个数等。文献[9]指出前k条最短路径问题的复杂度为O(k+p+qlgq)(其中k为近似最短路径条数,p和q分别为路径的节点和边的条数),这是目前复杂度最低的算法。由于近似最优解的个数与离散个数、误差水平以及计算时段个数均呈指数增长关系,因此计算时间也呈指数增长。
取所有近似最优解的上、下包线作为边界,可形成一个近似最优调度域,其意义在于:水库在近似最优调度域内调度运行不一定能获得近似最优调度策略;一旦超出了这个边界,则一定无法获得满足E≥E*(1-ε)的目标值(近似最优解)。
1895年的近似最优调度域如图3所示[7],可以看出:①误差越大,得到的近似最优调度域范围越宽;②水库汛前清空库容和汛末蓄水的调度域宽度很窄,说明此时调度非常关键,属于关键调度时期,这一点与调度经验相符;③最优调度域可提供多个决策,为多目标决策提供直观决策。如汛期为满足防洪要求,运行水位越低越好。根据最优调度域,可将汛期的运行水位适当降低,这样损失电量不多,但可大幅度提高防洪效益。
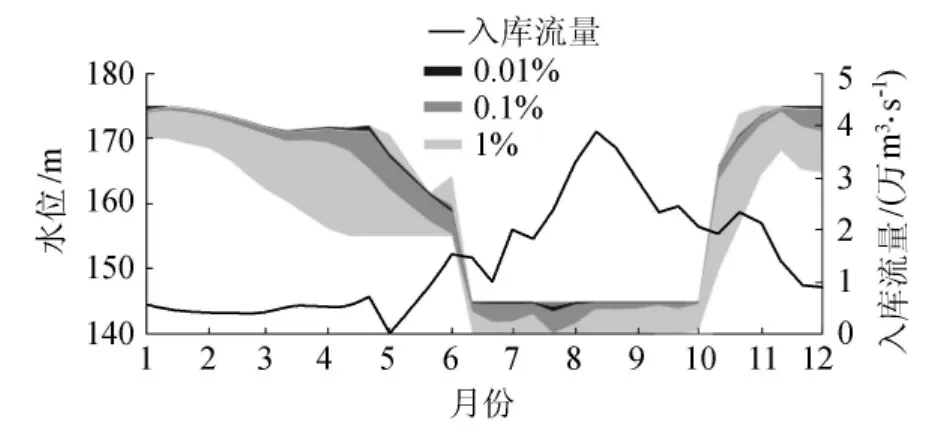
图3 不同误差水平下的近似最优调度域
3.3 调度规则不确定性分析
采用隐随机优化方法开展三峡水库中长期调度,采用简单的线性调度规则,即
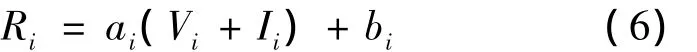
式中:ai和bi为水库调度规则参数,需通过模拟优化方法确定,在这里分析其不确定性。基于模拟仿真,采用不确定性分析技术,最终得到了参数估计与最优调度决策估计,如图4所示。可以看出,相对于单一调度决策,不确定分析指出调度不一定需严格地控制水库水位在170 m左右。
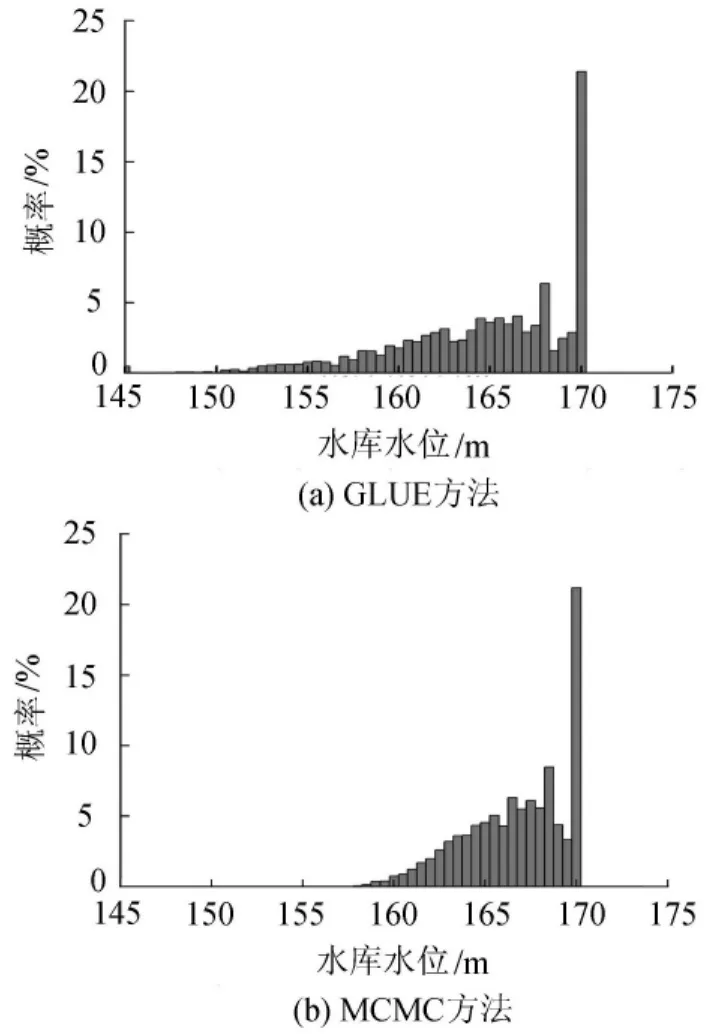
4 2002年10月中旬最优水库水位概率分布
4 结语
开展水库调度的“异轨同效”研究,不仅可以从理论上分析探讨多个最优调度轨迹邻近区域的调度效率等问题,还能估计最优调度轨迹区间,提高水库优化调度技术的实用性水平,充分发挥水库优化调度投资少、效益大、需求高、前景广等优点,显著提高水库的综合效益。但开展水库调度的“异轨同效”研究还处于起步阶段,如何提高优化算法效率并将最优调度轨迹区间应用于实际调度等问题,尚需深入研究。
[1]YEH W W-G.Reservoir management and operations models:a state-of-the-art review[J].Water Resources Research,1985,21(12):1797-1818.
[2]LABADIE J.Optimal operation of multireservoir systems:state-of-the-art review[J].Journal of Water Resources Planning and Management,2004,130(2):93-111.
[3]叶秉如,董增川,许静仪,等.线性规划问题的多重解及其寻求[J].河海大学学报:自然科学版,2005,33(2):224-231.(YE Binru,DONG Zengchuan,XU Jingyi,et al.Multivalued solution of linear program and the way to find it[J].Journal of Hohai University:Natural Sciences,2005,33(2):224-231.(in Chinese))
[4]刘攀,郭生练,张越华,等.水电站机组间最优负荷分配问题的多重解研究[J].水利学报,2010,41(5):601-607.(LIU Pan,GUO Shenglian,ZHANG Yuehua,et al.Multiple solutions of optimal load allocation of generators in hydropower stations[J].JournalofHydraulic Engineering,2010,41(5):601-607.(in Chinese))
[5]BEVEN K,FREER J.Equifinality,data assimilation,and uncertainty estimation in mechanistic modeling of complex environmental systems using the GLUE methodology[J].Journal of Hydrology,2001,249:11-29.
[6]张勇传.系统辨识及其在水电能源中的应用[M].武汉:湖北科技出版社,2008.
[7]LIU P,CAI X,GUO S.Deriving multiple near-optimal solutions to deterministic reservoir operation problems[J].Water Resources Research,2011,47(8),W08506.doi:10.1029/2011WR010998.
[8]BYERS T H,WATERMAN M S.Determining all optimal and near-optimal solutions when solving shortest path problemsby dynamic programming[J].Operation Research,1984,32(6):1381-1384.
[9]EPPSTEIN D.Finding the k shortest paths[J].SIAM Journal on Computing,1998,28(2):652-673.
[10]HERSHBERGER J,SURI S,BHOSLE A.On the difficulty of some shortest path problems[J].ACM Transitions on Algorithms,2007,3(1):1-15.
[11]YOUNG G K.Finding reservoir operating rules[J].Journal of Hydraulics Division,1967,93(6):297-321.
[12]KARAMOUZ M,HOUCK M.Annual and monthly reservoir operating rules generated by deterministic optimization[J].Water Resources Research,1982,18(5):1337-1344.
[13]KOUTSOYIANNIS D,ECONOMOU A.Evaluation of the parameterization-simulation-optimization approach for the controlofreservoirsystems[J].WaterResources Research,2003,39(6):1170-1186.
[14]刘攀,郭生练,李玮,等.遗传算法在水库调度中的应用综述[J].水利水电科技进展,2006,26(4):78-83.(LIU Pan,GUO Shenglian,LI Wei,et al.A review of application of genetic algorithm to reservoir operation[J].Advances in Science and Technology of Water Resources,2006,26(4):78-83.(in Chinese))
[15]VRUGT J A,GUPTA H V,BOUTEN W,et al.A shuffled complex evolution metropolis algorithm for optimization and uncertain assessment of hydrologic model parameters[J].Water Resources Research,2003,39(8):1201-1218.
[16]REIS D S,STEDINGER J R.Bayesian MCMC flood frequency analysis with historical information[J].Journal of Hydrology,2005,313:97-116.
[17]邢贞相,芮孝芳,崔海燕,等.基于AM-MCMC算法的贝叶斯概率洪水预报模型[J].水利学报,2007,38(12):1500-1506.(XING Zhenxiang,RUIXiaofang,CUI Haiyan,et al.Bayesian probabilistic flood forecasting model based on adaptive Metropolis MCMC algorithm[J].Journal of Hydraulic Engineering,2007,38(12):1500-1506.(in Chinese))
Equivalence of reservoir optimal operation
LIU Pan,ZHAO Jingfei,LI Liping,SHEN Yan(State Key Laboratory of Water Resources and Hydropower Engineering Science,Wuhan University,Wuhan 430072,China)
In order to solve the problem of the reservoir optimal operation,the near-optimal solution of the reservoir operation was obtained using the shortest path method.Based on the research of hydrological models,the interval distributions and the equivalences of different operation tracks were analyzed using the Bayesian method when the operation rule parameters of the implicit stochastic operation were probability distributions and the reservoir operation objective function was regarded as the likelihood function.The results show that the research on the equivalences of different operation tracks of the reservoir operation can be used to obtain the interval distributions of the optimal operation tracks.Based on the interval distributions,the single point decision making method can be transformed into the interval decision making method,which is consistent with the practice.
deterministic reservoir operation;implicit stochastic operation;the equivalences of different operation tracks;uncertainty analysis;near-optimal solution
TV697.1+1
A
1006-7647(2013)02-0005-04
10.3880/j.issn.1006-7647.2013.02.002
“十一五”国家科技支撑计划(2009BAC56B04,2009BAC56B02);国家自然科学基金(50979072);教育部新世纪优秀人才支持计划(NCET-11-0401)
刘攀(1978—),男,湖南湘潭人,副教授,博士,主要从事水文及水资源开发利用研究。E-mail:liupan@whu.edu.cn
2012-06-05 编辑:周红梅)

