鄂尔多斯盆地D区常规测井裂缝孔隙评价

陈世海，李 璟，任俊松，李鸿范

（陕西延安石油天然气有限公司，陕西西安 710018）

深、浅双侧向测井电阻率曲线间的差异与裂缝孔隙流体性质、产状及其发育程度、泥浆及基岩电导率特性等因素有关[1]。利用双侧向电阻率间的差异可定性识别裂缝，并可对裂缝孔隙度参数进行定量评价。常用的裂缝孔隙模型包括：Sibbit建立的含水裂缝孔隙模型和含油气裂缝孔隙模型[2]；Pezard和Anderson建立的计算近水平裂缝孔隙度和近垂直裂缝孔隙度模型（1990，简称P-A模型）[3]；网状裂缝孔隙度模型[4]；李善军利用三维有限元法建立的裂缝孔隙模型（1996）[5]。本文从原理上对各种模型适用条件进行了对比分析，对目标区裂缝孔隙进行了评价。

1 Sibbit裂缝孔隙模型

该模型重点考虑了裂缝孔隙流体对电阻率的影响，没有考虑裂缝产状及其开度对电阻率的影响[2]。

含油裂缝孔隙模型：

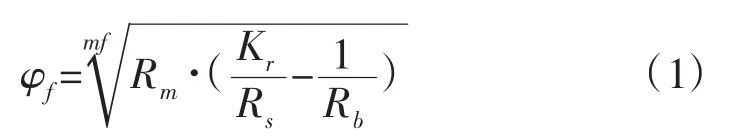
含水裂缝孔隙模型：

其中：mf为裂缝孔隙度指数，一般取1.059～1.119；Kr为双侧向畸变系数（低角度缝1.2，倾斜裂缝1.1,高角度缝 1.0）；Rb、Rs、Rw、Rm分别为基岩、浅侧向、地层水及泥浆滤液电阻率，单位Ω·m。

2 Pezard-Anderson裂缝孔隙模型

将平行等间距的裂缝性地层等效为宏观均匀各向异性介质，推导任意倾角条件下裂缝性地层的双侧向测井响应，给出用于计算近水平及近垂直裂缝孔隙度的评价模型。判断裂缝产状的依据是双侧向测井响应正负差异，正差异（Rd＞Rs）为近垂直裂缝，负差异（Rd＜Rs）为近水平裂缝[3-7]。

近水平裂缝孔隙模型：

近垂直裂缝孔隙模型：

其中：Cf是裂缝孔隙流体电导率，S/m；孔隙充满地层水时为Cw，充满泥浆滤液时为Cm；Cd、Cs为深、浅侧向电导率，S/m。

3 网状裂缝孔隙模型

网状裂缝性地层简化模型（见图1），设裂隙网格长度相对大小为x，假设裂缝孔隙内饱含水，根据并联导电模型，利用双侧向测井资料推导网状裂缝孔隙模型[4]：

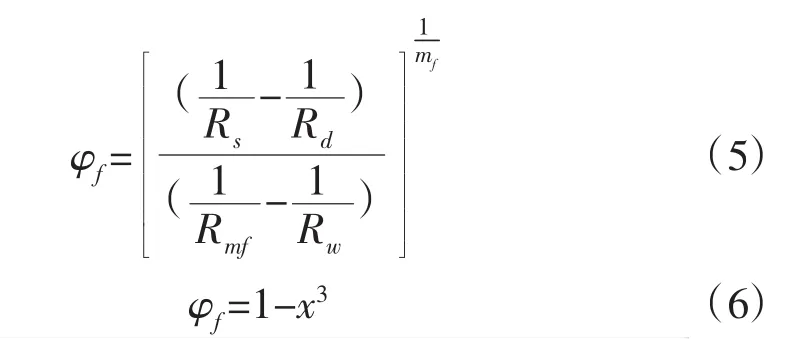
地层因子F：

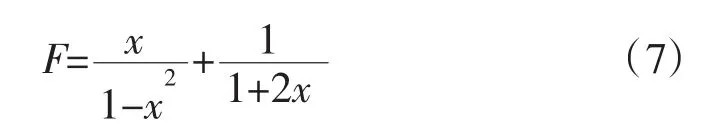
利用迭代算法可求得裂缝孔隙度φf，步骤如下：

①假设 mf=1，根据（5）式计算 φf1；②将 φf1带入（6）式，求取 x，然后利用式（7）、（8）求 mf；③再次利用（5）式计算φf2，比较两次计算误差；④若误差满足精度要求则停止迭代，否则令φf1=φf2，重新由（6）式计算，直到精度满足要求为止。

4 三维有限元裂缝孔隙模型

1996年，李善军根据裂缝性地层非均质性特点，利用三维有限元法建立了裂缝性地层电导率正演模型，根据裂缝性地层的双侧向测井响应的特征，给出了判断裂缝倾角的方法，将裂缝分为低角度缝、倾斜缝和高角度缝3种状态，并分别推导了3种状态下裂缝性地层的双侧向测井响应与地球物理参数间的函数关系。裂缝性地层的双侧向测井响应（电导率）数学模型可用下式表示（令 x=φfσf）[8-10]：

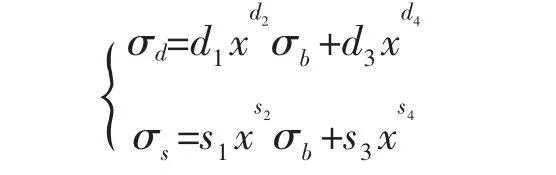
求出满足上式的最佳x值，即可求得裂缝孔隙度φf。因上式为近似相等，根据误差最小原则，利用二分法可确定最佳x0，从而计算裂缝孔隙度：

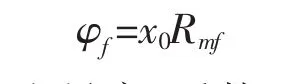
其中 σb为基岩电导率；系数 d1～d4、s1～s4根据裂缝产状分析得到（见表1）。

5 应用实例

利用成像测井资料对目标区D1井裂缝产状进行判断，如图2第4道所示。基于双侧向测井资料，分别利用网状模型及三维有限元模型对D1井不同类型裂缝的孔隙度进行评价，其中网状裂缝发育段采用网状模型，单条裂缝发育段采用三维有限元模型。如图2所示，双侧向计算结果与成像测井解释结论对比相关系较高，效果较好；如图3所示，双侧向计算裂缝孔隙度与成像测井解释裂缝孔隙度交会散点基本均匀分布于45°线两侧，相关程度较高，误差较小。

6 认识与结论

通过对各种常用双侧向裂缝孔隙模型建模方法及其适用条件进行分析，取得如下认识：

（1）Sibbit模型重点考虑了裂缝孔隙流体对电阻率的影响，没有考虑裂缝产状及开度对电阻率的影响，模型参数包括泥浆电阻率、基岩电阻率、地层水电阻率、孔隙含流体性、裂缝孔隙度指数及双侧向畸变系数等，参数较多，难以准确确定。根据实际资料处理对比，模型效果一般，误差相对较大。

表1 裂缝产状系数表（据李善军，1997）

（2）P-A模型优点是参数少，只需确定裂缝孔隙流体电导率Cf。适用于计算单条近水平及近垂直裂缝孔隙度，而实际地层条件下，近水平及仅垂直裂缝发育比例较少，以发育中、高角度裂缝为主，模型适用性受到限制。

（3）网状模型建模采用并联导电模型，利用迭代算法计算裂缝孔隙度，适用于网状裂缝发育段的裂缝孔隙评价。通过实际资料处理，该模型计算误差较小，适用性较强。

（4）三维有限元模型所需参数包括泥浆电阻率和基岩电阻率，可计算任意倾角的单条裂缝孔隙度，并给出判断裂缝产状的方法。通过实际资料处理，该模型误差较小，适用性较强。

［1］汪涵明，张庚骥，李善军，等.单一倾斜裂缝的双侧向测井响应［J］.石油大学学报（自然科学版），1995，19（6）:21-24.

［2］Sibbit AM，Faivre Q.The dual laterolog response in fractured rocks［C］.SPWLA 26th Annual Logging Symposium，Dallas，Texas，1985:17-20.

［3］Philippe A P，Roger N A.In situ measurement of electrial resistivity，formation anisotropy and tectonic context［C］.SPWLA 31th Annual Logging Symposium，Lafayette，Louisiana，1990:24-27.

［4］陈义国，赵谦平，杨文博，等.双侧向测井裂缝孔隙模型考察及改进［J］.大庆石油地质与开发，2011，30（4）:171-174.

［5］李善军，汪涵明，肖成文，等.碳酸盐岩地层中裂缝孔隙度的定量解释［J］.测井技术，1997，21（3）:205-214.

［6］张福明，陈义国，邵才瑞，等.基于双侧向测井的裂缝开度估算模型比较及改进［J］.测井技术，2010，34（4）:339-342.

［7］李军，张超谟，肖成文，等.库车地区砂岩裂缝测井定量评价方法及应用［J］.天然气工业，2008，28（10）:25-27.

［8］匡立春.裂缝孔隙度指数mf的选择探讨［J］.地球物理测井，1990，14（4）:234-236.

［9］刘兴刚，张旭.测井裂缝参数估算方法研究［J］.天然气工业，2003，23（4）:31-34.

［10］王晓畅，范宜仁.基于双侧向测井资料的裂缝孔隙度计算及其标定［J］.物探化探计算技术，2008，30（5）:377-380.