基于乘车舒适性的高速铁路轨道高低不平顺谱限值估计方法
田国英,高建敏,刘鹏飞
(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
基于乘车舒适性的高速铁路轨道高低不平顺谱限值估计方法
田国英,高建敏,刘鹏飞
(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
应用车辆—轨道耦合动力学理论和平稳随机过程理论,借助车辆—轨道垂向耦合频域分析模型,以轨道高低不平顺谱为输入激励,提出基于车辆垂向舒适性指标(车体加速度和Sperling指标)估计高低不平顺谱限值的方法。以我国武广客运专线及德国低干扰轨道高低不平顺谱为例,对350 km/h行车速度时的谱限值进行了估计。通过对比时域、频域模型计算结果,对所估计谱限值进行了校核,校核分析结果表明,频域模型计算结果与时域结果吻合较好,说明了所估计谱限值的合理性。分析方法及研究结果可为高速铁路轨道不平顺管理提供参考。
高速铁路 高低不平顺 车辆—轨道耦合动力学 功率谱密度
轨道不平顺是引起车辆、轨道等结构物振动和破坏的主要原因。目前,对轨道不平顺主要采用幅值管理和轨道质量指数(TQI)管理,但两种方法都存在一定局限性[1]。轨道不平顺谱不仅能反映 TQI信息,还能提供轨道不平顺幅值和波长特性。因此,结合现有幅值管理和轨道质量指数管理,利用轨道不平顺谱评价轨道状态,评估行车安全性和舒适性,指导轨道养护维修是较为有效和合理的手段[2]。因此,应将轨道不平顺谱作为轨道质量的控制指标之一,纳入到轨道不平顺管理体系。目前,针对轨道谱限值方面的研究尚十分缺乏,以往的研究主要围绕轨道不平顺的幅值限值展开[3-7],因而有必要开展轨道谱限值的研究,以便早日将轨道谱纳入轨道管理体系中。基于以上目的,本文应用车辆—轨道耦合动力学理论和平稳随机过程理论,借助车辆—轨道垂向耦合频域分析模型,以轨道高低不平顺谱为输入激励,提出基于车辆垂向舒适性指标(车体加速度和Sperling指标)的高速铁路轨道高低不平顺谱限值估计方法,并以武广客运专线和德国低干扰高低不平顺谱为例,估计其限值并对所估计限值进行校核,说明了方法的合理性。
1 高低不平顺谱限值估计方法
在估计高低不平顺谱限值时,作以下假设:
1)轨道高低不平顺是服从正态分布的平稳随机过程。
2)轨道谱限值与原谱线是倍数关系,即轨道谱限值的曲线形状与原谱线相同。
3)用于分析计算的动力学模型为线性或弱线性系统,因此响应也是服从正态分布的平稳随机过程。
根据上述假设,首先基于已有高低不平顺谱,利用车辆—轨道垂向耦合频域分析模型计算车体心盘处垂向加速度响应功率谱;根据3σ规则估计车体垂向加速度可能最大值,同时推导车体垂向加速度功率谱与Sperling指标间关系,得到其 Sperling指标值;根据车体垂向加速度和Sperling指标限值,反推高低不平顺谱的增大倍数,从而得到基于舒适性指标的高低不平顺谱限值;最后利用时域数值模拟方法,比较时域、频域结果以校核所估计谱限值的正确性。
1.1 车体心盘处垂向加速度功率谱
车辆—轨道垂向耦合动力学模型[8]如图1所示,利用文献[9]的等效线性化方法,将轮轨间非线性赫兹接触进行线性化处理,得到了车辆—轨道垂向耦合动力学频域分析模型,运用该模型可直接计算车体心盘处垂向振动加速度响应功率谱。
对于该频域分析模型,最终可形成二阶常系数线性微分方程组

图1 车辆—轨道垂向耦合动力学模型

式中:[M]为系统惯量矩阵;[C]为系统阻尼矩阵;[K]为系统刚度矩阵;[Kf]为系统转换矩阵;{Z0}为轨道不平顺输入向量;、{}和{q}分别为系统广义加速度、速度和位移向量。
令{Z0}={I}eiωt,则{q}={H(ω)}eiωt,带入式(1),得到
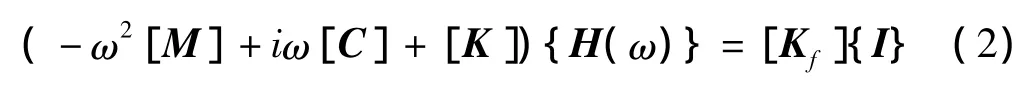
令[D]= -ω2[M]+iω[C]+[K]可得方程

式中,{H(ω)}为某一频率下轨道不平顺与各自由度位移的传递函数向量。不平顺输入间隔向量{I}为

式中:τ1=2lt/V,τ2=2lc/V,τ3=2(lc+lt)/V分别为第二位、第三位和第四位轮对与第一位轮对输入不平顺的时间差;V为车速;lc和lt分别为车辆定距和转向架轴距之半。引入不平顺输入向量后,便可将四位轮对输入{Z0}转换为单一输入 Z0=eiωt。通过求解式(3)的非齐次复系数线性代数方程组的解,从而最终得到系统传递函数矩阵[H(ω)]。
根据系统传递函数矩阵[H(ω)],高低不平顺与车体心盘处垂向振动加速度的传递函数HVCA(ω)为

式中,H1(ω),H2(ω)分别为车体沉浮和点头位移传递函数。利用频域输入输出关系,当输入的高低不平顺谱为 SVI(ω)时,车体心盘处垂向振动加速度谱SVCA(ω)可表达为
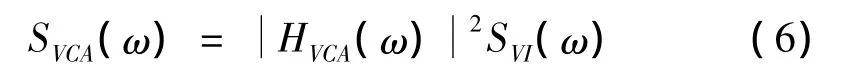
1.2 高低不平顺谱限值估计
根据平稳随机过程的性质可估计车体垂向加速度响应的均方值σ和最大值qmax_VCA分别为
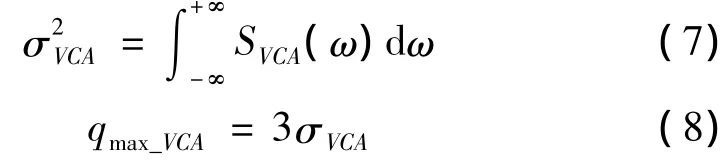
根据式(7)和式(8)及车体垂向加速度幅值限值,运用比例关系,可推导车体垂向加速度幅值限值对应的高低不平顺谱限值相对原谱线幅值的增大倍数kVCA
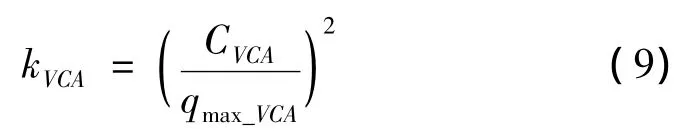
式中,CVCA为给定的车体心盘处垂向加速度指标限值。
根据文献[10]的数值模拟方法,功率谱幅值与频谱幅值的关系为
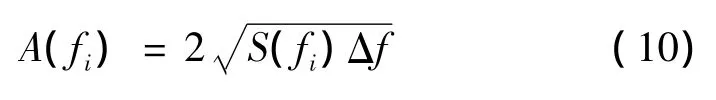
式中,A(fi)为频率fi处的频谱幅值,S(fi)为频率fi处的功率谱幅值,Δf为频域采样间隔,可依据GB 5599—85[11]中规定的采样时间长度确定,文中取 0.05 Hz。将式(10)带入Sperling指标计算公式得
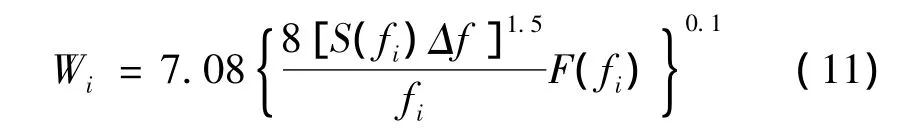
总的Sperling指标为

其中常数 D=8 ×7.0810Δf1.5。
设使Sperling指标达到其给定限值Wlimit时的高低不平顺谱为原谱线的kW倍,则

式(12)与式(13)比较得

由车体垂向加速度和Sperling指标限值确定的轨道高低不平顺谱限值Slimit_VCA(ω)和Slimit_W(ω)分别为

当以Slimit_VCA(ω)或Slimit_W(ω)作为输入时,车体心盘处垂向加速度响应的最大值或Sperling指标将与给定的舒适度指标限值相同。
1.3 高低不平顺谱限值校核
对于由频域分析模型估计的高低不平顺谱限值,有必要将其转换至时域进行校核以分析其正确性。目前,最常用的校核频域计算结果的方法为Monte-Carlo法,其基本思想是概率论中基于大数定理的逼近原理,系统响应的统计特性可从大量响应样本中近似获得,且近似程度随响应样本数的增加而提高[12]。
为此,通过数值模拟方法[10]将轨道高低不平顺谱限值转换成多个高低不平顺样本,利用时域车辆—轨道垂向耦合动力学程序(考虑轮轨接触非线性),计算车体心盘处垂向振动加速度响应。通过以下3方面的对比分析,来验证所估计的高低不平顺谱限值的合理性和正确性。
1)比较时域、频域响应的均方根值。
2)核对时域响应幅值超过车体垂向加速度指标限值概率是否满足3σ规则[13]。
3)计算时域车体心盘处垂向振动加速度响应垂向Sperling指标,分析其是否与频域模型计算的Sperling指标值接近。
2 数值算例
选取我国高速车辆,以武广客运专线轨道高低不平顺平均谱及德国低干扰高低不平顺谱为输入激励,计算了350 km/h行车速度下的车体垂向加速度功率谱响应。依据《高速铁路设计规范(试行)》[14](TB 10621—2009),车体垂向加速度幅值限值(CVCA)为0.13g,Sperling指标限值(Wlimit)取2.5,估计不同速度下的高低不平顺谱限值。最后对所估计的谱限值进行校核。
武广客运专线高低不平顺平均谱及德国低干扰高低不平顺谱表达式为
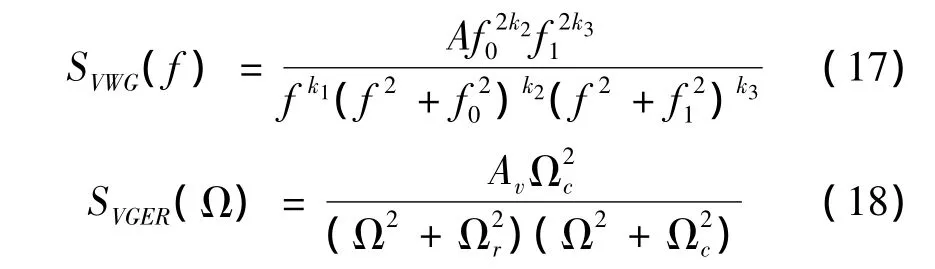
相关参数定义详见文献[8,15],分析波长范围取2~200 m[15]。经单位变换,其功率谱密度曲线如图 2所示。

图2 典型高速铁路轨道高低不平顺功率谱密度
2.1 车体垂向加速度功率谱响应特征
基于式(6)的输入输出关系,分别以式(17)、式(18)作为输入,计算了车体心盘处垂向振动加速度功率谱响应,如图3所示。
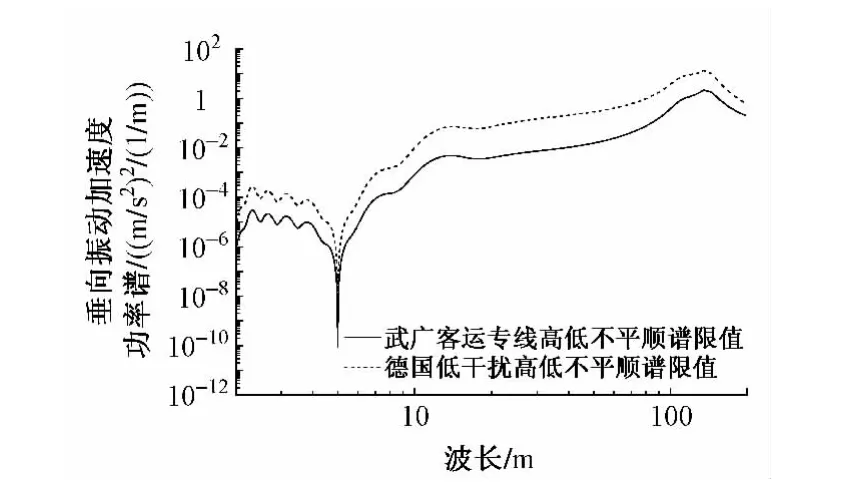
图3 车体心盘处垂向振动加速度功率谱
由图3可见,对于武广谱和德国谱,车体心盘处垂向振动加速度功率谱曲线形状十分相似,幅值随波长增长呈增大趋势,车体心盘处垂向加速度主频集中在135 m左右。
2.2 高低不平顺谱限值
根据式(8)和式(12),计算车体心盘处垂向振动加速度响应的可能最大值及其垂向Sperling指标值,如表1所示。由表1可知,德国谱激扰下的车体垂向加速度响应最大值及垂向Sperling指标均大于武广谱激扰下的指标值,但两种高低不平顺谱激扰下的指标值均较小,未超过各自限值。其中,武广谱激扰下的响应很小,反映了武广客运专线轨道的高平顺性。

表1 乘车舒适性指标值
据式(15)和式(16),武广客运专线和德国低干扰轨道高低不平顺谱,由车体垂向加速度和Sperling指标限值确定的轨道高低不平顺谱限值SLimit_VCA(ω)和Slimit_W(ω)如图4所示。
由图4可见,尽管武广谱和德国谱曲线线形不尽相同,但它们对应的限值谱总体较为接近。在2~5 m波长范围内,德国谱限值与武广谱限值幅值相当;在5~120 m波长范围内,武广谱限值略低于德国谱限值;在120~200 m波长范围内,武广谱限值则高于德国谱限值。

图4 武广客运专线和德国低干扰轨道高低不平顺谱限值

表2 高低不平顺谱限值对应的时域不平顺最大值
根据3σ规则,由式(8)可估算上述谱限值对应高低不平顺幅值的可能最大值,如表2所示。由表2可知,武广谱和德国谱限值对应的高低不平顺最大值十分接近;对于武广谱和德国谱,车体垂向加速度指标对应谱限值的高低不平顺幅值均小于Sperling指标对应谱限值的高低不平顺幅值,即相比Sperling指标,车体垂向加速度更容易出现超标。
利用数值模拟方法[10],将各谱限值转换成时域不平顺样本,如图5和图6所示。
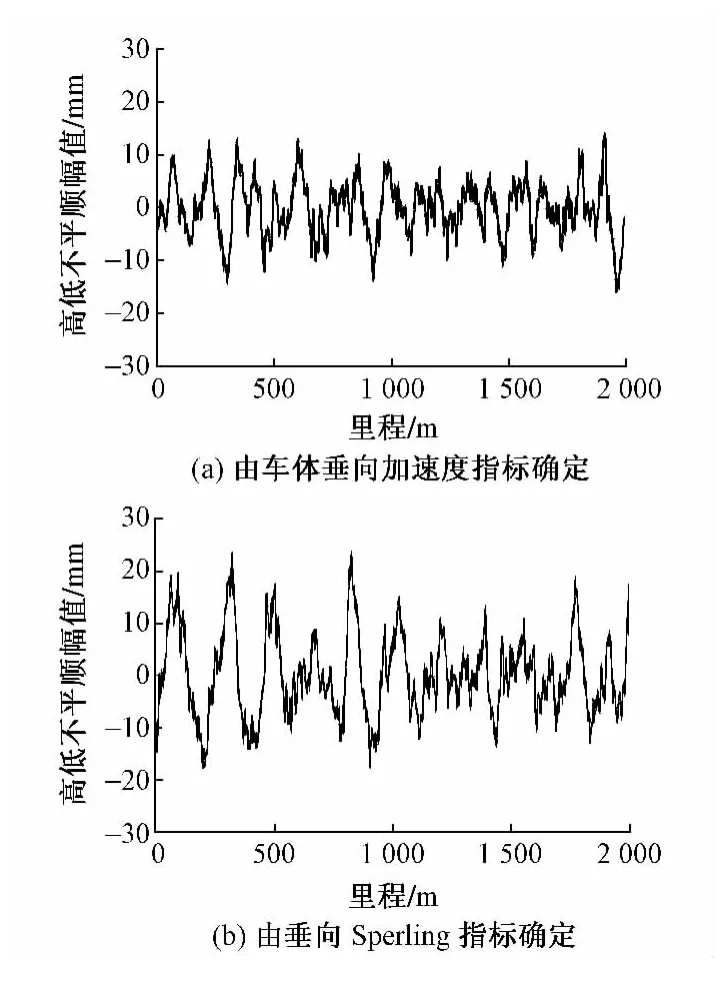
图5 武广谱限值模拟的时域不平顺样本
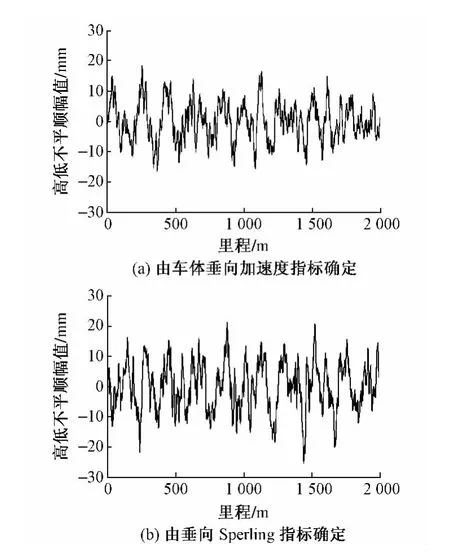
图6 德国谱限值模拟的时域不平顺样本
2.3 谱限值校核
利用数值模拟方法分别将上述谱限值分别转换成1 000组,每组有2 km长的时域不平顺样本,计算了车体心盘处垂向振动加速度时域响应,与频域计算结果进行对比。
在Slimit_VCA(ω)激扰下,时域、频域车体心盘处垂向振动加速度均方根值如图7所示,频域均方根值根据车体垂向振动加速度指标限值(0.13g)运用3σ规则确定。由图可见,时域均方根值都在相应频域均方根值附近波动,且时域、频域偏差均<7%,二者均方根值十分接近。

图7 轨道谱限值激扰下的车体垂向加速度均方根
对于武广谱和德国谱,在各自Slimit_VCA(ω)激扰下的车体心盘处垂向振动加速度超过其指标限值0.13g的概率分别为0.23%和0.25%,均略小于3σ规则预测的双侧概率0.26%,由此说明,谱限值激扰下的车体心盘处垂向振动加速度 >0.13g的可能性很小,满足车辆垂向加速度指标限值。
对各样本计算得到的车体心盘处垂向振动加速度时域响应,利用式(12)计算各样本垂向Sperling指标,并对其进行平均。对于武广谱和德国谱,平均后的Sperling指标值分别为2.52和2.53,与 Sperling指标限值2.5十分接近,说明频域估计的Sperling指标正确,反映出由 Sperling指标估计的谱限值 Slimit_W(ω)合理。
综合以上分析,对于武广谱和德国谱,在由车体垂向加速度指标限值确定的谱限值Slimit_VCA(ω)激扰下,车体垂向加速度时域响应能够满足其指标限值;在由垂向Sperling指标确定的谱限值Slimit_W(ω)激扰下,时域平均Sperling指标与频域模型计算结果十分接近。由此说明,应用本文提供的方法进行轨道高低不平顺谱限值估计是合理可靠的。
3 结论
通过建立车辆—轨道垂向耦合动力学频域模型,运用平稳随机过程理论,提出了一种根据舒适性指标估计轨道高低不平顺谱限值的方法。采用该方法,以我国武广客运专线和德国低干扰轨道高低不平顺谱为例,对350 km/h行车速度下的谱限值进行了估计。对于武广谱和德国谱,根据车体垂向振动加速度指标估计的谱限值对应的高低不平顺最大值分别为20.0 mm和19.4 mm,根据车体垂向Sperling指标估计的谱限值对应的高低不平顺最大值分别为24.1 mm和24.2 mm;由车体垂向加速度指标确定的谱限值均较由Sperling指标确定的谱限值低;时域模型计算结果表明,在各谱限值激扰下,其对应舒适度指标值均与频域模型计算的指标值相吻合,从而说明了本文提出的谱限值估计方法的正确性。分析方法及相关研究结果可为高速铁路轨道不平顺管理提供参考。
应当指出的是,本文侧重研究高低不平顺谱限值的估计方法,关于谱限值的具体确定,尚需同时考虑其它几种轨道不平顺的共同作用,根据中国高速铁路车辆运营状况及线路状态等条件,开展更为深入和广泛的研究。
[1]陈宪麦.轨道不平顺时频域分析及预测方法的研究[D].北京:中国铁道科学研究院,2006.
[2]中国铁道科学研究院.既有线轨道不平顺谱的研究[R].北京:中国铁道科学研究院,2007.
[3]罗文灿,朱开明,罗林.干线轨道不平顺速度管理标准建议值的研究[J].中国铁道科学,1994,15(1):82-100.
[4]蔡成标,翟婉明,王其昌.轨道几何不平顺安全限值的研究[J].铁道学报,1995,17(4):82-87.
[5]陈果,翟婉明,左洪福.250 km/h高速铁路轨道不平顺的安全管理[J].西南交通大学学报,2001,36(5):495-499.
[6]吴旺青.秦沈客运专线300 km/h综合试验段轨道不平顺管理标准建议值的研究[J].铁道标准设计,2003(4):1-4.
[7]GAO J M,ZHAI W M.Effect of Track Irregularity Amplitude on Dynamic Performance of Vehicle System under High-speed Operation[C]//Proceedings of Fifth International Symposium on Environmental Vibration.Beijing:Science Press,2011:667-673.
[8]翟婉明.车辆—轨道耦合动力学[M].3版.北京:科学出版社,2007.
[9]陈果.车辆—轨道耦合系统随机振动[D].成都:西南交通大学,2000.
[10]陈果,翟婉明.铁路轨道不平顺随机过程的数值模拟[J].西南交通大学学报,1999,34(2):138-142.
[11]中华人民共和国铁道部.GB 5599—85 铁道车辆动力学性能评定和试验鉴定规范[S].北京:中国计划出版社,1985.
[12]林家浩.随机振动的虚拟激励法[M].北京:科学出版社,2004.
[13]盛骤,谢式千,潘承毅.概率论与数理统计[M].4版.北京:高等教育出版社,2010.
[14]中华人民共和国铁道部.TB 10621—2009 高速铁路设计规范(试行)[S].北京:中国铁道出版社,2009.
[15]中国铁道科学研究院.武广客运专线轨道不平顺谱和轮轨关系试验研究[R].北京:中国铁道科学研究院,2009.
U238;U216.3
A
10.3969/j.issn.1003-1995.2013.09.33
1003-1995(2013)09-0104-05
2013-02-15;
2013-06-20
国家“九七三”计划项目(2013CB036205);国家自然科学基金高铁联合基金项目(U1234209)
田国英(1986— ),男,陕西渭南人,博士研究生。
(责任审编 王 红)

